Trägheitsschwingung

Die Trägheitsschwingung, auch Inertialschwingung genannt, ist eine charakteristische instationäre Bewegungsform des Wassers in einem unbegrenzten Ozean auf der rotierenden Erde, die durch das Gleichgewicht von Trägheitskraft und Corioliskraft bestimmt ist. Die Trägheitsschwingung ist der Spezialfall der Poincaré-Welle mit unendlich großer Wellenlänge.

Seit Gustafson und Otterstedt 1932 erstmals Trägheitsschwingungen in der Ostsee beobachteten, wurden sie in fast allen Ozeanen und Randmeeren nachgewiesen.

Eigenschaften

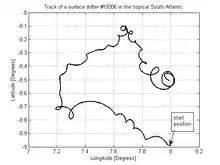
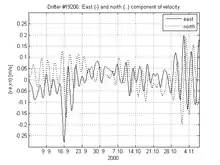
Bahn eines Oberflächendrifters im tropischen Südatlantik (Gegenuhrzeigersinn), geformt durch geostrophische und windgetriebene Strömungen sowie durch Trägheitsschwingungen

Geschwindigkeitskomponenten eines Oberflächendrifters im tropischen Südatlantik zwischen 8° und 9°S. Die lokale Trägheitsperiode beträgt 3,1 Tage.

In der oberflächennahen Schicht des Ozeans (z > -h) rotiert der resultierende Geschwindigkeitsvektor, sprungförmig beginnend mit t = 0, mit konstantem Betrag, auf der Nordhalbkugel im Uhrzeigersinn und auf der Südhalbkugel im Gegenuhrzeigersinn, mit folgender Kreisfrequenz, die auch Coriolisparameter genannt wird:

f_{C}={\frac {2\cdot \pi }{T_{i}}}=2\cdot \Omega \cdot \sin \varphi

Dabei ist

$\Omega$ die Winkelgeschwindigkeit der Erdrotation
$\varphi$ der Breitengrad
T_i die Trägheitsperiode (Periode der Trägheitsschwingung):

T_{i}={\frac {2\cdot \pi }{2\cdot \Omega \cdot \sin \varphi }}

Die Wasserteilchen in der oberflächennahen Schicht bewegen sich auf Kreisen mit dem Radius

R={\frac {u_{0}}{f_{C}}}

Die charakteristischen Geschwindigkeiten haben in weiten Teilen des Ozeans die Größenordnung

u_{0}={\mathcal {O}}(10^{-1}\,{\rm {{m/s})}}

In den mittleren Breiten hat der Coriolisparameter die Größenordnung

{\begin{aligned}f_{C}&={\mathcal {O}}(10^{-4}\,1/s)\\\Rightarrow R&={\mathcal {O}}(1\,{\rm {{km})}}\end{aligned}}

In tropischen Breiten dagegen ist der Coriolisparameter eine Größenordnung kleiner, der Trägheitsradius beträgt daher dort 10 km.

Der tiefe Ozean unterhalb von z←H verbleibt in Ruhe, da die Oberflächenströmung frei von Divergenzen ist und somit keine horizontalen Druckgradienten aufgebaut werden, die die tiefen Schichten in Bewegung setzen können.

Mathematische Beschreibung

Hier sei ein einfaches Beispiel betrachtet: das Wasser in der oberen Schicht des Ozeans wird zum Zeitpunkt t = 0 auf die Geschwindigkeit u₀ beschleunigt, und zwar gleichförmig von der Oberfläche z = 0 bis zur Tiefe z = −h durch einen plötzlichen Impuls großmaßstäblich, d. h. räumlich konstant, nach Osten. Großmaßstäblich bedeutet, dass der anregende Impuls über ein Gebiet mit einem Durchmesser von wesentlich mehr als einem Rossby-Radius konstant sein muss.

Die Bewegungsgleichungen für die Wasserteilchen lauten dann, unter Vernachlässigung der Reibung:

{\frac {du}{dt}}-f_{C}\cdot v=u_{0}\cdot \Theta (z+h)\cdot \delta (t)

{\frac {dv}{dt}}+f_{C}\cdot u=0

mit

u, v die Geschwindigkeitskomponenten nach Osten und Norden
$\Theta$ der Verdrehwinkel
δ(t) die Dirac’sche Deltafunktion.

Die Komponenten der Geschwindigkeit haben dann folgenden Verlauf:

u(t)=\Theta (t)\cdot u_{0}\cdot \Theta (z+h)\cdot \cos(f_{C}\cdot t)

v(t)=-\Theta (t)\cdot u_{0}\cdot \Theta (z+h)\cdot \sin(f_{C}\cdot t)

Beobachtungen und Vorkommen

Werden Trägheitsschwingungen in begrenzten Meeren angeregt, so entstehen an den Küsten zwangsläufig divergente Strömungen, da die Strömung hier nicht senkrecht zur Küste gerichtet sein kann. Die dabei entstehenden Druckgradienten regen unter anderem eine barotrope Poincaré-Welle an, die von der Küste in den Ozean abstrahlt. Dabei stellt sich hinter der Wellenfront eine Strömung ein, die die mit den Trägheitsschwingungen verbundenen Wasserbewegungen derart modifiziert, dass der Wassertransport der gesamten Wassersäule senkrecht zum Ufer null ist. Durch die Poincaré-Welle wird somit der tiefe Ozean in Bewegung gesetzt.

Die Front der barotropen Poincaré-Welle breitet sich von der Küste mit der Geschwindigkeit $c={\sqrt {gH}}$ in den Ozean aus, so dass selbst im Stillen Ozean in der Größenordnung von einem Tag die Wellenfront das gegenüber liegende Ufer erreicht. Praktisch kann somit eine reine Trägheitsschwingung in der Deckschicht auf der Erde nur über maximal eine Trägheitsperiode existieren. Danach ist auch der tiefe Ozean in eine zur Oberflächenschicht gegenläufige Bewegung gesetzt. Die Bewegung in der Tiefenschicht ist im Ozean im Allgemeinen sehr schwach, da sich ihre Amplitude zur Amplitude der Deckschicht verhält wie ${\frac {h}{H-h}}$ , wenn H die Wassertiefe des Ozeans ist.

Siehe auch

Ekman-Transport

Literatur

T. Gustafson, B. Otterstedt: Observations de courants dans la Baltique 1931. Svenska Hydrografisk-Biologiska Kommissionens Skrifter, Serie Hydrografi XIII. 1932. S. 3–14

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.