Skalenertrag
Der Begriff der Skalenerträge (auch Niveaugrenzprodukt, engl. returns to scale) ist ein Bestandteil der Produktionstheorie. Im Gegensatz zu den Skaleneffekten geben die Skalenerträge die Rate an, mit der sich eine auf wenigstens zwei Produktionsfaktoren beruhende Produktion bei proportionaler Erhöhung aller Produktionsfaktoren erhöht.
Begriffsklärung
Die Begriffe des Skalenertrags und des Skaleneffekts werden in der Produktionstheorie der Betriebswirtschaftslehre und in der Mikroökonomie als die Abhängigkeit der Produktionsmenge von der Menge eingesetzter Produktionsfaktoren definiert.
Die Skalenerträge geben die Steigerungsrate an, mit der sich der Output bei proportionaler Erhöhung des Inputs erhöht.[1] Sie zeigen an, wie die Produktionsmenge reagiert, wenn alle Faktoren bei unverändertem Einsatzverhältnis vermehrt eingesetzt werden. Skalenerträge sind eine Eigenschaft der Produktionsfunktion.
Skaleneffekte hingegen sind die Effekte, die aus steigenden oder fallenden Skalenerträgen heraus resultieren.
In dem Zusammenhang der Skalenerträge gibt es noch weitere Begriffe, die sich sehr ähneln, jedoch voneinander abzugrenzen sind. Hier ist vor allem der Begriff des Verbundeffekts (Verbundvorteile) zu nennen.
Arten von Skalenerträgen
Konstante Skalenerträge
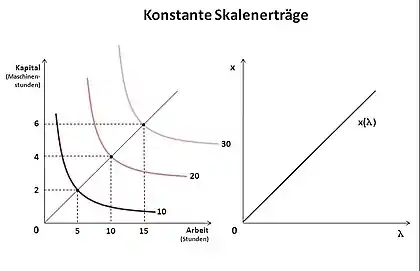
Von konstanten Skalenerträgen (constant returns to scale) spricht man, wenn bei einer proportionalen Veränderung der Einsatzfaktoren um einen Faktor a auch der Output um den Faktor a ansteigt. Es gilt:
Bei konstanten Skalenerträgen ist die Produktionsfunktion homogen vom Grad 1.
In der ersten Abbildung sind konstante Skalenerträge dargestellt. Es wird ersichtlich, dass für einen Output von zehn Einheiten ein Input von 2 Maschinenstunden () und fünf Arbeitsstunden () notwendig ist. Verdoppelt man nun den Input von zwei auf vier Maschinenstunden und von fünf auf zehn Arbeitsstunden erhält man unter der Voraussetzung konstanter Skalenerträge einen Output von 20 Einheiten. Die zweite Grafik stellt den linearen Verlauf und die Abhängigkeit des Outputs mit der Veränderung des Faktors a konstanter Skalenerträge dar. Beispiel:
- Bei den konstanten Skalenerträgen wird davon ausgegangen, dass in einem Unternehmen ein optimiertes Produktionsverfahren eingesetzt wird. Demzufolge kann man erwarten, dass ein zweites Unternehmen mit gleichem Produktionsverfahren den gleichen Output erzeugt. Nachvollziehbar wird diese Theorie am Beispiel eines Dienstleistungsunternehmens in der Stadt A.
- Für das Anbieten von Dienstleistungen benötigt das Unternehmen Kapital (Arbeitsplatz) und Arbeit (Sachbearbeiter/-in) um einen bestimmten Output (Service) zu erzeugen. Um den Output zu verdoppeln, wäre es denkbar, dass dieses Unternehmen den gleichen Service mit gleichem Verhältnis an Kapital und Arbeit in der Stadt B anbietet. Die Betriebsgröße spielt hierbei keine Rolle, da das Unternehmen für das Anbieten einer Dienstleistung, eine Sachbearbeiter/-in und diese einen Arbeitsplatz benötigt. Sollen zehn Dienstleistungen angeboten werden, benötigt das Unternehmen zehn Sachbearbeiter/-innen und zehn Arbeitsplätze. Bei konstanten Skalenerträgen beeinflusst somit die Betriebsgröße nicht die Produktivität der Einsatzfaktoren.
Die Annahme konstanter Skalenerträge ist jedoch nicht immer erfüllt. Dies ist der Fall, wenn bei der Verdopplung der Einsatzfaktoren ein effizienterer Einsatz dieser möglich wäre. D. h. bei Verdoppelung und effizienteren Einsatz der Einsatzfaktoren würden sich die Outputs mehr als verdoppeln. Auslöser hierfür könnte eine Spezialisierung und/oder Arbeitsteilung (z. B. durch die bessere Auslastung von Maschinen) sein. In diesem Fall spricht man von zunehmenden Skalenerträgen.
Zunehmende Skalenerträge
Zunehmende Skalenerträge (increasing returns to scale) liegen vor, wenn der Output um mehr als das a-fache zunimmt. Dann gilt:
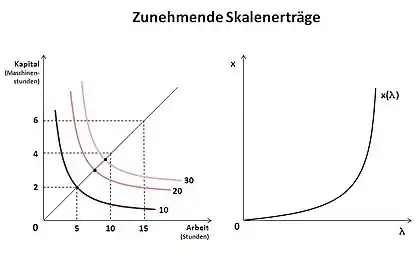
In der zweiten Abbildung sind die zunehmenden Skalenerträge dargestellt. Ausgangspunkt ist wieder ein Output von 10 Einheiten mit einem Input von 2 Maschinenstunden (x1) und 5 Arbeitsstunden (x2). Soll nun ein Output von 20 Einheiten erzeugt werden, benötigt man weniger als das Doppelte des Inputs. Vorliegend wird für ein Output von 20 Einheiten ein Input von 3 Maschinenstunden (x1) und 8 Arbeitsstunden (x2) benötigt. Erhöht man den Output auf 30 Einheiten, wird die Theorie der zunehmenden Skalenerträge deutlich. Es werden hierfür nur noch ca. 3,5 Maschinenstunden (x1) und ca. 9 Arbeitsstunden benötigt. Vergleicht man den Produktionsprozess mit dem der konstanten Skalenerträge, wird ersichtlich, dass man bei zunehmenden Skalenerträgen für einen Output von 30 Einheiten nahezu weniger als die Hälfte des Inputs benötigt. Der Abstand zwischen den Isoquanten nimmt mit steigender Outputmenge ständig ab. Grund hierfür ist das überproportionale Wachstum des Outputs bei proportionalem Faktoreinsatz a.
Die zweite Grafik kennzeichnet diesen Verlauf. Es gibt verschiedene Ursachen für zunehmende Skalenerträge:
- Vorteile aus der Arbeitsteilung, bei der komplexe Abläufe in einfache, leicht zu wiederholende Tätigkeiten zerlegt werden. Daraus resultierende Lernkurveneffekte tragen u. a. dazu bei, dass sich zunehmende Skalenerträge einstellen.
- Einsparungen durch die Verwendung größerer Produktionsmittel, wie z. B. größere Öfen und Tanks.[3]
- Hierbei ist anzumerken, dass nicht der Ofen den Skalenertrag hervorruft, sondern die größere Menge, die in einem größeren Ofen Platz hat.
- Rationalisierungen durch den Einsatz automatisierter Produktionsmittel (Roboter)
- Verwendung normierter Teile und zentralisierte Reservehaltung.
- Verbesserte Losgrößenabstimmung bei aufeinander folgenden Fertigungsstufen.
Abnehmende Skalenerträge
Abnehmende Skalenerträge (decreasing returns to scale) liegen vor, wenn der Ertrag nur unterproportional wächst. Dann gilt:
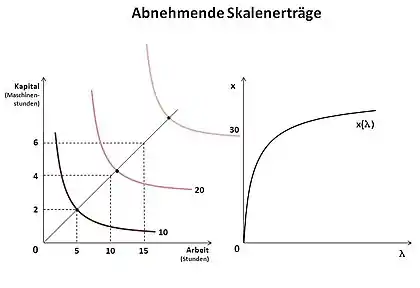
Die dritte Abbildung zeigt die abnehmenden Skalenerträge. Diese verhalten sich spiegelbildlich zu denen der zunehmenden Skalenerträge, die bereits im Vorfeld erläutert wurden. Im Wesentlichen gibt es zwei Ursachen für abnehmende Skalenerträge. Zum einen Verwaltungsprobleme bei zu großen Produktionsmengen und demzufolge auch zu großen Produktionsstätten. Zweitens geografische Faktoren. So kann beispielsweise der Standort einer zusätzlichen Produktionsstätte schlechter sein als der der bereits bestehenden Produktionsstätte.
Die abnehmenden Skalenerträge können am Beispiel einiger Unternehmen veranschaulicht werden, die in großem Umfang operieren. Bei solchen Unternehmen liegen die Schwierigkeiten darin, die Mitarbeiter zu leiten und zu organisieren. Erfüllt das Management diese Aufgaben nicht, werden die Mitarbeiter nicht effizient genug eingesetzt. Ein weiteres nicht unbedeutendes Problem großer Unternehmen ist zurückzuführen auf die interne Kommunikation. Daraus resultierend werden Arbeitsschritte doppelt oder sogar gar nicht ausgeführt. Der eingesetzte Input führt nicht zu dem gewünschten Ertrag.
Siehe auch
Literatur
- John Eatwell: returns to scale. In: Steven N. Durlauf und Lawrence E. Blume (Hrsg.): The New Palgrave Dictionary of Economics, Second Edition. 2008, doi:10.1057/9780230226203.1432.
- George J. Stigler: The Economies of Scale. The Journal of Law & Economics 1 (1958): S. 54–71. www.jstor.org/stable/724882.
Einzelnachweise
- Robert S. Pindyck, David L. Rubinfeld: Mikroökonomie. 5. Auflage. Pearson Studium, München 2003, S. 289.
- Hanusch, Kuhn, Canter: Volkswirtschaftslehre. Bd. 1: Grundlegende Mikro- und Makroökonomik. 6. Auflage. Springer Verlag, Berlin 2002, S. 173
- Varian: Mikroökonomie. 3. Auflage. Oldenbourg, ISBN 3-486-22483-2, S. 15–16