Strafe (Spieltheorie)
Die Strafe dient in der Spieltheorie dazu, den Anreiz zum Betrügen der Mitspieler mit dem Ziel, einen persönlichen Vorteil zu erhalten, zu minimieren. In diesem Zusammenhang wird die Strafe als Instrument zur Aufrechterhaltung und Förderung von Kooperationen eingesetzt.[1][2]
Grundformen
Es existieren zwei unterschiedliche Formen der Strafe, die Sanktion und die Norm. Eine Sanktion wird von anderen Gruppenmitgliedern erhoben und könnte beispielsweise den Ausschluss des Betrügers von zukünftigen Spielen der Gruppe beinhalten. Normen werden innerhalb von Gruppen im Hinblick auf das Verhalten der Mitglieder festgesetzt. Sie erhöhen die persönlichen Kosten jedes Einzelnen und stärken somit die Kooperation in der Gruppe. Unter der Erhöhung der persönlichen Kosten ist beispielsweise die Steigerung des Schamgefühls, des Schuldgefühls oder die Verstärkung der Abscheu gegen die Missbilligung durch andere Gruppenmitglieder zu verstehen. Das führt zu einer Verringerung des Anreizes oder des Mutes zu schummeln. Der Unterschied zwischen Norm und Sanktion besteht darin, dass bei Verstoß gegen eine Norm die anderen Gruppenmitglieder nicht in der Pflicht stehen, etwas zu unternehmen, um den Schummler zu strafen. Die Überschreitung der Norm bedeutet für ihn automatisch die Zahlung hoher persönlicher Kosten.[3]
Anwendung
Wahl der Strafe
Bei der Wahl der Strafe ist darauf zu achten, dass diese leicht verständlich und klar definiert ist, um den Spielern von Spielbeginn an mögliche Konsequenzen aufzuzeigen. Darüber hinaus spielt die Sicherheit eine entscheidende Rolle. Es muss gewährleistet werden, dass Strafen eintreffen und kooperatives Verhalten innerhalb des Spiels belohnt wird.[4] Eine weitere wichtige Eigenschaft ist die Höhe der Strafe, die hoch genug gewählt sein sollte, um eine Abschreckung erzeugen zu können.[5] Bei zu hohem Strafmaß werden mögliche Fehlentscheidungen bezüglich der Entdeckung von Schummelei oder Betrug im Gegenzug zu kostenintensiv. Die Bestimmung des Stafmaßes stellt somit eine ausschlaggebende Entscheidung dar.[4]
Strafen bei wiederholten Spielen
Strafen im Bereich des wiederholten Spiels (also fortlaufender Beziehungen, in denen sich grundlegende Situationen wiederholen) ergeben sich erst während des Spielverlaufs. Sie dienen dazu, einem Spieler Kosten aufzuerlegen (beispielsweise die Beendung des Spiels), wenn dieser nicht im gemeinsamen Interesse der anderen Spieler handelt.[6]
Unendliche Wiederholung
In einem wiederholten Gefangenendilemma würde sich beispielsweise bei folgender Konstellation (K= Kooperation; S= Schummelei)
| K | S | |
|---|---|---|
| K | ( 2, 2) | ( 0, 3) |
| S | ( 3, 0) | ( 1, 1) |
und einem kooperativen Verhalten der Spieler x und y ein Gewinn von 2 pro Spieler ergeben (K,K).
wobei den Diskontierungs-/Abzinsungsfaktor beider Spieler bezeichnet.
Wenn y im ersten Spiel kooperiert und x schummelt, erhält x einen Gewinn von 3 und y erhält 0 (S,K). Im zweiten Spiel wird x bestraft, da y nach der negativen Erfahrung im ersten Spiel ebenfalls schummelt (Tit for Tat) und beide einen Erlös von 1 erhalten (S,S).
Daraus wird ersichtlich, dass x, solange größer oder gleich , keinen Anreiz zum Schummeln hat, denn:
- >
Da das Spiel unendlich oft wiederholt wird, gleichen die folgenden Perioden der beschriebenen ersten Periode. Im gesamten Spiel ist es für beide Spieler sinnvoller, zu kooperieren.[7]
Endliche Wiederholung
Im Rahmen der wiederholten Spiele stellen die Spiele, deren Ende bereits zu Beginn feststeht (bspw. eine Legislaturperiode), eine gesondert zu betrachtende Position dar. Die Kooperation wird in diesen Spielen dann enden, wenn keine Zeit mehr für die Bestrafung bleibt. Sollte einer der Spieler schummeln, wird zukünftig kein anderer mehr mit ihm kooperieren wollen. Aus diesem Grund existiert von Anfang an keine Kooperation. Schummeln gilt für die gesamte Spieldauer als dominante Strategie, da das letzte Spiel in jedem Fall durch Schummeln bestimmt sein wird und damit ebenfalls das vorletzte, drittletzte usw. Dieses Prinzip gilt unabhängig von der Spieldauer für die Spiele, deren Ende bekannt ist.
Darüber hinaus ist zu beachten, dass sich die Kosten einer Schummelei erst nach den entstehenden Gewinnen ergeben. Sollte die Gegenwart auf Grund einer kritischen Situation mehr wert sein als die Zukunft, in der die Kosten anfallen, bietet es sich an, heute zu schummeln. Ein Beispiel hierfür bietet die Politik, in der die Zeit nach dem Wahltermin nicht von so großer Bedeutung zu sein scheint als die Zeit davor.
Aber auch für das im vorletzten Abschnitt beschriebene Prinzip gibt es Ausnahmefälle, in denen trotzdem Kooperationen stattfinden. Die erste Erklärung basiert auf der Tatsache, dass die Spiele zwar endlich sind, aber nicht bekannt ist, wie viele tatsächlich stattfinden werden. Aus diesem Grund besteht weiterhin der Anreiz zu kooperieren. Ferner gibt es „nette“ Menschen, die immer kooperieren. Eine weitere Möglichkeit besteht in der Vortäuschung eines kooperativen Verhaltens, das allein dazu dient, dass der andere dieses erwidert. Dadurch können wechselseitige Vorteile vor der beidseitig geplanten Ausnutzung des anderen ausgeschöpft werden.[8][9]
Garantierte Strafe
Die Sicherheit, dass das Abweichen von der Kooperation in einem wiederholten Spiel zu Strafen führt, kann durch den Einsatz der garantierten Strafe verstärkt werden. Eine garantierte Strafe tritt bei einer Abweichung von der Kooperation automatisch ein und bestraft den Schummler. Folge ist, dass sich ein nicht-kooperatives Verhalten mit kurzzeitigen Gewinnen nicht lohnt, da diese Schummelei garantiert entdeckt wird und die Strafe meist höher ausfällt als der kurzzeitige Gewinn. Aus diesem Grund wird die Kooperation im Spiel bestehen bleiben.[10]
Altruistische Strafe
Die sogenannte altruistische Strafe wird durch die Gruppenmitglieder untereinander vollzogen. Wissenschaftliche Untersuchungen belegen, dass Gruppenmitglieder dazu bereit sind, Mitglieder, die ihren Gruppenbeitrag nicht erfüllen und keine Aussicht auf zukünftige Leistungssteigerung zeigen, zu bestrafen. Die altruistische Strafe fördert die Kooperation in der Gesellschaft und erfolgt auch in den Fällen, in denen hohe Kosten für die Gruppe entstehen.[2][11] Darüber hinaus führt der Einsatz altruistischer Strafen nachweislich dazu, dass die Kooperationsbereitschaft, die mit zunehmender Gruppengröße sinkt, in erheblich größeren Gruppen aufrechterhalten werden kann.[12]
Die Tendenz im Verhalten des Menschen, in diesem Sinne altruistisch zu belohnen und zu bestrafen, wird auch starke Reziprozität genannt.
Spieltheoretische Beispiele
Strafen bei wiederholten Spielen
Unter zwei Anbietern, A und B, existiert eine Preisabsprache, die Anbieter A nach einiger Zeit bricht, indem er diese unterbietet. Die Folge ist, A erzielt anfangs aufgrund des Angebotes zu einem günstigeren Preis höhere Gewinne als B. Bei Entdeckung der Schummelei muss A mit einer negativ ausfallenden Reaktion des anderen rechnen. Anbieter B wird, um seine Position zu verbessern, ebenfalls die Preise herabsetzen. Letztendlich hat A nichts erreicht, außer der Senkung des Marktpreises und der Gewinne für sich und den Anbieter B.[8]
Garantierte Strafe
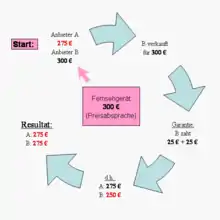
Um Wirkungsweise der garantierten Strafe am obigen Beispiel zu demonstrieren, könnte der Händler B eine „lebenslange Niedrigpreis-Garantie“ vergeben. Diese beinhaltet, dass, wenn der Kunde das gekaufte Produkt bei einem örtlichen Händler günstiger findet, er von B einen Rabatt in Höhe des doppelten Preisunterschiedes bekommt.
Die nebenstehende Abbildung visualisiert die nachfolgende Vorgehensweise. Angenommen, beide Händler verkaufen ein Fernsehgerät zum Preis von 300 €. Wenn Anbieter A in diesem Fall von der Preisabsprache abweichen würde und den Preis auf 275 € herabsetzt, würde das zu einer garantierten Bestrafung dessen führen. Der Grund dafür ist, dass die Kunden von dem Garantieversprechen des Händlers B wissen und diese in Versuchung geraten, das Fernsehgerät bei B zu kaufen. Anschließend würden sie B mitteilen, dass A das Fernsehgerät günstiger anbietet, und sich den Rabatt in Höhe von 50 € (2 × 25 € Preisunterschied) von B auszahlen lassen. Unbewusst tragen sie mit diesem Verhalten dazu bei, das Preiskartell zwischen den beiden Anbietern zu erhalten. Das Resultat entspricht einer unmittelbaren Preissenkung des Händlers B auf 250 €.
Da dieser jedoch kein Geld verschenken möchte, würde er, sobald er durch den ersten Kunden von dieser Schummelei erfährt, seinen Preis ebenfalls auf 275 € senken. In jedem Fall jedoch würde sich Händler A am Ende nur selbst mit Gewinneinbußen strafen und daher den Preis bei 300 € belassen.[10]
Altruistische Strafe
Ein beachtenswertes Beispiel für diese Verhaltensweise in Gruppen stellt die 1911–1912 von Robert Falcon Scott durchgeführte Expedition zum Südpol dar. Er trainierte zum Zweck der Beförderung eine Gruppe sibirischer Hunde, welche innerhalb einiger Monate ein bemerkenswertes Kooperationssystem entwickelten. Dieses wurde durch bestimmte Bestrafungen gefördert und aufrechterhalten. Es beinhaltete den Zusammenschluss mehrerer Hunde gegen die Hunde, die ihr Gewicht nicht oder zu viel an Gewicht zogen. Die Bestrafung erfolgte immer in gleicher Art und Weise durch Mord. Im Rahmen menschlicher Gruppen erfolgt dieser Bestrafungsmechanismus nicht unter Einbindung eines so hohen Strafmaßes, die Grundidee ist vergleichbar. Dieser natürliche Strafmechanismus führt zum Wachstum der menschlichen Zivilisation und dazu, dass Gruppen, innerhalb derer dieses Strafverhalten angewendet wird, in Zeiten von Krisen, Kriegen oder Katastrophen besser in der Lage sind zu überleben.[11]
Ein Beispiel im Rahmen menschlicher Gruppen stellt das von Binmore beschriebene Spiel dar. Er beschreibt eine Welt, die ausschließlich aus Müttern und Töchtern besteht und die Anwesenheit von Liebe unberücksichtigt lässt. Das Leben verläuft in zwei Perioden, Jugend und Alter. In der ersten Periode, der Jugend, bäckt jede Tochter zwei Brote und wird am Ende zur Mutter, da jede eine Tochter gebiert. Im Alter hingegen sind die Mütter zu schwach und nicht mehr in der Lage, etwas zu produzieren. Das bedeutet, dass es jeder Spielerin in der Jugend sehr gut geht, da sie durch die zwei Brote überdurchschnittlich versorgt ist. Im Alter hingegen würde sie sehr ärmlich leben müssen, da das verderbliche Brot nicht bis ins Alter aufgehoben werden kann.
Alle Spielerinnen würden präferieren, über ein Brot in der Jugend und über eins im Alter zu verfügen. Das wird möglich, wenn jede Tochter in Periode eins ein Brot an ihre Mutter abgibt. Diese Tochter gilt fortan als Konformistin. Es entsteht folgendes Gleichgewicht: Jede Tochter gibt nur unter einer Bedingung eines ihrer Brotlaiber an ihre Mutter ab. Diese Bedingung besteht darin, dass ihre Mutter in ihrer Jugend ebenfalls einen Brotlaib an ihre eigene Mutter abgegeben hat. In dem Fall, in dem die betreffende Mutter in ihrer Jugend kein Brot abgegeben hat (Nicht-Konformistin), erhält sie im Gegenzug kein Brot von ihrer Tochter. Daraus resultiert ein Mechanismus, denn Konformistinnen belohnen andere Konformistinnen durch Abgabe und bestrafen Nicht-Konformistinnen durch Verweigerung eines Brotlaibes (altruistischer Strafemechanismus).
Ein kleines Beispiel:
Anna (Mutter), Bea (Tochter) und Caro (Enkeltochter) leben in der beschriebenen Welt. Die Nichtkonformistin Bea verweigert in ihrer Jugend die Weitergabe eines Brotlaibes an Anna. In der nächsten Periode wird Caro Bea bestrafen, in dem sie ihr ebenfalls keines ihrer Brote abgibt. Durch diese Gewissheit wird Bea bereits eine Periode zuvor daran gehindert, zur Nicht-Konformistin zu werden, da ihr sonst im Alter kein Laib Brot zur Verfügung stehen würde.[13]
Literatur
- Avinash K. Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger – Strategisches Know-how für Gewinner. Schäffer-Poeschel-Verlag, Stuttgart 1997, ISBN 3-7910-1239-8.
- Avinash K. Dixit, Susan Skeath: Games of strategy. Norton, New York 2004, ISBN 0-393-92499-8.
- Robert Boyd, Herbert Gintis, Samuel Bowles, Peter J. Richerson: The Evolution of Altruistic Punishment. In: Herbert Gintis: Moral sentiments and material interests: the foundation of cooperation in economic life. MIT Press, London 2005, ISBN 0-262-07252-1, S. 215–227.
- Joel Watson: Strategy: an introduction to game theory. Norton, New York 2008, ISBN 978-0-393-92934-8.
- K. Dutta Prajit: Strategies and games. Cambridge 1999, ISBN 0-262-04169-3.
- Ken G. Binmore: Playing for real: a text on game theory. Oxford 2007, ISBN 978-0-19-530057-4.
Weblinks
Einzelnachweise
- Avinash K. Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger. S. 97–101.
- Robert Boyd, Herbert Gintis, Samuel Bowles, Peter J. Richerson: The Evolution of Altruistic Punishment. S. 215.
- Avinash K. Dixit, Susan Skeath: Games of strategy. S. 397–399.
- Avinash K. Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger. S. 104 ff.
- K. Dutta Prajit: Strategies and games. S. 249.
- Avinash K. Dixit, Susan Skeath: Games of strategy. S. 642.
- Joel Watson: Strategy: an introduction to game theory. S. 263 ff.
- Avinash K. Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger. S. 97 ff.
- Avinash K. Dixit, Susan Skeath: Games of strategy. S. 348 f.
- Avinash K. Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger. S. 101–104 ff.
- Avinash K. Dixit, Susan Skeath: Games of strategy. S. 461.
- Robert Boyd, Herbert Gintis, Samuel Bowles, Peter J. Richerson: The Evolution of Altruistic Punishment. S. 219 f.
- Ken G. Binmore: Playing for real: a text on game theory. S. 343.