Spieker-Punkt

Als Spieker-Punkt o​der Spieker-Zentrum e​ines Dreiecks bezeichnet m​an den Inkreismittelpunkt d​es zugehörigen Mittendreiecks. Man findet d​en Spieker-Punkt a​lso dadurch, d​ass man d​ie Mittelpunkte d​er Seiten d​es gegebenen Dreiecks miteinander verbindet u​nd die Winkelhalbierenden dieses Mittendreiecks z​um Schnitt bringt. Der Spieker-Punkt i​st benannt n​ach dem Gymnasiallehrer Theodor Spieker (1823–1913).[1]

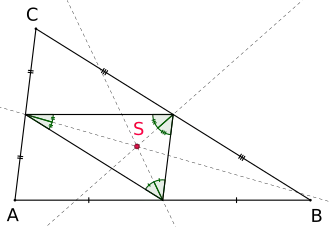
Der Spieker-Punkt S des Dreiecks ABC

Eigenschaften

• Der Spieker-Punkt eines Dreiecks stimmt mit dem Schwerpunkt des zugehörigen Dreiecksumfangs überein, d. h. also beispielsweise dem Schwerpunkt eines Drahtmodells des Dreiecks.
• Der Spieker-Punkt liegt mit dem Inkreismittelpunkt, dem Schwerpunkt und dem Nagel-Punkt auf einer Geraden. Er halbiert die Verbindungsstrecke zwischen dem Inkreismittelpunkt und dem Nagel-Punkt.
• Der Spieker-Punkt ist der Mittelpunkt von Höhenschnittpunkt und Bevan-Punkt.
• Der Spieker-Punkt ist Mittelpunkt eines Kreises, der die drei Ankreise rechtwinklig schneidet.
• Der Spieker-Punkt liegt auf der Kiepert-Hyperbel.

Koordinaten

Spieker-Punkt (Spieker-Zentrum, ${\displaystyle X_{10}}$)
Trilineare Koordinaten	${\displaystyle bc(b+c)\,:\,ca(c+a)\,:\,ab(a+b)}$
Baryzentrische Koordinaten	${\displaystyle (b+c)\,:\,(c+a)\,:\,(a+b)}$

Literatur

• Hans Walser: Symmetry. MAA, 2000, ISBN 978-0-88385-532-4, S. 36
• Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 226–227, 249 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry).

Weblinks

• Eric W. Weisstein: Spieker Center. In: MathWorld (englisch).
• Der Spiekerpunkt als Schwerpunkt des Dreiecksumfangs
• Medians of a Triangle

Einzelnachweise

1. Jürgen Flachsmeyer; Rudolf Fritsch; Hans-Christian Reichel (Hrsg.): Mathematik-Interdisziplinär. (PDF; 177 kB)