Bevan-Punkt

Der Bevan-Punkt gehört zu den ausgezeichneten Punkten eines Dreiecks. Er ist definiert als Mittelpunkt des Kreises, der durch die drei Ankreismittelpunkte des gegebenen Dreiecks geht. Die Bezeichnung Bevan-Punkt bezieht sich auf ein Problem, das der englische Mathematiker Benjamin Bevan im Jahre 1806 stellte und noch im gleichen Jahr von John Butterworth gelöst wurde.

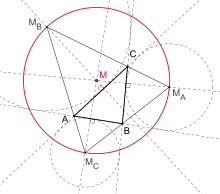
Bevan-Punkt M im Dreieck ABC

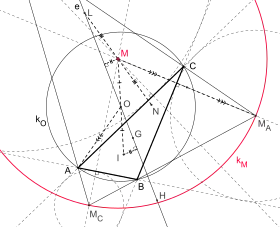
Bevan-Punkt M, Bevan-Kreis k_M, Höhenschnittpunkt H, Schwerpunkt G, Umkreismittelpunkt O, Inkreismittelpunkt I, Euler-Gerade e, Umkreis k_O

Eigenschaften

Die Verbindungsstrecken des Bevan-Punktes mit den Ankreismittelpunkten sind senkrecht zu den Seiten des gegebenen Dreiecks.
Die Verbindungsstrecke zwischen dem Bevan-Punkt und dem Inkreismittelpunkt des gegebenen Dreiecks wird durch den Umkreismittelpunkt des Dreiecks halbiert.
Der Bevan-Punkt ist der Mittelpunkt der Verbindungsstrecke von Nagel-Punkt und Longchamps-Punkt.
Die Verbindungsstrecke zwischen dem Bevan-Punkt und dem Höhenschnittpunkt wird durch den Spieker-Punkt halbiert.
Bevan-Punkt und Inkreismittelpunkt haben den gleichen Abstand d von der eulerschen Geraden, hierbei gilt $d={\sqrt {R^{2}-{\tfrac {abc}{a+b+c}}}}$
Die trilinearen Koordinaten betragen $(\cos \beta +\cos \gamma -\cos \alpha -1):(\cos \gamma +\cos \alpha -\cos \beta -1):(\cos \alpha +\cos \beta -\cos \gamma -1)$ .

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.