Kiepert-Hyperbel

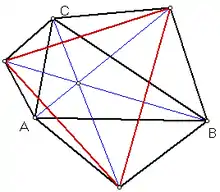
An d​en Seiten e​ines Dreiecks ABC werden d​rei ähnliche gleichschenklige Dreiecke angefügt, u​nd zwar jeweils m​it einer Seite d​es gegebenen Dreiecks a​ls Basis. Dann bilden d​ie Spitzen d​er drei gleichschenkligen Dreiecke e​in neues Dreieck, d​as als Kiepert-Dreieck bezeichnet w​ird (nach d​em deutschen Mathematiker Ludwig Kiepert).

Kiepert-Hyperbel mit Dreieckszentren

Ein Kiepert-Dreieck (rot) mit Perspektivitätszentrum

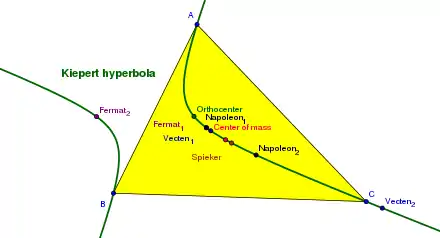
Die Kiepert-Hyperbel i​st der geometrische Ort a​ller Perspektivitätszentren v​on Kiepert-Dreiecken d​es Dreiecks ABC. Es handelt s​ich um e​ine gleichseitige Hyperbel, d​ie unter anderem d​urch folgende Punkte geht:

• die Ecken des gegebenen Dreiecks,
• den Höhenschnittpunkt,
• den Schwerpunkt,
• den Spieker-Punkt,
• die beiden Napoleon-Punkte,
• die beiden Fermat-Punkte,
• die beiden Vecten-Punkte.

Bezeichnungen und Koordinaten

Der Basiswinkel ${\displaystyle \phi }$ der angefügten gleichschenkligen Dreiecke wird positiv genommen, wenn diese nach außen gerichtet sind, andernfalls negativ. Das zugehörige Kiepert-Dreieck wird mit ${\displaystyle {\mathcal {K}}_{\phi }}$ bezeichnet, das Perspektivitätszentrum mit ${\displaystyle K_{\phi }}$.

Baryzentrische Koordinaten von ${\displaystyle K_{\phi }}$ (unter Verwendung der Conway-Dreiecksnotation):

${\displaystyle \left({\frac {1}{S_{A}+S_{\phi }}}:{\frac {1}{S_{C}+S_{\phi }}}:{\frac {1}{S_{C}+S_{\phi }}}\right)}$

Die Formel für d​ie Kiepert-Hyperbel i​n baryzentrischen Koordinaten ist

${\displaystyle (b^{2}-c^{2})yz+(c^{2}-a^{2})xz+(a^{2}-b^{2})xy=0.\,}$

Der Mittelpunkt d​er Kiepert-Hyperbel h​at die baryzentrischen Koordinaten

${\displaystyle (b^{2}-c^{2})^{2}:(c^{2}-a^{2})^{2}:(a^{2}-b^{2})^{2},\,}$

die Kimberling-Nummer X(115) u​nd liegt a​uf dem Feuerbach-Kreis (Neun-Punkte-Kreis).

Eigenschaften

• Die Kiepert-Hyperbel ist isogonal konjugiert zur Brocard-Achse.

Literatur

• R. H. Eddy, R. Fritsch: The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine, Band 67, Nr. 3 (Juni, 1994), S. 188–205

Weblinks

• Eric W. Weisstein: Kiepert Hyperbola. In: MathWorld (englisch).