Sphärenbündel

In der Mathematik sind Sphärenbündel Räume, die lokal wie ein Produktraum, dessen einer Faktor eine Sphäre ist, aussehen. Dazu gehören insbesondere Kreisbündel.

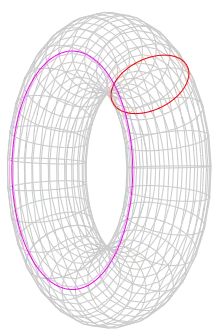
Ein Torus ist ein Produkt zweier Kreise und damit ein Kreisbündel über dem Kreis

Definition

Ein Sphärenbündel ist ein Faserbündel, dessen Faser eine Sphäre $S^{n}$ ist.

Für $n=1$ spricht man von einem Kreisbündel.

Beispiele

Das Einheits-Tangentialbündel einer differenzierbaren Mannigfaltigkeit ist ein Sphärenbündel.
Eine Produkt-Mannigfaltigkeit $M\times S^{n}$ ist ein (triviales) Sphärenbündel.
Der Torus und die Kleinsche Flasche sind Kreisbündel über dem Kreis.
Die Nichttrivialität eines Sphärenbündels wird durch seine Euler-Klasse gemessen, die wiederum in der Gysin-Sequenz Verwendung findet.

Literatur

Raoul Bott, Loring Tu: Differential forms in algebraic topology. Graduate Texts in Mathematics 82. Springer-Verlag, New York-Berlin, 1982. ISBN 0-387-90613-4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.