Sangaku
Sangaku (japanisch 算額, wörtlich ‚mathematische Tafeln‘) sind kunstvoll bemalte Holztafeln, die geometrische Aufgabenstellungen oder Rätsel zeigen. Sie wurden in Japan während der Edo-Zeit (1603–1867) von Angehörigen aller sozialen Schichten in Shintō-Schreinen und buddhistischen Tempeln aufgehängt. Dort dienten sie nicht nur als Opfergaben, sondern den nachfolgenden Pilgern auch als intellektuelle Herausforderung. Insofern spricht man auch von „Japanischer Tempelgeometrie“.
Geschichte

Die Sangaku entstanden während der Edo-Zeit, als Japan – von der westlichen Welt nahezu vollständig isoliert – eine eigene Mathematik-Tradition (japanisch: Wasan) entwickelte. Schon vor dem Aufkommen der Sangaku war es üblich, bemalte Holztafeln als Opfergaben in Tempeln aufzuhängen; sie zeigten – als Ersatz für ein teures Opfertier – dieses in bildlicher Darstellung. Die ersten Holztafeln mit geometrischen Motiven wurden vermutlich in der Mitte des 17. Jahrhunderts geschaffen. Heute geht man davon aus, dass zunächst die hochgebildeten Angehörigen der Samurai-Klasse die Urheber waren, dass aber zunehmend auch Bauern, Frauen und selbst Jugendliche Sangaku praktizierten. Insofern können die Sangaku der Unterhaltungsmathematik zugerechnet werden.
Auf den meisten Sangaku-Tafeln finden sich der Name des Herstellers und ein Datum. Die älteste heute noch erhaltene Tafel stammt aus dem Jahre 1683. Die Sangaku-Texte sind in Kanbun verfasst, d. h., sie wurden auf Japanisch in klassischem Chinesisch geschrieben, das heute von nur wenigen Menschen beherrscht wird. Viele Sangaku wurden im Laufe der Jahrhunderte – zusammen mit den Tempeln, die sie beherbergten – zerstört; heute sind aber noch mehr als 880, über ganz Japan verteilt, erhalten. Im Internet ist eine interaktive Karte verfügbar, die die Fundorte verzeichnet und Abbildungen der Tafeln zeigt.[1]
Die Erforschung der Sangaku wurde wesentlich von Hidetoshi Fukagawa, einem promovierten Mathematiker und Lehrer an einer höheren Schule, initiiert und vorangetrieben. Nachdem er 1969 auf das Thema gestoßen war und den heutigen Wert der Sangaku, etwa für den Schulunterricht, erkannt hatte, versuchte er (zunächst vergeblich), westliche Geometer für die im Westen noch gänzlich unbekannte Japanische Tempelgeometrie zu interessieren. Schließlich konnte er den britischen Mathematiker Daniel Pedoe für eine Zusammenarbeit gewinnen und gemeinsam veröffentlichten sie 1989 die erste englischsprachige Sangaku-Sammlung (siehe Literatur). Fukagawa, der Kanbun, die Sprache der Sangaku, für seine Forschung erst eigens erlernen musste, gilt heute als weltweit führender Sangaku-Experte.
Gegenstand

Die Aufgaben auf den Sangaku stammen überwiegend aus dem Bereich der klassischen euklidischen Geometrie. Sie befassen sich häufig mit einander berührenden Kreisen, Ellipsen und Dreiecken und unterscheiden sich deutlich von den geometrischen Aufgabenstellungen, wie sie an westlichen Schulen üblich sind. Die Sangaku zeigen nur die Problemstellungen und ggf. die finale Lösung, nicht aber den Lösungsweg im Detail. Insofern sind sie auch als intellektuelle Herausforderung an nachfolgende Tempelbesucher zu verstehen. Die an das Publikum gestellten Anforderungen sind sehr unterschiedlich: es gibt Aufgaben, die ein Student im ersten Semester lösen können sollte, und solche, denen ohne fortgeschrittene Methoden wie beispielsweise der affinen Transformation oder der Analysis kaum beizukommen ist. Nicht selten wurden auch Erkenntnisse westlicher Mathematiker vorweggenommen, so der Satz von Casey, die Malfatti-Kreise oder das Soddy-Hexlet. Auch die Steiner-Kette war bereits Thema eines Sangaku zu der Zeit, als Jakob Steiner diese in Europa postulierte.
Neben den geometrischen Fragestellungen thematisieren einige Sangaku auch nichtgeometrische Probleme wie diophantische Gleichungen oder die Berechnung der Volumina krummflächig begrenzter Körper.
Beispiele
Die beiden Diagramme zeigen zwei typische Sangaku-Problemstellungen; sie stammen aus der Präfektur Gunma aus den Jahren 1824 (Beispiel 1) bzw. 1803 (Beispiel 2).[3]
Beispiel 1

Drei einander berührende Kreise haben eine gemeinsame Tangente (horizontale schwarze Linie in der Abbildung). Gegeben seien die Radien der beiden äußeren, größeren Kreise (in der Abbildung hellblau und hellgrün); wie groß ist der mittlere (rosafarbene) Kreis? Gesucht wird das Verhältnis der drei Radien untereinander.
Die Antwort lautet:
Eine Herleitung findet sich in Hartmann: Sangaku – Japanische Tempelgeometrie, 2008.[4]
Beispiel 2
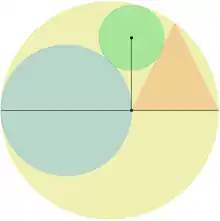
In einen Kreis (in der Abbildung der große, beigefarbene) wird eine horizontale Gerade (schwarz) durch seinen Mittelpunkt eingezeichnet. Ein gleichschenkliges Dreieck sitzt mit seiner Basis auf dieser Geraden, seine Spitze und der rechte Basis-Eckpunkt liegen auf dem Kreis. Der Mittelpunkt eines weiteren Kreises (hellblau) liegt ebenfalls auf der Geraden; dieser Kreis berührt den großen Kreis von innen und geht durch den linken Basis-Eckpunkt des Dreiecks. Ein dritter Kreis (grün) wird nun so einbeschrieben, dass er den großen Kreis von innen und den kleineren, blauen Kreis und das Dreieck von außen berührt.
Aufgabe: Beweise, dass die Verbindung des Mittelpunktes des grünen Kreises mit dem Berührpunkt zwischen dem blauen Kreis und dem Dreieck senkrecht auf der horizontalen Geraden steht.
Eine mögliche Beweisführung beschreibt Ingmar Rubin auf www.matheraetsel.de.[5]
Beispiel 3
Von einer Sangaku-Tafel aus dem Jahre 1743 stammt folgendes Rätsel[6] (ein Beispiel für eine nichtgeometrische Aufgabenstellung): 50 Tiere – Hasen und Hühner – haben zusammen 122 Füße. Um wie viele Hasen und wie viele Hühner handelt es sich?
Siehe auch
Einzelnachweise
- Hiroshi Kotera: Japanese Temple Geometry Problem. www.wasan.jp, abgerufen am 2. Juli 2013.
- Fukagawa, Rothman: Sacred Mathematics, 2008. S. 83
- Rothman, Fukakawa: Japanese Temple Geometry, 1989, S. 86 ff, 91.
- Christiane Hartmann: Sangaku – Japanische Tempelgeometrie. (MS Word; 3,3 MB) Hausarbeit zum Staatsexamen. Julius-Maximilians-Universität Würzburg, 2008, S. 25–27, abgerufen am 2. Juli 2013.
- Ingmar Rubin: Sangaku-Probleme. (PDF; 195 kB) www.matheraetsel.de, S. 30 f, abgerufen am 2. Juli 2013.
- Fukagawa, Rothman: Sacred Mathematics, 2008. S. 92.
Literatur
- Hidetoshi Fukagawa, Tony Rothman: Sacred Mathematics – Japanese Temple Geometry. Princeton University Press, Princeton und Oxford 2008, ISBN 978-0-691-12745-3.
- Hidetoshi Fukagawa, Daniel Pedoe: Japanese Temple Geometry Problems – San Gaku. Charles Babbage Research Foundation, Winnipeg, Canada 1989, ISBN 978-0-919611-21-4.
- Tony Rothman, Hidetoshi Fukagawa: Japanese Temple Geometry. In: Scientific American. Mai 1989, S. 84–91. (online, kostenpflichtig)
- Hidetoshi Fukagawa, Tony Rothman: Sangaku: Japanische Geometrie. In: Spektrum der Wissenschaft. Nr. 7, 1998, S. 80. (online, kostenpflichtig)
Weblinks
- Ingmar Rubin: Sangaku-Probleme (PDF; 195 kB) auf www.matheraetsel.de (Beispiele mit Lösungen)
- Beispielaufgabe mit Lösung im Archimedes' Laboratory (englisch)
- Hiroshi Okumura Japanese Mathematics (PDF; 258 kB) (Memento vom 13. Juli 2007 im Internet Archive)
- Christiane Hartmann: Sangaku – Japanische Tempelgeometrie (MS Word; 3,3 MB). Hausarbeit zum Staatsexamen. Julius-Maximilians-Universität Würzburg. 2008
- Sangaku: Mathetest als Opfergabe auf https://kawaraban.de
