E-Kurve
Die E-Kurve[1] zählt zur Gruppe der so genannten FASS-Kurven (space-filling, self-avoiding, simple, self-similar). Diese Kurven sind raum- bzw. flächenfüllend, selbstausweichend (d. h. überschneidungs- und berührungsfrei), einfach und selbstähnlich.
Durch Wiederholung ihres Konstruktionsverfahrens, bei dem jedes einzelne Segment des Linienzuges durch ein verkleinertes Abbild des gesamten Linienzuges ersetzt wird, kommt die E-Kurve nach einer ausreichenden Anzahl von Konstruktionsschritten jedem beliebigen Punkt einer quadratischen Fläche beliebig nahe ohne sich selbst zu schneiden. Der Grenzwert dieser unendlichen Folge selbstähnlicher Kurven füllt die Fläche vollständig aus.
Erläuterung des Konstruktionsverfahrens
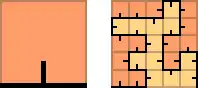
Einem Quadrat wird eine E-Kurve der Stufe einbeschrieben:
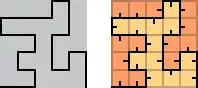
Um leichter darstellen zu können, wie in der Folge die einzelnen Segmente des Linienzuges ersetzt werden, wird das folgende Muster angewendet, bei dem einerseits zwischen hellen und dunklen Teilquadraten unterschieden wird und andererseits jeweils die Orientierung der Quadrate (siehe Markierung) beachtet werden muss:
In der Folge werden die dunklen Quadrate durch dasselbe Muster ersetzt (Orientierung beachten!)
... und die hellen Quadrate durch das negative Abbild des Musters (Orientierung beachten!).
Nach diesem Schritt erhält man eine E-Kurve der Stufe n = 2:
Wendet man diese nochmals an, erhält man eine E-Kurve der Stufe n = 3:
Durch weitere Anwendung dieses Verfahren kann man E-Kurven beliebiger Stufen erhalten.
Die Darstellung der Stufen n = 1, 2, 3 in einem gemeinsamen Bild:
Siehe auch
Weblinks
Einzelnachweise
- Douglas M.McKenna: SquaRecurves, E-Tours, Eddies, and Frenzies: Basic Families of Peano Curves on the Square Grid. In: The Lighter Side of Mathematics: Proceedings of the Eugene Strens Memorial Conference on Recreational Mathematics and its History. 1994, ISBN 978-0-88385-516-4.