Rastermethode
Die Rastermethode[1] (eigentlich: „Der Rost“,[2] polnisch Metoda rusztu (deutsch wörtlich: „Rostmethode“), englisch Grill method, französisch Méthode du gril) war ein durch den polnischen Kryptoanalytiker Marian Rejewski in den frühen 1930er-Jahren ersonnenes kryptanalytisches Verfahren zur Erschließung des Schlüssels der deutschen Rotor-Schlüsselmaschine Enigma.

Hintergrund

Seit 1. Juni 1930, mit Indienststellung der Enigma I, verfügte die deutsche Reichswehr über eine – für die damalige Zeit – herausragend sichere Chiffriermaschine. Im Gegensatz zu ihren Vorläuferinnen, wie beispielsweise die Enigma-D, war sie durch eine geheime Zusatzeinrichtung, das exklusiv militärisch genutzte Steckerbrett (Bild), gestärkt worden. Dieses erlaubte die paarweise Vertauschung aller Buchstaben des lateinischen Alphabets.
Das kryptographische Potenzial des Steckerbretts wurde allerdings nicht voll genutzt. Statt alle dreizehn möglichen und verfügbaren Buchstabenpaare zu nutzen, beschränkte man sich in den ersten Jahren darauf, nur sechs davon durch doppelpolige Steckkabel zu vertauschen.[4] Die restlichen vierzehn (14 = 26 – 2×6) Buchstaben blieben „ungesteckert“ (wurden nicht vertauscht). Die so eingestellte Enigma wurde anschließend benutzt, um den für jeden verschlüsselten Funkspruch individuell zu wählenden Spruchschlüssel zu verschlüsseln. Hierbei unterlief den deutschen Stellen ein weiterer Fehler, indem sie eine Verdopplung des Spruchschlüssels vorschrieben.[5]
Methode
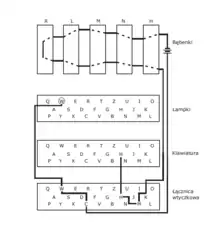

Voraussetzungen zur Durchführung der Rastermethode sind – nachdem das polnische Biuro Szyfrów (deutsch „Chiffrenbüro“) die Funktionsweise der Maschine aufgeklärt und die Verdrahtung der Walzen ermittelt hatte – die oben genannten beiden Verfahrensfehler: Nutzung von nur sechs (der dreizehn möglichen) Steckverbindungen sowie die Spruchschlüsselverdopplung. Die polnischen Kryptoanalytiker konnte ferner davon ausgehen, „dass erstens während des Schlüsselns des Spruchschlüssels eine Drehung der mittleren Walze nur etwa einmal in 5 Fällen auftritt [exakt sind es 5 von 26], und dass zweitens die Steckerverbindung eine Anzahl Buchstaben unverändert lässt.“[6]
Unter diesen Voraussetzungen ist es möglich, eine Relation zwischen dem linken Teil des Walzensatzes, bestehend aus mittlerer und linker Walze sowie der Umkehrwalze (UKW), sowie dem rechten Teil, bestehend aus der sich drehenden rechten Walze, in Form eines Gleichungssystems anzugeben. Da der verdoppelte Spruchschlüssel aus insgesamt sechs Buchstaben besteht, erhält man sechs solche Gleichungen. Die jeweilige linke Seite ist mit Ausnahme eines „Exponenten“, der einen von 26 Werten annehmen kann, für alle sechs Gleichungen konstant. Und die jeweilige rechte Seite gibt die Substitution der rechten Walze an. Rejewski bezeichnete diese Substitution mit dem Buchstaben F. Diese lässt sich für jeden der 26 angenommenen Fälle des Exponenten mithilfe jeder der sechs Gleichungen berechnen. In den meisten Fällen ergeben die sechs Gleichungen unterschiedliche F, mit einer Ausnahme, bei der alle sechs Gleichungen dasselbe F angeben. Das ist die gesuchte Lösung, aus der man die Rotationsposition der rechten Walze ableiten kann.
Die beschriebene Methode hängt davon ab, dass keiner der sechs Buchstaben des verdoppelten Spruchschlüssels und seiner Verschlüsselung „gesteckert“ ist, also durch ein in das Steckerbrett gestecktes Kabel vertauscht wird. Ist das dennoch der Fall, dann gelingt es mit etwas Mühe, die Methode trotzdem anzuwenden, falls nur einige wenige Buchstaben durch „Steckerung“ betroffen sind. Sind allerdings zu viele oder gar alle Buchstaben gesteckert, dann scheitert die Methode. Mit anderen Worten, die Brauchbarkeit der Rastermethode wird durch die Anzahl der Buchstabenvertauschungen beeinträchtigt. Hätten die Deutschen alle dreizehn Buchstabenpaare durch Steckkabel vertauscht, dann hätte die beschriebene Einbruchsmöglichkeit nicht existiert.
In der Praxis ersparten sich die polnischen Kryptoanalytiker die für jeden einzelnen Tagesschlüssel immer wiederkehrenden mühsamen und zeitaufwendigen Untersuchungen und Berechnungen. Sie ersannen stattdessen ein mechanisches Verfahren mithilfe von zwei aufeinanderzulegenden Papierbögen. Auf den unteren schreibt man in 26 untereinanderstehenden Zeilen die durch den linken Teil des Walzensatzes jeweils möglichen Substitutionen. Dabei enthält jede Zeile das jeweils angenommene „verwürfelte“ Substitutionsalphabet. Auf den oberen Bogen schreibt man in sechs Zeilen die durch die sechs Buchstaben des verdoppelten Spruchschlüssels gegebenen Substitutionen, ebenfalls als jeweils 26 verwürfelte Buchstaben. Unterhalb jeder der sechs Zeilen wurden Schlitze geschnitten, durch die man auf das untere Blatt hindurchschauen konnte (Bild).
Das obere Blatt sieht also aus wie ein Gitterrost. Dieser Rost wird auf das untere Blatt gelegt und solange nach oben und unten verschoben, bis man identische Substitutionen auf dem oberen und – durch die Gitterschlitze hindurch – auf dem unteren Blatt entdeckt. Wie gesagt, gilt dies nur, falls man „Glück hat“ und die betroffenen Buchstaben „zufällig“ alle ungesteckert sind. Andernfalls kann es dennoch gelingen, gewisse Symmetrien oder Analogien zwischen Buchstabenpaaren zu erkennen und somit sogar einige Steckerverbindungen zu erschließen. Als Ergebnis erhält man dann einige der gesuchten Stecker sowie die Rotationsposition der rechten Walze.[7]
Nachfolger
Die Rastermethode wurde nach Oktober 1936 nur noch selten verwendet.[8] Stattdessen erstellte man mithilfe eines inzwischen speziell zu diesem Zweck gebauten elektromechanischen kryptanalytischen Hilfsgeräts, genannt das Zyklometer (deutsch wörtlich „Schleifenmesser“), einen sogenannten „Katalog der Charakteristiken“ (polnisch: Katalog charakterystyk). Anhand dessen konnten die gesuchten Schlüssel viel einfacher und schneller ermittelt werden. Die Erzeugung dieses Zyklen-Katalogs, so äußerte sich Rejewski, „war mühsam und dauerte mehr als ein Jahr, aber nachdem er fertig war [... konnten] Tagesschlüssel innerhalb von etwa 15 Minuten [ermittelt werden]“.[9][10]
Literatur
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-67931-6.
- Friedrich L. Bauer: Historische Notizen zur Informatik. Springer, Berlin 2009. ISBN 3-540-85789-3.
- David Kahn: Seizing the Enigma – The Race to Break the German U-Boat Codes, 1939–1943. Naval Institute Press, Annapolis, MD, USA, 2012, ISBN 978-1-59114-807-4.
- Władysław Kozaczuk: Geheimoperation Wicher. Bernard u. Graefe, Koblenz 1989, Karl Müller, Erlangen 1999. ISBN 3-7637-5868-2, ISBN 3-86070-803-1
- Władysław Kozaczuk: Im Banne der Enigma. Militärverlag der Deutschen Demokratischen Republik, 1987, ISBN 3-327-00423-4
- Władysław Kozaczuk & Jerzy Straszak: Enigma – How the Poles Broke the Nazi Code. Hyppocrene Books, New York 2004. ISBN 0-7818-0941-X
- Tadeusz Lisicki: Die Leistung des polnischen Entzifferungsdienstes bei der Lösung des Verfahrens der deutschen »Enigma«-Funkschlüsselmaschine in J. Rohwer und E. Jäkel: Die Funkaufklärung und ihre Rolle im Zweiten Weltkrieg, Motorbuch Verlag, Stuttgart, 1979, S. 66–81. PDF; 1,7 MB. Abgerufen am 11. März 2019.
- Marian Rejewski und Henryk Zygalski: Kurzgefasste Darstellung der Auflösungsmethoden. Bertrand Archiv SHD DE 2016 ZB 25/6, Dossiers Nos. 281 und 282, ca. 1940.
- Dermot Turing: X, Y & Z – The Real Story of how Enigma was Broken. The History Press, 2018, ISBN 978-0-75098782-0.
Weblinks
- Geheimoperation Wicher Beschreibung des polnischen Beitrags zum Bruch der Enigma.
Einzelnachweise
- Friedrich L. Bauer: Historische Notizen zur Informatik. Springer, Berlin 2009, S. 301. ISBN 3-540-85789-3.
- Marian Rejewski und Henryk Zygalski: Kurzgefasste Darstellung der Auflösungsmethoden. Bertrand Archiv SHD DE 2016 ZB 25/6, Dossiers Nos. 281 und 282, ca. 1940, S. 24–26.
- Craig P. Bauer: Secret History|– The Story of Cryptology. CRC Press, Boca Raton 2013, S. 248. ISBN 978-1-4665-6186-1.
- Louis Kruh, Cipher Deavours: The Commercial Enigma – Beginnings of Machine Cryptography. Cryptologia, Vol. XXVI, Nr. 1, Januar 2002, S. 11. apprendre-en-ligne.net (PDF; 0,8 MB), abgerufen am 11. März 2019.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 412.
- Marian Rejewski und Henryk Zygalski: Kurzgefasste Darstellung der Auflösungsmethoden. Bertrand Archiv SHD DE 2016 ZB 25/6, Dossiers Nos. 281 und 282, ca. 1940, S. 24.
- Marian Rejewski und Henryk Zygalski: Kurzgefasste Darstellung der Auflösungsmethoden. Bertrand Archiv SHD DE 2016 ZB 25/6, Dossiers Nos. 281 und 282, ca. 1940, S. 26.
- Friedrich L. Bauer: Historische Notizen zur Informatik. Springer, Berlin 2009, S. 301–302. ISBN 3-540-85789-3.
- Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. 3., überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2000, S. 417.
- Dermot Turing: X, Y & Z – The Real Story of how Enigma was Broken. The History Press, Stroud 2018, ISBN 978-0-75098782-0, S. 67.