Quadratrix des Hippias

Die Quadratrix oder Trisektrix des Hippias (auch Quadratrix des Dinostratos) ist eine kinematisch erzeugte Kurve, deren Erfindung der Überlieferung nach dem griechischen Sophisten Hippias von Elis (5. Jahrhundert v. Chr.) zugeschrieben wird. Sie ist eines der ältesten Beispiele einer kinematisch erzeugten Kurve und wurde benutzt, um zwei der drei großen antiken geometrischen Probleme, die Dreiteilung des Winkels und die Quadratur des Kreises, zu lösen. Hippias verwendete sie um 420 v. Chr. zur Dreiteilung des Winkels (daher Trisektrix) und Dinostratos um 350 v. Chr. zur Quadratur des Kreises (daher Quadratrix).

Quadratrix (rot); Momentaufnahme für F und E bei sechs Zehnteln ihres Weges

Definition

Quadratrix als ebene Kurve (a=1)

Quadratrix als Funktion (a=1)

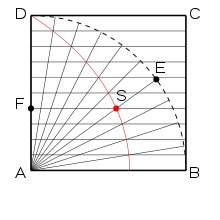
Im Quadrat ABCD sei ein Viertelkreis um A mit der Seitenlänge des Quadrates als Radius eingezeichnet. Ein Punkt E durchlaufe den Viertelkreis von D nach B mit konstanter Winkelgeschwindigkeit. Ebenfalls mit konstanter Geschwindigkeit durchlaufe F die Strecke DA, und zwar so, dass E und F gleichzeitig in D loslaufen und gleichzeitig in B bzw. A ankommen. Die Quadratrix ergibt sich dann als Ortskurve des Schnittpunkts S der Strecke AE mit der Parallelen zu AB durch F.[1][2]

Platziert man das obige Quadrat mit einer gegebenen Seitenlänge a so in einem (kartesischen) Koordinatensystem, dass die Seite AB auf der x-Achse und der Punkt A im Ursprung liegt, dann wird die Quadratrix durch eine ebene Kurve ${\displaystyle \gamma$ beschrieben und es gilt:

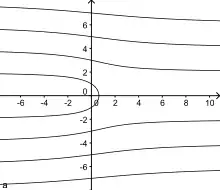
\gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}{\frac {2a}{\pi }}t\cot(t)\\{\frac {2a}{\pi }}t\end{pmatrix}}

Diese Darstellung kann man nun auch verwenden, um die Quadratrix außerhalb ihres zugehörigen Quadrates zu definieren, wobei sie allerdings an den Definitionslücken des $\cot(t)$ nicht definiert ist. Sie ist aber an der formalen Definitionslücke bei $t=0$ wegen $\lim _{t\to 0}t\cot(t)=1$ stetig fortsetzbar. Dadurch erhält man eine stetige Kurve auf dem Intervall $(-\pi ,\pi )$ .[3][4]

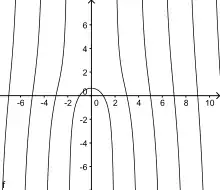
Möchte man die Quadratrix als (einfach darstellbare) Funktion beschreiben, so ist es zweckmäßig, die x- und y-Achsen zu vertauschen, das heißt, man legt AB auf die y-Achse anstatt auf die x-Achse. Dann wird die Quadratrix durch die folgende Funktion f(x) beschrieben:[5][6]

f(x)=x\cdot \cot \left({\frac {\pi }{2a}}\cdot x\right)

Winkelteilung

Quadratrix-Zirkel

Dreiteilung eines Winkels

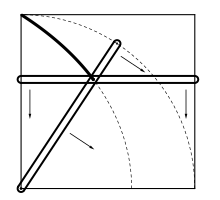
Die Dreiteilung eines beliebigen Winkels ist mit Zirkel und Lineal nicht möglich. Erlaubt man jedoch die Verwendung einer Quadratrix als ein weiteres Hilfsmittel, das heißt setzt man voraus, dass über einem Winkelschenkel eine Quadratrix gezeichnet werden kann, dann ist es möglich, einen beliebigen Winkel in n gleich große Winkel zu unterteilen. Damit ist dann insbesondere auch die Dreiteilung eines Winkels möglich (n = 3). Zu einem Quadrat mit fest vorgegebener Länge kann man eine Quadratrix zum Beispiel mit Hilfe eines Quadratrix-Zirkels oder einer Quadratrix-Schablone zeichnen.[1][2]

Da nach Definition der Quadratrix der durchlaufene Winkel proportional zum durchlaufenen Streckenabschnitt auf der Quadratseite ist, liefert eine Einteilung dieses Streckenabschnitts in n gleich große Teile auch eine Einteilung des zugehörigen Winkels in n gleich große Teile. Die Einteilung einer beliebigen Strecke in n Teile ist aufgrund des Strahlensatzes mit Zirkel und Lineal möglich.

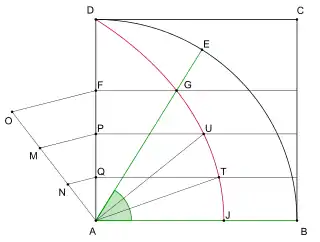
Zu einem gegebenen Winkel BAE (≤ 90°) errichtet man zunächst über seinem Schenkel AB ein Quadrat ABCD und zeichnet die zugehörige Quadratrix. Der zweite Schenkel des Winkels schneidet die Quadratrix in einem Punkt G, und die zum Schenkel AB parallele Gerade durch G schneidet die Quadratseite AD in F; dann ist AF der zum Winkel BAE proportionale Streckenabschnitt. Nun trägt man auf einem von A ausgehenden Strahl n äquidistante Punkte ab und verbindet den letzten Punkt O mit F. Man zeichnet die zu OF parallelen Geraden durch die äquidistanten Punkte; deren Schnittpunkte mit der Strecke AF liefern dann die Einteilung dieser Strecke in n gleich große Teile. Die Parallelen zur Quadratseite AB durch diese Schnittpunkte schneiden die Quadratrix. Die Schnittpunkte auf der Quadratrix teilen dann den Winkel BAE in n gleich große Teile.[5]

Mit Zirkel und Lineal alleine kann man nicht jeden Punkt der Quadratrix erzeugen, sondern nur eine dichte Teilmenge. Damit kann man eine Quadratrix zwar beliebig gut annähern, aber eine exakte Winkelteilung ohne ein Gerät zur Erzeugung einer Quadratrix ist im allgemeinen Fall nicht möglich, da die benötigten Quadratrixpunkte nicht in dieser mit Hilfe von Zirkel und Lineal konstruierbaren Teilmenge liegen müssen.[2][3]

Quadratur des Kreises

Quadratur des Viertelkreises mit r=1

Die Quadratur des Kreises mit Zirkel und Lineal alleine ist unmöglich. Lässt man jedoch als weiteres Hilfsmittel die Quadratrix des Hippias zu, dann ermöglicht der Satz des Dinostratos, mit Zirkel und Lineal ein zu einem Viertelkreis flächengleiches Quadrat zu konstruieren. Das Quadrat mit doppelter Seitenlänge hat dann den gleichen Flächeninhalt wie der volle Kreis.

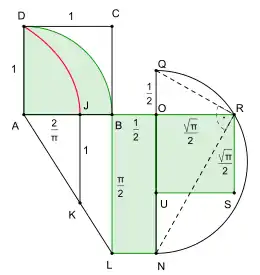
Der Satz des Dinostratos besagt, dass die Quadratrix des Hippias die Seite des zugehörigen Quadrates im Verhältnis ${\tfrac {2}{\pi }}$ teilt.[1] Zu einem gegebenen Viertelkreis mit Radius r konstruiert man zunächst das zugehörige umschriebene Quadrat ABCD mit Seitenlänge r. Dann schneidet die Quadratrix dieses Quadrates die Quadratseite AB in J und es gilt $\left|{\overline {AJ}}\right|={\tfrac {2}{\pi }}r$ . Nun errichtet man in J eine Strecke JK, die senkrecht zu AB ist und die Länge r hat. Dann schneidet die Gerade AK die verlängerte Seite BC in L. Nach dem Strahlensatz gilt $\left|{\overline {BL}}\right|={\tfrac {\pi }{2}}r$ . Wenn man die Quadratseite AB über B hinaus um die Strecke $\left|{\overline {BO}}\right|={\tfrac {r}{2}}$ verlängert, dann bilden BL und BO die Grundseite eines Rechtecks OBLN, dessen Fläche der des Viertelkreises entspricht. Zu diesem Rechteck lässt sich mit Hilfe des Höhensatzes von Euklid und des Satzes des Thales ein flächengleiches Quadrat konstruieren (siehe auch Quadratur des Rechtecks). Dazu verlängert man die Rechteckseite ON um die Strecke $\left|{\overline {OQ}}\right|={\tfrac {r}{2}}$ , errichtet einen Halbkreis mit NQ als Durchmesser und verlängert die Strecke AO so, dass sie den Halbkreis in R schneidet. Nach dem Satz des Thales ist das Dreieck NQR rechtwinklig, und nach dem Höhensatz des Euklid ist seine Höhe OR die Grundseite eines Quadrates, das flächengleich zum Rechteck OBLN und damit auch zum Viertelkreis ist.[7]

Der Schnittpunkt J der Quadratrix mit der Quadratseite AB ist jedoch bei Anwendung der geometrischen Definition nicht definiert, da an dieser Stelle die beiden zu schneidenden Strecken zusammenfallen und kein eindeutiger Schnittpunkt existiert. Damit lässt sich der Punkt J weder mit Zirkel und Lineal noch mit Hilfe des obigen Quadratrix-Zirkels "exakt" konstruieren.[8][9]

Historisches

In historischen Quellen wird die Quadratrix bei Proklos (412–485), Pappos (3./4. Jahrhundert) und Iamblichos (ca. 240–325) erwähnt. Proklos gibt Hippias als den Entdecker einer als Quadratrix bezeichneten Kurve an und beschreibt an einer anderen Stelle, wie Hippias diese Kurve zur Dreiteilung eines beliebigen Winkels verwendet. Pappos hingegen beschreibt, wie eine als Quadratrix bezeichnete Kurve von Dinostratos, Nikomedes und anderen zur Quadratur des Kreises verwendet wurde. Dabei erwähnt er jedoch weder Hippias namentlich, noch benennt er explizit einen Entdecker der Kurve. Iamblichos gibt lediglich in einem kurzen Satz an, dass Nikomedes eine als Quadratrix bezeichnete Kurve zur Quadratur des Kreises verwendet hat.[10][11][12]

Obwohl es aufgrund der Bezeichnung der Kurve als Quadratrix bei Proklos denkbar ist, dass Hippias die Kurve auch selbst zur Quadratur verwendet hat, wird diese Quellenlage von Mathematikhistorikern meist so gedeutet, dass Hippias die Kurve zwar entdeckt, aber selbst nur zur Dreiteilung des Winkels verwandt hat und ihre Anwendung zur Quadratur auf spätere Mathematiker, insbesondere Dinostratos und Nikomedes zurückgeht. Diese Lesart der historischen Quellen geht auf Moritz Cantor zurück.[11][12]

Literatur

Hans-Wolfgang Henn: Elementare Geometrie und Algebra. Verlag Vieweg+Teubner, 2003, S. 45–48 Die Quadratur des Kreises (Auszug (Google))
Felix Klein: Famous Problems of Elementary Geometry. Cosimo 2007 (Nachdruck), ISBN 978-1-60206-417-1, S. 57–58 (Auszug (Google))
Audun Holme: Geometry: Our Cultural Heritage. Springer 2010, ISBN 978-3-642-14440-0, S. 114–116 (Auszug (Google))
Thomas Little Heath: A History of Greek Mathematics. Volume 1. From Thales to Euclid. Clarendon Press 1921 (Nachdruck Elibron Classics 2006), S. 225–230 (archive.org)
Horst Hischer: Klassische Probleme der Antike – Beispiele zur „Historischen Verankerung“. (PDF; 539 kB). In: Jürgen Blankenagel, Wolfgang Spiegel (Hrsg.): Mathematikdidaktik aus Begeisterung für die Mathematik – Festschrift für Harald Scheid. Klett, Stuttgart/Düsseldorf/Leipzig 2000, S. 97–118.
Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA 2010, ISBN 978-0-88385-348-1, S. 146–147 (Auszug (Google))

Weblinks

Commons: Quadratrix of Hippias – Sammlung von Bildern, Videos und Audiodateien

Quadratrix und die Quadratur des Kreises. Universität Lüneburg
Michael D. Huberty, Ko Hayashi, Chia Vang: Hippias’ Quadratrix
Eric W. Weisstein: Quadratrix of Hippias. In: MathWorld (englisch).
John J. O’Connor, Edmund F. Robertson: Quadratrix of Hippias. In: MacTutor History of Mathematics archive.
Suzanne Harper, Shannon Driskell: An Investigation of Historical Geometric Constructions. In: Convergence, August 2010

Einzelnachweise

Horst Hischer: Klassische Probleme der Antike – Beispiele zur „Historischen Verankerung“ (PDF; 539 kB). In: Jürgen Blankenagel, Wolfgang Spiegel (Hrsg.): Mathematikdidaktik aus Begeisterung für die Mathematik – Festschrift für Harald Scheid. Klett, Stuttgart/Düsseldorf/Leipzig 2000, S. 97–118.
Hans-Wolfgang Henn: Elementare Geometrie und Algebra. Verlag Vieweg+Teubner 2003, S. 45–48 Die Quadratur des Kreises (Auszug (Google))
Hans Niels Jahnke: A History of Analysis. American Mathematical Society 2003, ISBN 0-8218-2623-9, S. 30–31 (Auszug (Google))
Eric W. Weisstein: Quadratrix of Hippias. In: MathWorld (englisch).
Dudley Underwood: The Trisectors. Cambridge University Press 1994, ISBN 0-88385-514-3, S. 6–8 (Auszug (Google))
John J. O’Connor, Edmund F. Robertson: Quadratrix of Hippias. In: MacTutor History of Mathematics archive.
Audun Holme: Geometry: Our Cultural Heritage. Springer 2010, ISBN 978-3-642-14440-0, S. 114–116 (Auszug (Google))
Jean-Paul Delahaye: Pi – Die Story. Springer 1999, ISBN 3-7643-6056-9, S. 71 (Auszug (Google))
John J. O’Connor, Edmund F. Robertson: Dinostratus. In: MacTutor History of Mathematics archive.
Van der Waerden: Science Awakening. Oxford University Press 1961, S. 146
James Gow: A Short History of Greek Mathematics. 1884, Reprint: Cambridge University Press 2010, ISBN 978-1-108-00903-4, S. 162–164 (Auszug (Google))
Thomas Little Heath: A History of Greek Mathematics. Volume 1. From Thales to Euclid. Clarendon Press 1921 (Nachdruck Elibron Classics 2006), S. 182, 225–230 (archive.org).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Hischer-1] Horst Hischer: Klassische Probleme der Antike – Beispiele zur „Historischen Verankerung“ (PDF; 539 kB). In: Jürgen Blankenagel, Wolfgang Spiegel (Hrsg.): Mathematikdidaktik aus Begeisterung für die Mathematik – Festschrift für Harald Scheid. Klett, Stuttgart/Düsseldorf/Leipzig 2000, S. 97–118.

[Henn-2] Hans-Wolfgang Henn: Elementare Geometrie und Algebra. Verlag Vieweg+Teubner 2003, S. 45–48 Die Quadratur des Kreises (Auszug (Google))

[Jahnke-3] Hans Niels Jahnke: A History of Analysis. American Mathematical Society 2003, ISBN 0-8218-2623-9, S. 30–31 (Auszug (Google))

[MathWorld-4] Eric W. Weisstein: Quadratrix of Hippias. In: MathWorld (englisch).

[Underwood-5] Dudley Underwood: The Trisectors. Cambridge University Press 1994, ISBN 0-88385-514-3, S. 6–8 (Auszug (Google))

[MactTutor1-6] John J. O’Connor, Edmund F. Robertson: Quadratrix of Hippias. In: MacTutor History of Mathematics archive.

[Holme-7] Audun Holme: Geometry: Our Cultural Heritage. Springer 2010, ISBN 978-3-642-14440-0, S. 114–116 (Auszug (Google))

[Delahaye-8] Jean-Paul Delahaye: Pi – Die Story. Springer 1999, ISBN 3-7643-6056-9, S. 71 (Auszug (Google))

[MactTutor2-9] John J. O’Connor, Edmund F. Robertson: Dinostratus. In: MacTutor History of Mathematics archive.

[Van_der_Waerden-10] Van der Waerden: Science Awakening. Oxford University Press 1961, S. 146

[Gow-11] James Gow: A Short History of Greek Mathematics. 1884, Reprint: Cambridge University Press 2010, ISBN 978-1-108-00903-4, S. 162–164 (Auszug (Google))

[Heath-12] Thomas Little Heath: A History of Greek Mathematics. Volume 1. From Thales to Euclid. Clarendon Press 1921 (Nachdruck Elibron Classics 2006), S. 182, 225–230 (archive.org).