Quadratur des Rechtecks

Die Quadratur des Rechtecks ist eine klassische Aufgabe der Geometrie. Mit Lineal und Zirkel soll aus einem gegebenen Rechteck ein Quadrat mit gleich großer Fläche gezeichnet werden. Im Gegensatz zur Quadratur des Kreises, die unlösbar ist, ist die Quadratur des Rechtecks auf verschiedene Arten möglich.

Ausgangslage

Rechtwinkliges Dreieck

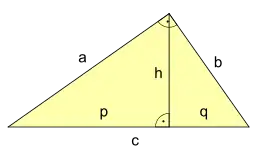
Ausgangspunkt für die folgenden beiden Konstruktionen sind zwei auf Euklid zurückgehende mathematische Gesetze des rechtwinkligen Dreiecks, der Höhensatz und der Kathetensatz.

In einem rechtwinkligen Dreieck seien a und b die den rechten Winkel einschließenden Katheten und c die Hypotenuse. h sei die Höhe auf die Seite c, und p bzw. q seien die beiden Hypotenusenabschnitte. Dann gelten folgende Beziehungen:

$h^{2}=p\cdot q$ (Höhensatz von Euklid)

$a^{2}=c\cdot p$ und $b^{2}=c\cdot q$ (Kathetensatz von Euklid)

Methode mit dem Höhensatz

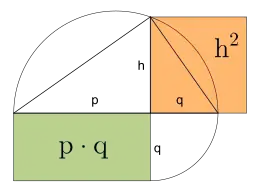
Quadratur mit Hilfe des Höhensatzes

Ganz egal, welche Proportionen das gegebene (hier grüne) Rechteck hat: Wir nehmen an, seine eine Seite wäre der Hypotenusenabschnitt p und seine andere Seite der Hypotenusenabschnitt q eines rechtwinkligen Dreiecks. Dann schwenken wir die (hier) kürzere Seite des Rechtecks um 90° und erhalten die Basis eines rechtwinkligen Dreiecks. Über dieser Basis zeichnen wir einen Thaleskreis. Die Verlängerung der kürzeren Rechteckseite schneidet den Thaleskreis und liefert die Höhe des rechtwinkligen Dreiecks mit den Hypotenusenabschnitten p und q. Wenn man nun über dieser Höhe ein (hier oranges) Quadrat errichtet, hat dieses exakt denselben Flächeninhalt wie das gegebene Rechteck.

Methode mit dem Kathetensatz

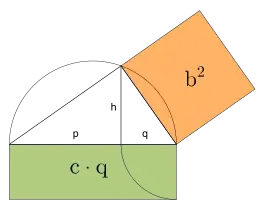
Quadratur mit Hilfe des Kathetensatzes

Bei der zweiten Methode nimmt man an, die längere Seite des (hier grünen) Rechtecks würde sich über die gesamte Basis c eines rechtwinkligen Dreiecks erstrecken. Dann dreht man die kürzere Seite des Rechtecks um 90° nach innen, sie liefert den Hypotenusenabschnitt q und den Fußpunkt der Höhe h. Dann zeichnet man über der Basis c einen Thaleskreis. Der Schnittpunkt der Höhe mit der Kreislinie ergibt den dritten Dreieckspunkt, wodurch sich die Kathete b ergibt. Wenn man nun über b ein (hier oranges) Quadrat errichtet, hat dieses exakt denselben Flächeninhalt wie das gegebene Rechteck.

Methode mit dem Sekanten-Tangenten-Satz

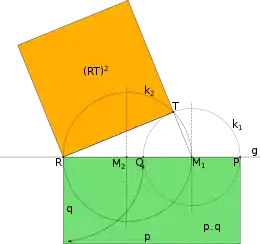
Quadratur mit Hilfe des Sekanten-Tangenten-Satzes

Auch der Sekanten-Tangenten-Satz lässt sich für die Quadratur des Rechtecks verwenden: In einem gegebenen (hier grünen) Rechteck mit Länge p und Breite q, sei eine Länge p auch als Strecke PR gekennzeichnet. Sei die Strecke QR gleich der Breite q und innerhalb PR. Sei M₁ der Mittelpunkt der Strecke PQ. Sei k₁ der Kreis mit Durchmesser PQ, und k₂ der Kreis mit Durchmesser M₁R. Sei T ein Schnittpunkt dieser Kreise. Der Winkel M₁TR ist nach dem Satz von Thales ein rechter, daher ist RT eine Tangente an k₁. Nach dem Sekanten-Tangenten-Satz gilt nun (RT)² = p·q.

Methode mit dem Sehnensatz

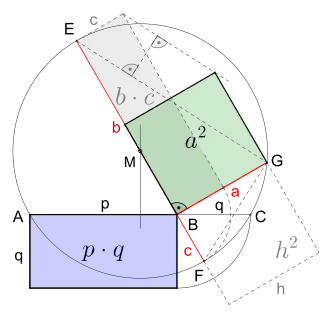
Quadratur mit Hilfe des Sehnensatzes
Das graue Rechteck b · c und die gestrichelten Linien sind für die Lösung nicht erforderlich, sie sollen lediglich die Lösung verdeutlichen, z. B. aus welchem Grund die Strecke BG eine Seite a des flächengleichen Quadrates ist.

Zu den vier bekanntesten Lösungen zur Flächenumwandlung zählt auch die, die mit Hilfe des Sehnensatzes darstellbar ist.[1]
Für die Quadratur eines gegebenen (hier blauen) Rechtecks mit Länge p und Breite q, werden zuerst zwei Ecken einer langen Seite mit A bzw. B bezeichnet. Es folgt die Verlängerung der Strecke AB um die Breite q mit Hilfe des Viertelkreises, dabei ergibt sich die Strecke AC. Nach dem Einzeichnen der Mittelsenkrechten von AC wird auf der Mittelsenkrechten der frei wählbare Punkt M bestimmt. Nun zeichnet man einen Kreis um den Punkt M mit dem Radius |MA|; hiermit wird die Strecke AC zur ersten Sehne des Kreises. Es geht weiter, indem der Durchmesser des Kreises durch den Punkt B gezogen wird. Die damit entstandene Strecke EF ist die zweite Sehne des Kreises. Beide Sehnen kreuzen sich im Punkt B, der seinerseits die Sehne AC in p und q sowie die Sehne EF in b und c unterteilt. Schließlich wird eine Senkrechte auf die Strecke EB errichtet, die ab dem Punkt B bis auf die Kreislinie verläuft und den Schnittpunkt G erzeugt. Somit ergibt sich als Strecke BG die erste Seite a des gesuchten flächengleichen (hier grünen) Quadrates.

Wie beschrieben ist in der nebenstehenden Zeichnung die Sehne EF durch den Mittelpunkt des Kreises gezogen. Auf Grund dessen besteht bezüglich Verdeutlichung und Begründung des Ergebnisses die Möglichkeit (wie dargestellt), zusätzlich zur Rechteckfläche b · c für die Umwandlung in die Quadratfläche a²,[2] auch das rechtwinklige Dreieck EFG mit der Höhe h = a und die Quadratfläche h² einzuzeichnen. Alles zusammen gesehen, ist der Zusammenhang des Sehnensatzes mit dem Höhensatz deutlich erkennbar.

Gemäß dem Sehnensatz gilt:

{\overline {AB}}\cdot {\overline {BC}}={\overline {EB}}\cdot {\overline {BF}}

bzw.

p\cdot q=b\cdot c,

daraus folgt (wie im Höhensatz von Euklid)

a^{2}=p\cdot q,

zieht man daraus die Quadratwurzel, ist die Seitenlänge a des Quadrates gleich dem geometrischen Mittel der Länge p + q.[3]

a={\sqrt {pq}}

Zerlegung in Quadrate

Analog zur Quadratur des Quadrates kann man auch das Problem betrachten, ein Rechteck in Quadrate verschiedener Größe zu zerlegen (Quadratur des Rechtecks). Die erste Lösung fand 1925 der polnische Mathematiker Zbigniew Morón (1904–1971). Er zerlegte ein 33 × 32 Rechteck in 9 Quadrate mit Seitenlängen 1,4,7,8,9,10, 14, 15, 18 und ein 65 × 47 Rechteck in 10 Quadrate mit Seitenlängen 3,5,6,11, 17, 19, 22, 23, 24, 25.[4] 1939 folgte die erste Quadratur eines Quadrats durch Roland Sprague und 1940 durch William Thomas Tutte und Kollegen.

Siehe auch

Literatur

Schülerduden – Mathematik I. Bibliographisches Institut & F.A. Brockhaus, Mannheim 2008, ISBN 978-3-411-04208-1, S. 193, 212, 415–417
Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik: 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen. Springer, 2015, ISBN 978-3-662-45461-9, S. 31–32

Weblinks

Commons: Rectangle squaring – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Rectangle Squaring. In: MathWorld (englisch).
Euklid’s Elemente Zweytes Buch, Der 14. Satz. – Quadratur des Rechtecks in den Elementen des Euklid
Vom Rechteck, das ein Quadrat werden wollte (PDF)
Quadratur des Rechtecks auf mathematische-basteleien.de

Einzelnachweise

Emese Vargyas, Ysette Weiss-Pidstrygach: 5 Geschichte der Mathematik im Unterricht am Beispiel des Sehnensatzes S. 279–283, siehe S. 281, Abb. 4. (PDF) In: Um welche Flächen geht es beim Sehnensatz? mathematica-didactica.com, 2015, abgerufen am 28. April 2019.
John M. Lee: Axiomatic Geometry. Hrsg.: American Mathematical Society. Rhode Island 2013, S. 303 ff. (Construction Problem 16.20 (Rectangle with a Given Area and Edge) [abgerufen am 5. Mai 2017]).
Universität Magdeburg A.14 Mittelwerte. Mittlere Proportionale, Seite 2, Punkt u. Bild: b) (PDF) abgerufen am 7. Mai 2017
Clifford Pickover: The Math Book. Sterling Publ. 2012, S. 352

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Emese Vargyas, Ysette Weiss-Pidstrygach: 5 Geschichte der Mathematik im Unterricht am Beispiel des Sehnensatzes S. 279–283, siehe S. 281, Abb. 4. (PDF) In: Um welche Flächen geht es beim Sehnensatz? mathematica-didactica.com, 2015, abgerufen am 28. April 2019.

[2] John M. Lee: Axiomatic Geometry. Hrsg.: American Mathematical Society. Rhode Island 2013, S. 303 ff. (Construction Problem 16.20 (Rectangle with a Given Area and Edge) [abgerufen am 5. Mai 2017]).

[Magdeburg-3] Universität Magdeburg A.14 Mittelwerte. Mittlere Proportionale, Seite 2, Punkt u. Bild: b) (PDF) abgerufen am 7. Mai 2017

[4] Clifford Pickover: The Math Book. Sterling Publ. 2012, S. 352