Perfekt bayessches Gleichgewicht

Das perfekt bayessche Gleichgewicht (kurz: PBG) ist ein Lösungskonzept in der Spieltheorie. Es dient dem Lösen von dynamischen Spielen mit unvollständiger Information.

Da bei unvollständiger Information unglaubwürdige Nash-Gleichgewichte nicht mehr durch Teilspielperfektheit ausgeschlossen werden können, wird das Gleichgewichtskonzept um die Komponente der sequentiellen Rationalität und durch sogenannte „Beliefs“ (Einschätzungen bzw. Vermutungen über die Eintrittswahrscheinlichkeit) erweitert. Dieser Ansatz wurde erstmals 1991 bei Drew Fudenberg und Jean Tirole erwähnt.[1]

Nicht zu verwechseln ist das perfekt bayessche Gleichgewicht mit dem bayesschen Gleichgewicht, da Letzteres für statische Spiele vorgesehen ist.

Unvollständige und imperfekte Information

Spiele mit unvollständiger Information lassen sich nicht oder nur in Spezialfällen analysieren. Deshalb werden sie als Spiele mit vollständiger, aber imperfekter (unvollkommener) Information modelliert (Harsanyi-Transformation). Imperfekte Information bedeutet, dass mindestens ein Spieler nicht die komplette Historie des Spiels kennt.[1] Bei einem Spiel in Extensivform zeigt sich dies, wenn mindestens ein Spieler eine Informationsmenge mit mehr als einem Entscheidungsknoten hat. Perfekte Information gibt es also nur, wenn alle Informationsmengen im Spiel einelementig sind.

Während Schach ein Beispiel für Spiele mit vollständiger Information ist (sofern vollständige Erinnerung angenommen wird), ist Poker ein Beispiel für ein Spiel mit imperfekter Information. Hier werden die Karten zufällig verteilt. So kennt ein Spieler zwar seine eigenen Karten, aber nicht die seiner Mitspieler und umgekehrt. Nur deshalb kann Bluffen sinnvoll sein.

Spiele mit imperfekter Information werden mit einem Zufallszug am Beginn des Spieles modelliert. Dieser Zufallszug entscheidet über die Typen oder Eigenschaften der Spieler (bei Poker über die Karten der Spieler). In der Literatur findet man auch oft die Bezeichnung „Naturzug“, da die Natur quasi als zusätzlicher Spieler eingefügt wird. Geht man von vollständiger Information aus, ist jedem Spieler die Wahrscheinlichkeitsverteilung eines Zufallszugs bekannt und damit der gesamte Spielbaum inklusive der Auszahlungen (Common Knowledge).

Bei unvollständiger Information sind die Bedingungen, unter denen das Spiel gespielt wird, hingegen nicht jedem bekannt. So kann es zum Beispiel sein, dass ein Spieler nicht die Auszahlungen bzw. Präferenzen der anderen Spieler kennt, wohl aber seine eigenen. Folglich könnte dieser Spieler auch keinerlei Vermutung über deren Strategien aufstellen. Unter diesen Umständen kann kein glaubwürdiges Gleichgewicht gebildet werden.[2]

Definition perfekt bayessches Gleichgewicht

Mit dem perfekt bayesschen Gleichgewicht lassen sich unglaubwürdige Gleichgewichte ausschließen, sofern bestimmte Kriterien erfüllt sind. Es besteht aus einem Profil von Strategien und einem System von Einschätzungen ${\begin{aligned}(\sigma ,\mu )\end{aligned}}$ , die den Forderungen eins bis vier genügen:

Forderung 1:

Jeder Spieler muss an jeder seiner Informationsmengen Wahrscheinlichkeitseinschätzungen (engl. Beliefs) darüber haben, an welchem Knoten er sich befindet.

Forderung 2:

Gegeben diese Einschätzungen verhalten sich die Spieler sequentiell rational. Das erfordert optimale Reaktionen jeden Spielers an jeder Informationsmenge, gegeben, dass die Informationsmenge erreicht wird und gegeben der Strategien der anderen Spieler ab diesem Zug.

Forderung 3:

In allen Informationsmengen auf dem Gleichgewichtspfad werden die Einschätzungen entsprechend dem Satz von Bayes gebildet. Eine Informationsmenge ist auf dem Gleichgewichtspfad, wenn einer ihrer Knoten mit positiver Wahrscheinlichkeit erreicht wird, gegeben der Gleichgewichtsstrategien der Spieler.

Forderung 4:

In Informationsmengen außerhalb des Gleichgewichtspfades („off-equilibrium“) werden die Einschätzungen mit der bayesschen Regel gebildet, wann immer möglich (s. u.). Ist dies nicht möglich, können die Einschätzungen frei gewählt werden.

Einige Autoren begnügen sich mit den Forderungen 1 bis 3, um ein perfekt bayessches Gleichgewicht zu definieren. Dies wird oftmals auch als schwaches perfekt bayessches Gleichgewicht bezeichnet. Dennoch ist Forderung 4 notwendig um unplausible Gleichgewichte auszuschließen.[3]

Beispiel I

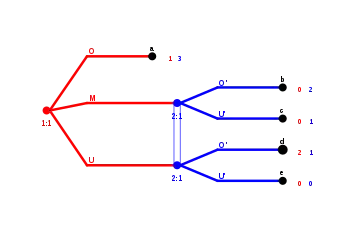
Spiel 1; Dieses Spiel hat keine echten Teilspiele. Es geht auf den deutschen Volkswirt und Mathematiker Reinhard Selten zurück.

Spiel 1 zeigt warum eine Verfeinerung des Gleichgewichtskonzepts notwendig ist, um in dynamischen Spielen mit imperfekter Information unglaubwürdige Nash-Gleichgewichte auszuschließen. Dargestellt ist das Spiel in Extensivform, um die zeitliche Abfolge der Entscheidungen zu verdeutlichen. Die möglichen Auszahlungen sind an den Endknoten (a,b,c,d,e) gegeben. Spiel 1 hat keine echten Teilspiele. Ein Teilspiel beginnt an einer einelementigen Informationsmenge und beinhaltet alle nachfolgenden Entscheidungsknoten, sofern deren Informationsmengen komplett enthalten sind. Folglich ist jedes Nash-Gleichgewicht im gesamten Spiel trivialerweise auch teilspielperfekt.

Zuerst kann Spieler 1 (Rot) zwischen den reinen Strategien O, M und U wählen. Spieler 2 (Blau) entscheidet sich anschließend zwischen den reinen Strategien O' und U'. Spielt Spieler 1 O, so endet das Spiel mit der Auszahlung (1,3). Dies bedeutet, dass Spieler 1 die Auszahlung 1 und Spieler 2 die Auszahlung 3 bekommt. Wählt Spieler 1 M oder U, so wird die Informationsmenge von Spieler 2 erreicht. Dieser lernt nun, dass entweder M oder U gespielt wurde.

In der Normalform des Spieles lässt sich erkennen, dass es genau zwei Nash-Gleichgewichte in reinen Strategien gibt. Diese sind ${\begin{aligned}(O,U')\end{aligned}}$ und ${\begin{aligned}(U,O')\end{aligned}}$ , mit den Auszahlungen (1,3) beziehungsweise (2,1).

Spieler 1/Spieler 2	O'	U'
O	(1, 3)	(1, 3)
M	(0, 2)	(0, 1)
U	(2, 1)	(0, 0)

Da U' dominiert ist, wird Spieler 2 niemals U' spielen, gegeben, dass die Informationsmenge erreicht wird. Das Gleichgewicht ${\begin{aligned}(O,U')\end{aligned}}$ ist daher unglaubwürdig. Unglaubwürdige Gleichgewichte können nun mit dem Konzept des perfekt bayesschen Gleichgewicht ausgeschlossen werden.

Dazu muss Spieler 2 zunächst an seiner Informationsmenge Einschätzungen darüber bilden, an welchem Knoten er sich befindet: Die Wahrscheinlichkeit, an Knoten 1 (oben) zu sein, sei nun $p$ . Diejenige an Knoten 2 zu sein, sei $(1-p)$ .

Spielt Spieler 2 O', ist seine erwartete Auszahlung also ${\begin{aligned}p*2+(1-p)*1=p+1\end{aligned}}$ . Die erwartete Auszahlung der Strategie U' ist hingegen ${\begin{aligned}p*1+(1-p)*0=p\end{aligned}}$ . Da ${\begin{aligned}p+1>p\end{aligned}}$ , ist O' für Spieler 2 strikt dominant. Das Gleichgewicht ${\begin{aligned}(O,U')\end{aligned}}$ ist deswegen nicht kompatibel mit den ersten beiden Forderungen und folglich kein perfekt bayessches Gleichgewicht.

Im Allgemeinen wird die optimale Entscheidung eines Spielers von dessen Einschätzungen abhängen. In Spiel 1 ist sie jedoch unabhängig davon, da U' von O' strikt dominiert wird.[3]

Beispiel II

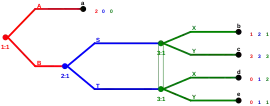
Spiel 2; Dieses Spiel hat ein echtes Teilspiel, beginnend am Knoten (2:1).

Spiel 2 hat nun ein echtes Teilspiel mit dem Nash-Gleichgewicht ${\begin{aligned}(S,Y)\end{aligned}}$ . Das gesamte Spiel hat also mit ${\begin{aligned}(B,S,Y)\end{aligned}}$ ein eindeutiges teilspielperfektes Gleichgewicht. Zusammen mit der Einschätzung $p=1$ genügt diese Strategie den Forderungen 1 bis 3. Forderung 4 ist trivialerweise erfüllt, da es keine Informationsmengen außerhalb des Gleichgewichtspfades gibt. Demnach ist ${\begin{aligned}((B,S,Y),p=1)\end{aligned}}$ also ein perfekt bayessches Gleichgewicht.

Die Strategie ${\begin{aligned}(A,S,X)\end{aligned}}$ ist auch ein Nash-Gleichgewicht, da kein Spieler einen Anreiz zum Abweichen hat. Mit der Einschätzung $p=0$ genügt sie außerdem den Forderungen 1 bis 3, obwohl das Gleichgewicht nicht teilspielperfekt ist.

Gegeben dieser Einschätzungen verhält sich Spieler 3 dann sequentiell rational, wenn er die Strategie X wählt. Allerdings ist die Einschätzungen nicht konsistent mit der Strategie von Spieler 2. Hier greift nun Forderung 4, welche besagt, dass auch außerhalb des Gleichgewichtspfades die Einschätzungen gemäß der bayesschen Regel gebildet werden müssen, wann immer dies möglich ist. Spieler 3 muss somit die Einschätzungen $p=1$ haben, wenn Spieler 2 die Strategie S wählt. Dies ist ein Widerspruch. ${\begin{aligned}((A,S,X),p=0)\end{aligned}}$ genügt also nicht den Forderungen 1 bis 4 und ist somit kein perfekt bayessches Gleichgewicht.[3]

Allerdings ist es umstritten, wann die bayesschen Regel außerhalb des Gleichgewichtspfades angewandt werden kann. Streng genommen wäre dies hier nicht möglich, da die Informationsmenge mit Wahrscheinlichkeit 0 erreicht wird und die bayessche Regel eine Division durch 0 erfordern würde.[4]

Die Bedeutung von „wann immer möglich“

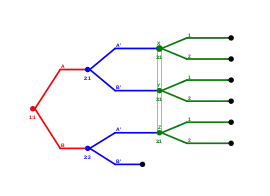
Spiel 3; Spieler 3 hat eine Informationsmenge, die drei Knoten umfasst.

Die sehr vage Formulierung von Forderung 4 besagt, dass die Einschätzungen außerhalb des Gleichgewichtspfades wann immer möglich mit dem Satz von Bayes gebildet werden. Dies zeigt sich besonders für Spiele in Extensivform.

Spiel 3 zeigt, dass es hier nicht ganz eindeutig ist, wie wann immer möglich exakt interpretiert werden soll. Spieler 1 (Rot) könnte hier beispielsweise die Strategie B verfolgen, während Spieler 2 (Blau) die Strategie (B',B') verfolgt. Das bedeutet, dass Spieler 2 an beiden seiner Entscheidungsknoten die Aktion B' wählt.

Gegeben diesen Strategien wird die Informationsmenge von Spieler 3 (Grün) nie erreicht. Sie befindet sich damit außerhalb des Gleichgewichtspfades. Man könnte nun argumentieren, dass die Einschätzungen an den Punkten X, Y und Z frei wählbar sein sollten, da die Informationsmenge gegeben der Gleichgewichtsstrategien mit Wahrscheinlichkeit 0 erreicht wird und sich die bayessche Regel darauf nicht anwenden lässt.

Allerdings könnte man auch fordern, dass die Einschätzungen im Spielverlauf aktualisiert werden sollten, falls ein betroffener Spieler neue Informationen bekommt. Sollte Spieler 3 unerwartet feststellen, dass seine Informationsmenge erreicht wird, so muss er seine Einschätzungen auch entsprechend anpassen.

Ob nun X oder Y eher erreicht wird ist davon abhängig, wie anfällig das Gleichgewicht gegenüber Fehlern der Spieler ist. Um dies zu untersuchen, schlug Reinhard Selten 1975 das Konzept des trembling-hand-perfektes Gleichgewichtsein. Die Grundidee dieses Ansatzes ist, dass jeder Spieler jede Aktion mit mindestens einer geringen positiven Wahrscheinlichkeit wählt, da seine Hand bei der Wahl seiner Strategie zu „zittern“ (engl. to tremble) anfangen könnte. Prinzipiell ist also jeder Knoten des Spielbaumes erreichbar.

Sollte Spieler 1 unbeabsichtigt die Strategie A spielen, wird der Knoten Y erreicht, da Spieler 2 die Strategie (B',B') verfolgt. Damit X erreicht wird, müssten beide Spieler einen Fehler begehen. Gemäß der bayesschen Regel ist es also prinzipiell wahrscheinlicher, dass Knoten Y erreicht wird. Allerdings lässt sich hier trotzdem keine Aussage über die Relationen zu der Einschätzung, sich an Knoten Z zu befinden, treffen.

Es zeigt sich also, dass es im Rahmen des perfekt bayesschen Gleichgewichts keine abschließende Definition von „wann immer möglich“ gibt, die auf den allgemeinen Fall übertragen werden kann. Folglich muss dies wohl bei jeden Spiel separat und möglicherweise auch intuitiv untersucht werden.[5][4]

Eine mögliche Lösung für dieses Problem wäre das von Kreps und Wilson 1982 formulierte sequentielle Gleichgewicht. Dieses geht ähnlich wie das trembling-hand-perfekte Gleichgewicht von einer Folge vollständig gemischter Strategien aus. Die Idee hinter diesem Ansatz ist, eine vollständig gemischte Strategie zu finden, die gegen die eigentliche Gleichgewichtsstrategie konvergiert. Da so alle Informationsmengen mit einer strikt positiven Wahrscheinlichkeit erreicht werden, wäre die bayessche Regel immer anwendbar. Da diese Methode in ihrer Anwendung allerdings sehr kompliziert ist, genügt es in den meisten Fällen, sich auf das perfekt bayessche Gleichgewicht zu beschränken.[6]

Verfeinerung des perfekt bayesschen Gleichgewichts

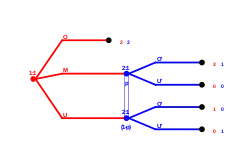
Spiel 4; Die Strategie U wird von O strikt dominiert.

Das Konzept des perfekt bayesschen Gleichgewichts kann noch weiter verfeinert werden, indem man eine zusätzliche Forderung einführt.

Forderung 5:

Jeder Spieler muss an Knoten, welche außerhalb des Gleichgewichtspfades liegen und welche nur erreicht werden, wenn ein anderer Spieler eine strikt dominierte Strategie spielt, die Einschätzung $p=0$ haben, wenn dies möglich ist.

Im Rahmen des perfekt bayesschen Gleichgewichts wird davon ausgegangen, dass die Spieler niemals eine strikt dominierte Strategie spielen werden, ausgehend von einer beliebigen Informationsmenge (Forderung 2). Es ist auf der anderen Seite also auch nicht sinnvoll, dass ein Spieler glaubt, dass ein anderer Spieler eine solche Strategie wählen würde. Auf dem Gleichgewichtspfad verhindert Forderung 3 solche inkonsistenten Einschätzungen. Außerhalb des Gleichgewichtspfades ist das ganze problematischer, da hier Forderung 4 nicht in jedem Fall greift.

In dem dargestellten Spiel gibt es zwei perfekt bayessche Gleichgewichte, die die Forderungen 1 bis 4 erfüllen und zwar ${\begin{aligned}((M,O'),p=1)\end{aligned}}$ und ${\begin{aligned}((O,U'),p\leq \ 0,5)\end{aligned}}$ . Da beim zweiten Gleichgewicht die Informationsmenge außerhalb des Gleichgewichtspfades liegt und Forderung 4 keine Restriktionen macht, können die Einschätzungen hier frei gewählt werden.

Die Strategie U wird allerdings von O strikt dominiert. Es ist also von Spieler 2 nicht sinnvoll zu glauben, dass Spieler 1 U spielen würde. Falls U gespielt wird sollte folglich auch die Einschätzung an den folgenden Knoten zu sein, $(1-p)=0$ betragen. Dies bedeutet im Umkehrschluss, dass $p=1$ sein muss. Das einzige Gleichgewicht, das die Forderungen 1 bis 5 erfüllt, ist demnach ${\begin{aligned}((M,O'),p=1)\end{aligned}}$ .

Eine Ausnahme liegt vor, wenn sowohl U als auch M strikt dominiert wären. In diesem Fall sind die Einschätzungen wieder frei wählbar, da $p$ und $(1-p)$ nicht gleichzeitig gleich 0 sein können.[3]

Es lässt sich auch hier darüber streiten, wie sinnvoll diese fünfte Forderung wirklich ist. Sollte Spieler 2 trotz der Gleichgewichtsstrategie O von Spieler 1 feststellen, dass seine Informationsmenge erreicht wird, muss er davon ausgehen, dass Spieler 1 einen Fehler gemacht hat. In diesem Fall könnte Spieler 1 auch ebenso gut aus Versehen die strikt dominierte Stratagie U gewählt haben, was dafür sprechen würde, dass die Einschätzungen hier frei wählbar sein sollten. Dieser Ansatz übersteigt jedoch die Erklärungskraft des perfekt bayesschen Gleichgewichts. Um hier zu einer abschließenden Lösung zu kommen, müsste man wieder auf die strengeren Konzepte des trembling-hand-perfekten Gleichgewichts oder des sequentiellen Gleichgewichts zurückgreifen.

Signalspiele

Signalspiele sind bayessche Spiele, bei denen die von einem Spieler ausgesandte Signale die Entscheidung eines Gegenspielers beeinflussen. In einem einfachen Signalspiel gibt es zwei Spieler, nämlich einen „Sender“ und einen „Empfänger“. Zu Beginn entscheidet ein Naturzug über den Typ des Senders, wobei davon ausgegangen wird, dass die Wahrscheinlichkeitsverteilung Common Knowledge ist. Der Sender lernt anschließend seinen Typ und kann nun ein bestimmtes Signal wählen. Der Empfänger beobachtet das Signal des Senders, aber nicht seinen Typ, und kann daraufhin ebenfalls eine Aktion wählen. Es liegt also eine asymmetrische Informationsverteilung vor, da der Sender private Informationen über seinen Typ hat.

Die möglichen Strategien des Senders lassen sich in pooling und separierend unterteilen. Eine Pooling-Strategie liegt vor, wenn alle Typen das gleiche Signal wählen. Separierend ist eine Strategie, wenn jeder Typ ein anderes Signal aussendet. Schicken nur manche Typen unterschiedliche Signale, nennt sich die Strategie semi-separierend.[3]

Das Bier-Quiche-Spiel

Spiel 5; Bier-Quiche-Spiel nach Cho und Kreps.

Ein sehr bekanntes Signalspiel ist das Bier-Quiche-Spiel von Cho und Kreps (1987). Die Idee des Spiels lässt sich wie folgt beschreiben:

In einer Bar sitzt ein Schläger (Spieler 2), der sich mit einem anderen Mann (Spieler 1) prügeln möchte. Spieler 1 kennt seinen Typ und weiß auch, dass sich Spieler 2 mit ihm prügeln möchte. Wenn es möglich ist, möchte Spieler 1 unabhängig von seinem Typ das Duell vermeiden. Spieler 1 weiß außerdem, dass seine Bestellung einen Einfluss auf die Entscheidung von Spieler 2 haben wird. Spieler 1 muss also versuchen glaubhaft zu signalisieren, dass er ein Macho ist, um dem Duell zu entgehen. Spieler 2 weiß dagegen nicht, ob Spieler 1 ein „Softie“ oder ein „Macho“ ist, jedoch kennt er die Wahrscheinlichkeitsverteilung. Spieler 2 zieht nur einen Nutzen aus dem Duell, wenn Spieler 1 ein Softie ist, da er andernfalls selbst verprügelt wird. Spieler 2 will deshalb beobachten, was sich Spieler 1 an der Bar bestellt, um so Rückschlüsse auf seinen Typ ziehen zu können. Er weiß, dass sich Machos am liebsten Bier bestellen, Softies hingegen Quiche bevorzugen.

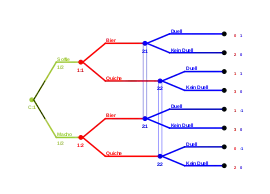
Spiel 5 stellt das Spiel mit der beispielhaften Wahrscheinlichkeit $p=(1/2)$ als Spielbaum dar. Spieler 1 (Sender) hat hier die reinen Strategien (Bier, Bier), (Quiche, Quiche), (Bier, Quiche) und (Quiche, Bier). Die erste (zweite) Aktion wird demnach gespielt, falls die Natur den Typ „Softie“ (Typ „Macho“) für Spieler 1 wählt. Die ersten beiden Strategien des Senders sind Pooling-Strategien, da beide Typen das gleiche Signal aussenden. Die beiden letzten sind separierende Strategien.

Spieler 2 (Empfänger) hat die reinen Strategien (Duell, Duell), (Duell, Kein Duell), (Kein Duell, Duell) und (Kein Duell, Kein Duell). Die erste (zweite) Aktion wird gewählt, falls Spieler 2 Bier (Quiche) beobachtet.

In der Analyse des Spiels zeigt sich, dass es hier keine separierenden Gleichgewichte geben kann, da Spieler 1, falls er ein Softie ist, immer einen Anreiz zum Abweichen hätte. Bei einer separierenden Strategie kann Spieler 2 anhand der Bestellung von Spieler 1 direkt auf seinen Typ zurückschließen. Folglich würde er mit dem Softie immer ein Duell beginnen und mit dem Macho nicht. Da Spieler 1 dem Duell nach Möglichkeit entgehen möchte, hätte er als Softie also einen Anreiz, die jeweils andere Bestellung zu wählen.

Es gibt allerdings zwei perfekte bayessche Gleichgewichte, welche beide Pooling-Gleichgewichte sind, nämlich:

{\begin{aligned}\left(\left([{\text{Bier}},{\text{Bier}}],[{\text{kein Duell}},{\text{Duell}}]\right),p\leq \ 0{,}5\ ,q\geq \ 0{,}5\right)\\\left(\left([{\text{Quiche}},{\text{Quiche}}],[{\text{Duell}},{\text{kein Duell}}]\right),p\geq \ 0{,}5\ ,q\leq \ 0{,}5\right)\end{aligned}}

$p$ ist dabei die bedingte Wahrscheinlichkeit $\operatorname {prob} ({\text{Softie}}\mid {\text{Bier}})$ und $q$ ist $\operatorname {prob} ({\text{Softie}}\mid {\text{Quiche}})$ .

Auch wenn das zweite Pooling-Gleichgewicht wenig intuitiv erscheint, erfüllt es trotzdem die Forderungen 1 bis 5. Durch das intuitive Kriterium von Cho und Kreps lässt sich allerdings auch dieses Gleichgewicht eliminieren.[7][4]

Literatur

Robert Gibbons: A Primer in Game Theory. Financial Times, Harlow 1992, ISBN 0-7450-1159-4.
Ken Binmore: Fun and Games: A Text on Game Theory. D.C. Heath and Company, Lexington, Massachusetts 1992, ISBN 0-669-24603-4.
Drew Fudenberg, Jean Tirole: Game Theory. The MIT Press, Cambridge, Massachusetts 1991, ISBN 0-262-06141-4.
Martin J. Osborne, Ariel Rubinstein: A Course in Game Theory. The MIT Press, Cambridge, Massachusetts 1994, ISBN 0-262-15041-7.
Manfred J. Holler, Gerhard Illing: Einführung in die Spieltheorie. Springer, Berlin Heidelberg 2008, ISBN 978-3-540-69372-7.
Gonzáles-Días, Julio; Meléndez-Jiménez, Miguel A.: On the Notion of Perfect Bayesian Equilibrium. Departamento de Estadística e Investigación Operativa, Universidad de Santiago de Compostela; Departamento de Teoría e Historia Económica, Universidad de Málaga.
Battigalli, Pierpaolo: Strategic Independence and Perfect Bayesian Equilibria. Department of Economics, Princeton University, Princeton, New Jersey 1995.

Weblinks

Enzyklopädie zur Spieltheorie – Projekt der Uni München zum Thema Spieltheorie

Einzelnachweise

Drew Fudenberg, Jean Tirole: Game Theory. The MIT Press, Cambridge, Massachusetts 1991, ISBN 0-262-06141-4, S. 321–323.
Ken Binmore: Fun and Games: A Text on Game Theory. D.C. Heath and Company, Lexington, Massachusetts 1992, ISBN 0-669-24603-4, S. 501–503.
Robert Gibbons: A Primer in Game Theory. Financial Times, Harlow 1992, ISBN 0-7450-1159-4, S. 175–182.
Manfred J. Holler, Gerhard Illing: Einführung in die Spieltheorie. Springer, Berlin, Heidelberg 2008, ISBN 978-3-540-69372-7, S. 110–124.
Gonzáles-Días, Julio; Meléndez-Jiménez, Miguel A.: On the Notion of Perfect Bayesian Equilibrium. Departamento de Estadística e Investigación Operativa, Universidad de Santiago de Compostela; Departamento de Teoría e Historia Económica, Universidad de Málaga. Verfügbar auf: Archivierte Kopie (Memento des Originals vom 12. August 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/eio.usc.es
Dynamische Spiele mit unvollständiger Information. (PDF; 735 kB) (Nicht mehr online verfügbar.) Ehemals im Original; abgerufen am 12. Dezember 2011.@1@2 (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.
Das Bier-Quiche-Spiel (mathematik.uni-muenchen.de). Abgerufen am 17. Dezember 2011.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[FudenbergTiroleGameTheory-1] Drew Fudenberg, Jean Tirole: Game Theory. The MIT Press, Cambridge, Massachusetts 1991, ISBN 0-262-06141-4, S. 321–323.

[2] Ken Binmore: Fun and Games: A Text on Game Theory. D.C. Heath and Company, Lexington, Massachusetts 1992, ISBN 0-669-24603-4, S. 501–503.

[GibbonsGameTheory-3] Robert Gibbons: A Primer in Game Theory. Financial Times, Harlow 1992, ISBN 0-7450-1159-4, S. 175–182.

[HollerIllingSpieltheorie-4] Manfred J. Holler, Gerhard Illing: Einführung in die Spieltheorie. Springer, Berlin, Heidelberg 2008, ISBN 978-3-540-69372-7, S. 110–124.

[5] Gonzáles-Días, Julio; Meléndez-Jiménez, Miguel A.: On the Notion of Perfect Bayesian Equilibrium. Departamento de Estadística e Investigación Operativa, Universidad de Santiago de Compostela; Departamento de Teoría e Historia Económica, Universidad de Málaga. Verfügbar auf: Archivierte Kopie (Memento des Originals vom 12. August 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/eio.usc.es

[6] Dynamische Spiele mit unvollständiger Information. (PDF; 735 kB) (Nicht mehr online verfügbar.) Ehemals im Original; abgerufen am 12. Dezember 2011.@1@2 (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.

[7] Das Bier-Quiche-Spiel (mathematik.uni-muenchen.de). Abgerufen am 17. Dezember 2011.