Bayes-Spiel

Ein Bayes-Spiel (IPA: [ˈbɛɪ̯zˌʃpiːl], ), bayessches Spiel, oder bayesianisches Spiel, bezeichnet in der Spieltheorie ein Spiel mit unvollständiger Information, welches nach dem englischen Mathematiker Thomas Bayes benannt ist. Der Satz von Bayes, mit dessen Hilfe man bedingte Wahrscheinlichkeiten berechnen kann, bildet die Grundlage für Lösungskonzepte dieser Spielart.

Bayes-Spiele sind als Spiele mit imperfekter Information modellierbar.

Definition

In einem Spiel mit unvollständiger Information gibt es mindestens einen Spieler, welcher nicht sämtliche, für das Spiel entscheidende Informationen (i. A. Auszahlungsfunktionen) über die anderen Spieler besitzt. Bayes-Spiele sind damit a Priori nicht analysierbar. Es müssen Vermutungen über die Strategien und Entscheidungen der anderen Spieler in Form von Wahrscheinlichkeitsverteilungen (beliefs) aufgestellt werden.

Nach einem Modell von Harsanyi[1][2] werden Bayes-Spiele mit Hilfe solcher beliefs als Spiele mit imperfekter Information dargestellt und analysiert. In einem solchen Spiel gibt es mindestens einen Spieler, welchem nicht jede zuvor getroffene Entscheidung (sowohl anderer Spieler als auch Zufallsentscheidungen) bekannt ist. Für alle nicht von Spielern getroffenen Zufallsentscheidungen wird ein neuer Spieler (Natur genannt) eingeführt, der diese vor allen anderen Entscheidungen trifft. Somit können dieselben Lösungskonzepte wie bei Spielen mit imperfekter Information angewendet werden.

Beispielsweise ist in Kartenspielen die Verteilung der Karten zufällig und damit in den meisten Fällen unbekannt. Betrachtet man die Verteilung der Karten als ersten Zug des Spielers Natur, so haben die Spieler imperfekte Information über die bisher getroffenen Entscheidungen. Im Gegensatz dazu ist Schach ein klassisches Beispiel für Spiele mit perfekter Information.

Dabei gilt formal für ein Spiel $G=<N;\;<T_{i};\;S_{i};\;u_{i};\;p_{i}>_{i\in N}>$ :

N bezeichnet die Menge der Spieler
$T_{i}$ bezeichnet die möglichen Typen des Spielers i. Dabei ist $t_{i}$ der von der Natur gewählte Typ, $t_{-i}$ sind die Typen aller anderen Spieler.
$S_{i}$ ist die Menge aller möglichen Strategien von Spieler i. Dabei ist $s_{i}$ eine gewählte Strategie und $s_{-i}$ sind die Strategien aller anderen Spieler.
$u_{i}(s_{i};\;s_{-i};\;t_{i};\;t_{-i})$ ist die Auszahlungsfunktion für Spieler i. Diese ist abhängig von allen gewählten Strategien und Typen.
$p_{i}$ sind die beliefs des Spielers i.

Ein Gleichgewicht besteht aus der Strategie jedes Spielers und deren beliefs. Eine Strategie ist eine Menge von Aktionen für jeden möglichen Typ.

Mathematische Grundlagen (Satz von Bayes)

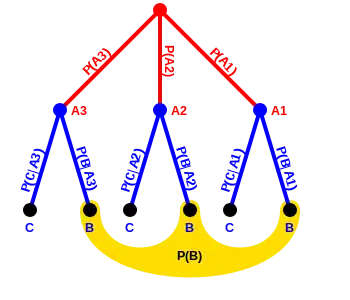
Graphische Veranschaulichung des Bayes-Theorems

Mit Hilfe des Satzes von Bayes lassen sich bedingte Wahrscheinlichkeiten berechnen:

P(A_{i}|B)\;=\;{\frac {P(B|A_{i})\cdot P(A_{i})}{P(B)}}

Dabei gilt für die Wahrscheinlichkeit von $A_{i}$ bedingt $B$ :

{\begin{aligned}P(A_{i}|B)\;&=\;{\frac {P(A_{i}\cap B)}{P(B)}}\\&=\;{\frac {{\frac {P(A_{i}\cap B)}{P(A_{i})}}\cdot P(A_{i})}{P(B)}}\\&=\;{\frac {P(B|A_{i})\cdot P(A_{i})}{P(B)}}\end{aligned}}

Anschaulich also – wie im Bild rechts – ist die Wahrscheinlichkeit, dass $A_{i}$ (rot) eintrifft, unter dem Wissen, dass $B$ eingetroffen ist (gelber Bereich), gerade der Anteil des über $A_{i}$ zu $B$ führenden Astes an allen zu $B$ führenden Ästen.

Nicht-sequentielle Spiele und sequentielle Spiele

Sequentielle Spiele sind runden-basierte Spiele, bei denen die Auszahlungen der Spieler gerade die Summen der Auszahlungen der Spieler in jeder Runde sind. Sind in jeder Runde die Strategiemengen und Auszahlungsfunktionen identisch, spricht man auch von wiederholten Spielen. Dies ist jedoch keine Voraussetzung für sequentielle Spiele.

Je nach Spielart eignen sich unterschiedliche Darstellungsformen. Üblicherweise verwendet man die Normalform nur für nicht-sequentielle Spiele. Die Extensivform wird hingegen sowohl für nicht-sequentielle als auch für sequentielle Spiele benutzt.

Signalspiele bezeichnen eine besondere Art sequentieller Bayes-Spiele, die meist in einer Variante der Extensivform dargestellt werden.

Stochastische Bayes-Spiele modellieren sequentielle Bayes-Spiele mit Umgebungszuständen und stochastischen Zustandsübergängen.[3]

Bayessches Nash-Gleichgewicht

Beispiel 1: nicht sequentielles Bayes-Spiel mit Spielertypen

Das bayessche Nash-Gleichgewicht ist eine Strategiekombination (falls vorhanden), bei der kein Spieler seine erwartete Auszahlung durch einen Strategiewechsel verbessern kann. Dabei muss er seine Vermutungen über die Wahrscheinlichkeitsverteilung (beliefs) für die Strategien der anderen Spieler berücksichtigen. Dieses Konzept ist analog zum Nash-Gleichgewicht im Fall von Spielen mit perfekter und vollständiger Information.

Beispiel

In diesem Spiel planen zwei Arbeitskollegen ihre Freizeitbeschäftigung. Dabei stehen die Möglichkeiten Schwimmbad und Kino zur Wahl. Spieler 1 geht lieber in das Kino, Spieler 2 würde das Schwimmbad vorziehen. Natürlich verbringen beide ihre Freizeit lieber mit einem Freund als mit einem Feind. Allerdings weiß Spieler 2 nicht, wie sehr Spieler 1 ihn mag.

Spieler 1 ist entweder vom Typ Freund oder Feind und er selbst kennt seinen Typ. Die Auszahlungen sind abhängig von ihrem Verhältnis zueinander und der Wahl der Freizeitbeschäftigung: Sind sie Freunde und besuchen die gleiche Einrichtung, erhalten sie eine Auszahlung von 3. Sind sie Feinde möchten sie sich lieber meiden und erhalten eine Auszahlung von 3, wenn sie nicht am selben Ort sind. Zusätzlich erhalten sie die Auszahlung 2 für die bevorzugte Freizeitbeschäftigung.

Die Wahrscheinlichkeitsverteilung über die Typen von Spieler 1 ist common knowledge und gleichverteilt: $P({\text{Freund}})=P({\text{Feind}})={\tfrac {1}{2}}$ . Da die Spieler gleichzeitig entscheiden (keine Absprache möglich), muss Spieler 2 Vermutungen über die Wahl von Spieler 1 aufstellen.

Es gibt zwei bayessche Nash-Gleichgewichte, bei denen sich kein Spieler durch Abweichen von seiner Strategie besser stellen kann.

Im ersten Gleichgewicht mit ([Kino, Schwimmbad]; Kino) gilt gerade P(Kino|Freund)=1 und P(Schwimmbad|Feind)=1. Damit folgt nach Bayes P(Freund|Kino)=P(Feind|Schwimmbad)=1. Analoges Vorgehen im zweiten Gleichgewicht mit ([Schwimmbad, Kino]; Schwimmbad) liefert insgesamt:

${\begin{aligned}&([{\text{Kino}},{\text{Schwimmbad}};&{\text{Kino}})&;{\text{ mit }}P({\text{Freund}}|{\text{Kino}})=P({\text{Feind}}|{\text{Schwimmbad}})=1\;)\\&([{\text{Schwimmbad}},{\text{Kino}};&{\text{Schwimmbad}})&;{\text{ mit }}P({\text{Feind}}|{\text{Kino}})=P({\text{Freund}}|{\text{Schwimmbad}})=1\;)\\\end{aligned}}$

Perfekt bayessches Gleichgewicht

Das perfekt bayessche Gleichgewicht ist eine Weiterentwicklung des teilspielperfekten Gleichgewichts für Spiele mit unvollständiger Information.

Eine Menge von Strategien und Vermutungen über Wahrscheinlichkeitsverteilungen (beliefs) nennt man perfekt bayessches Gleichgewicht, wenn folgende Voraussetzungen erfüllt sind:

Jeder Spieler muss für jede Informationsmenge beliefs angeben können, welche jedem Knoten dieser Menge eine Wahrscheinlichkeit zuordnet.
Jeder Spieler handelt, gegeben seiner beliefs und der Strategie der Gegner, rational. Das heißt, die Strategien führen zu teilspielperfekten Ergebnissen.
Die beliefs auf dem Gleichgewichtspfad werden mit Hilfe des Bayes-Theorems ermittelt.

Bemerkung: Diese Forderungen definieren streng genommen nur ein schwach perfektes bayessches Gleichgewicht. Für ein perfekt bayessches Gleichgewicht bedarf es einer weiteren Bedingung.

Beispiel 1

Beispiel 1: Bier-Quiche Spiel

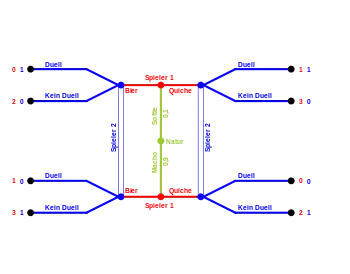
Im sogenannten Bier-Quiche-Spiel (erstmals von Cho und Kreps behandelt[4]) gibt es zwei Spieler:

Spieler 1 ist entweder ein Softie oder ein Macho. Von welchem Typ Spieler 1 ist, wird von der Natur vorgegeben und ist nur ihm selbst bekannt. Dabei kennen beide Spieler die Wahrscheinlichkeitsverteilung: $P(Softie)=0,1$ und $P(Macho)=0,9$ . Er hat die Wahl zum Frühstück Bier oder Quiche zu bestellen. Als Softie erhält er durch Quiche eine Auszahlung von 1 und durch Bier 0, als Macho umgekehrt.

Spieler 2 trifft später Spieler 1 und hat die Möglichkeit sich zu duellieren. Er möchte sich jedoch nur duellieren, falls Spieler 1 ein Softie ist. Jedoch kennt Spieler 2 von Spieler 1 nicht den Typ, sondern nur dessen Frühstücksbestellung (Signal). Spieler 1 möchte in keinem Fall ein Duell und bekommt für kein Duell immer Auszahlung 2. Spieler 2 bekommt Auszahlung 1, falls er sich mit einem Softie duelliert oder das Duell mit einem Macho meidet. In allen anderen Fällen erhält er Auszahlung 0.

Die Graphik rechts veranschaulicht dieses Signalspiel mit aufaddierter Auszahlung.

Mögliche Strategien für Spieler 1 sind:

Spiele Bier egal ob Macho oder Softie, kurz: [Bier, Bier],
Spiele Quiche egal ob Macho oder Softie: [Quiche, Quiche],
Spiele Bier als Macho und Quiche als Softie: [Bier, Quiche] und
Spiele Quiche als Macho und Bier als Softie: [Quiche, Bier].

Mögliche Strategien für Spieler 2 sind:

Spiele immer Duell, egal welches Signal, kurz: [Duell, Duell],
Spiele immer Kein Duell, egal welches Signal: [Kein Duell, Kein Duell],
Spiele Duell, falls Signal Bier, sonst Kein Duell: [Duell, Kein Duell] und
Spiele Kein Duell, falls Signal Bier, sonst Duell: [Kein Duell, Duell].

Es gibt zwei perfekt bayessche Gleichgewichte:

Im ersten Gleichgewicht mit ([Quiche, Quiche]; [Duell, Kein Duell]), gilt P(Quiche|Softie) = P(Quiche|Macho) = 1. Mit dem Bayes-Theorem ergibt sich gemäß Forderung 3 der belief von Spieler 2:

$P(Softie|Quiche)={\frac {P(Quiche|Softie)\cdot P(Softie)}{P(Quiche)}}={\frac {1\cdot 0,1}{1}}=0,1$ .

Analog ergibt sich im zweiten Gleichgewicht ([Bier, Bier]; [Kein Duell, Duell]) die beliefs $P(Softie|Bier)=0,1$ .

Insgesamt gilt also:

${\begin{aligned}&((&[Quiche&,Quiche]&;\;[Duell,Kein\;Duell])&;\;P(Softie|Quiche)=0,1){\text{ und}}\\&((&[Bier&,Bier]&;\;[Kein\;Duell,Duell])&;\;P(Softie|Bier)=0,1)\end{aligned}}$

Beide Gleichgewichte erfüllen zwar die Bedingungen an ein perfekt bayessches Gleichgewicht, Cho und Kreps erweitern aber den Gleichgewichtsbegriff um eine weitere Forderung. Im Allgemeinen wird diese intuitives Kriterium genannt und sorgt dafür, dass das erste Gleichgewicht ausgeschlossen wird[5].

Beispiel 2

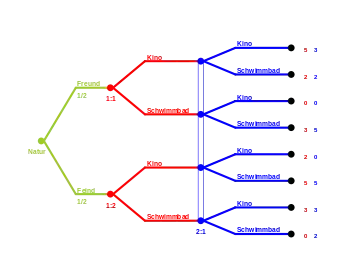
Dieses Beispiel veranschaulicht, wie beliefs im Laufe eines wiederholten Spiels mit Hilfe des Bayes-Theorems angepasst werden. Es gibt nur einen Spieler, der auf das Ergebnis eines eventuell manipulierten Münzwurfs wettet. Eine richtige Voraussage bringt eine Auszahlung von 1, ansonsten 0. Die möglichen Münztypen werden von der Natur vorgegeben und sind gleich wahrscheinlich: Immer Kopf (IK), Faire Münze (FM) und Immer Zahl (IZ).

In der ersten Runde setzt der Spieler seine beliefs entsprechend der Wahrscheinlichkeitsverteilung der Typen auf (1/3; 1/3; 1/3) für (IK; FM; IZ). Zunächst bringt Strategie Kopf dieselbe erwartete Auszahlung wie Strategie Zahl. Der Spieler setzt also beliebig auf Kopf oder Zahl und wirft anschließend die Münze. Bevor er ein weiteres Mal setzt, passt er seine beliefs mit Hilfe des Bayes-Theorems an:

Kopf (K) wird geworfen:

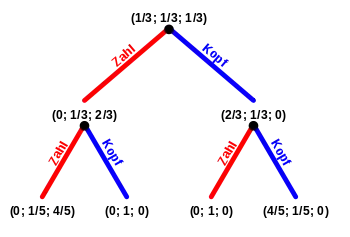
Änderung der beliefs in Abhängigkeit vom Ereignis

${\begin{aligned}P(IK|K)&={\frac {P(K|IK)\cdot P(IK)}{P(K)}}&&={\frac {1\cdot 1/3}{1/2}}&&={\frac {2}{3}}\\P(FM|K)&={\frac {P(K|FM)\cdot P(FM)}{P(K)}}&&={\frac {1/2\cdot 1/3}{1/2}}&&={\frac {1}{3}}\\P(IZ|K)&={\frac {P(K|IZ)\cdot P(IZ)}{P(K)}}&&={\frac {0\cdot 1/3}{1/2}}&&=0\\\end{aligned}}$

Zahl (Z) wird geworfen:

${\begin{aligned}P(IK|Z)&={\frac {P(Z|IK)\cdot P(IK)}{P(Z)}}&&={\frac {0\cdot 1/3}{1/2}}&&=0\\P(FM|Z)&={\frac {P(Z|FM)\cdot P(FM)}{P(Z)}}&&={\frac {1/2\cdot 1/3}{1/2}}&&={\frac {1}{3}}\\P(IZ|Z)&={\frac {P(Z|IZ)\cdot P(IZ)}{P(Z)}}&&={\frac {1\cdot 1/3}{1/2}}&&={\frac {2}{3}}\\\end{aligned}}$

Geht das Spiel weiter, werden die beliefs wie oben angepasst. Dabei ist nur zu beachten, dass sich die Wahrscheinlichkeiten $P(K)$ beziehungsweise $P(Z)$ nach jedem Wurf ändern. Unter der Annahme, dass im ersten Wurf Kopf gefallen ist, gilt:

${\begin{aligned}P(K)&=P(IK|K)\cdot P(IK)+P(FM|K)\cdot P(FM)+P(IZ|K)\cdot P(IZ)={\tfrac {2}{3}}\cdot 1+{\tfrac {1}{3}}\cdot {\tfrac {1}{2}}+0\cdot 0={\tfrac {5}{6}}{\text{ und}}\\P(Z)&=1-P(K)={\tfrac {1}{6}}\end{aligned}}$

Insgesamt setzt der Spieler also im ersten Zug zufällig (gleichverteilt) auf Kopf oder Zahl. Danach wird er solange auf das Ergebnis der ersten Runde setzten, bis das Gegenteilige eintritt. Sofern dieser Fall überhaupt irgendwann eintritt, wird er ab diesem Zeitpunkt seine Strategie wieder zufällig wählen, da es sich mit Sicherheit um eine faire Münze handelt.

Siehe auch

Literatur

Robert Gibbons: A Primer in Game Theory. Financial Times, Harlow 1992, ISBN 0-7450-1159-4.
Drew Fudenberg, Jean Tirole: Game Theory. The MIT Press, Cambridge, Massachusetts 1991, ISBN 0-262-06141-4.
John A. Hartigan: Bayes Theory. Springer, New York, Heidelberg 1983, ISBN 3-540-90883-8.

Einzelnachweise

John C. Harsanyi: Games with Incomplete Information Played by "Bayesian" Players Part I. The Basic Model. In: Management Science. Band 14, Nr. 3, 1967, S. 127–261, doi:10.1287/mnsc.14.3.159, JSTOR:30046151.
Drew Fudenberg, Jean Tirole: Game Theory. The MIT Press, Cambridge, Massachusetts 1991, ISBN 978-0-262-06141-4, S. 209 ff.
Stefano Albrecht, Jacob Crandall, and Subramanian Ramamoorthy. Belief and Truth in Hypothesised Behaviours. Artificial Intelligence, 235, 2016, S. 63–94, doi:10.1016/j.artint.2016.02.004
In-Koo Cho and David M. Kreps: Signaling Games and Stable Equilibria. In: The Quarterly Journal of Economics. Band 102, Nr. 2, 1987, S. 183–187, JSTOR:1885060.
In-Koo Cho and David M. Kreps: Signaling Games and Stable Equilibria. In: The Quarterly Journal of Economics. Band 102, Nr. 2, 1987, S. 185, JSTOR:1885060.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] John C. Harsanyi: Games with Incomplete Information Played by "Bayesian" Players Part I. The Basic Model. In: Management Science. Band 14, Nr. 3, 1967, S. 127–261, doi:10.1287/mnsc.14.3.159, JSTOR:30046151.

[2] Drew Fudenberg, Jean Tirole: Game Theory. The MIT Press, Cambridge, Massachusetts 1991, ISBN 978-0-262-06141-4, S. 209 ff.

[3] Stefano Albrecht, Jacob Crandall, and Subramanian Ramamoorthy. Belief and Truth in Hypothesised Behaviours. Artificial Intelligence, 235, 2016, S. 63–94, doi:10.1016/j.artint.2016.02.004

[4] In-Koo Cho and David M. Kreps: Signaling Games and Stable Equilibria. In: The Quarterly Journal of Economics. Band 102, Nr. 2, 1987, S. 183–187, JSTOR:1885060.

[5] In-Koo Cho and David M. Kreps: Signaling Games and Stable Equilibria. In: The Quarterly Journal of Economics. Band 102, Nr. 2, 1987, S. 185, JSTOR:1885060.