Oszillation (Topologie)

In d​er Mathematik k​ommt der Begriff d​er Oszillation i​n der Topologie vor, e​inem der Teilgebiete d​er Mathematik. Er t​ritt ebenfalls i​n der Analysis u​nd hier insbesondere i​n Integralrechnung auf. Statt v​on der Oszillation spricht m​an auch v​on der Schwankung o​der der Schwankungsbreite. Die Oszillation d​ient bei d​er Untersuchung v​on Stetigkeitsfragen z​u Abbildungen v​on topologischen Räumen i​n metrische Räume dazu, i​n einem gewissen Sinne d​ie Unstetigkeit e​iner Abbildung z​u messen. Mit d​em Begriff d​er Oszillation verwandt i​st der d​es Stetigkeitsmoduls v​on Abbildungen metrischer Räume.[1][2][3][4][5][6][7][8][9]

Oszillation einer Folge

Die Oszillation einer Folge (hier die blauen Punkte) ist die Differenz zwischen dem Limes Superior und dem Limes Inferior

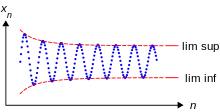
Sei ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ eine Folge reeller Zahlen. Die Oszillation ${\displaystyle \omega (a_{n})}$ ist definiert als Differenz zwischen dem Limes superior und Limes inferior von ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$:

${\displaystyle \omega (a_{n})=\limsup _{n\to \infty }a_{n}-\liminf _{n\to \infty }a_{n}}$.

Die Oszillation einer Folge ist genau dann null, wenn die Folge konvergiert. Die Oszillation ist nicht definiert, wenn Limes Superior und Limes Inferior beide gleichzeitig gleich ${\displaystyle +\infty }$ oder gleich ${\displaystyle -\infty }$ sind, wenn also die Folge bestimmt divergiert.

Definitionen, Sprech- und Schreibweisen

Gegeben sei ein topologischer Raum ${\displaystyle (X,{\mathcal {O}})}$, ein metrischer Raum ${\displaystyle (Y,d_{Y})}$ sowie eine Abbildung ${\displaystyle f\colon X\to Y}$.

Oszillation auf einer Teilmenge

Für eine beliebige nicht-leere Teilmenge ${\displaystyle U\subseteq X}$ versteht man unter der Oszillation von ${\displaystyle f}$ auf ${\displaystyle U}$ bzw. unter der Schwankung von ${\displaystyle f}$ auf ${\displaystyle U}$ den Durchmesser der Bildmenge ${\displaystyle f(U)}$ bezüglich der Metrik ${\displaystyle d_{Y}}$, also diejenige Größe ${\displaystyle {\Omega }_{f}(U)}$, welche folgendermaßen definiert ist:

${\displaystyle {\Omega }_{f}(U):=\operatorname {diam} _{d_{Y}}{f(U)}=\sup\{d_{Y}(f(a),f(b)):a,b\in U\}\in [0,\infty ]}$

Es wird im Allgemeinen auch die Oszillation ${\displaystyle {\Omega }_{f}(U)=\infty }$ nicht ausgeschlossen, wenn – wie im Falle unbeschränkter Funktionen möglich – kein endliches Supremum existiert.

Ein häufig betrachteter Fall ist der, dass ${\displaystyle Y=\mathbb {R} }$ ist, wobei ${\displaystyle d_{Y}}$ die Betragsmetrik, also die durch die Betragsfunktion gegebene darstellt, während zugleich ${\displaystyle f}$ auf ${\displaystyle U}$ beschränkt ist. Unter diesen Gegebenheiten ist

${\displaystyle {\Omega }_{f}(U)=\sup _{x\in U}f(x)-\inf _{x\in U}f(x)}$[10]

Hinsichtlich der Bezeichnung findet man statt ${\displaystyle {\Omega }_{f}(U)}$ auch ${\displaystyle \omega (f,U)}$ oder ${\displaystyle \sigma (f,U)}$; manchmal auch, jedoch eher in englischsprachigen Quellen, ${\displaystyle \operatorname {osc} (f,U)}$.

Oszillation in einem Punkt

In jeder Umgebung um den Punkt p oszilliert die Funktion zwischen f(a) und f(b) unendlich oft. Die Oszillation dieser Funktion an dem Punkt p ist damit f(b)-f(a).

Für einen Punkt ${\displaystyle x\in X}$ definiert man:

${\displaystyle {\omega }_{f}(x):=\inf\{{\Omega }_{f}(U):U\in {\mathcal {U}}_{x}\}\in [0,\infty ]}$[11]

Man nennt diese Größe die Oszillation von ${\displaystyle f}$ im Punkte ${\displaystyle x}$ oder die Oszillation von ${\displaystyle f}$ in (bei) ${\displaystyle x}$ oder auch die Punktschwankung von ${\displaystyle f}$ in (bei) ${\displaystyle x}$. Das obige Infimum wird dabei definitionsgemäß über alle ${\displaystyle x}$-Umgebungen im Umgebungsfilters ${\displaystyle {\mathcal {U}}_{x}}$ gebildet. Es genügt jedoch für dessen Bestimmung auch schon, allein die offenen Umgebungen innerhalb ${\displaystyle {\mathcal {U}}_{x}}$ oder gar nur die ${\displaystyle x}$-Umgebungen einer beliebigen in ${\displaystyle {\mathcal {U}}_{x}}$ enthaltenen Umgebungsbasis zu betrachten.

Statt ${\displaystyle {\omega }_{f}(x)}$ gibt es auch die Schreibung ${\displaystyle {\omega }(x;f)}$ bzw. ${\displaystyle s_{f}(x)}$ . Daneben ist, sofern aus dem Kontext heraus die Abhängigkeit von ${\displaystyle f}$ keiner Hervorhebung bedarf, die einfache Schreibung ${\displaystyle {\omega }(x)}$ bzw. ${\displaystyle s(x)}$ zu finden.

Wird die topologische Struktur von ${\displaystyle (X,{\mathcal {O}})}$ ebenfalls durch eine Metrik ${\displaystyle d_{X}}$ erzeugt, so hat der Umgebungsfilter des Punktes ${\displaystyle x\in X}$ die ${\displaystyle \epsilon }$-Umgebungen ${\displaystyle U_{\epsilon }(x)}$   (${\displaystyle \epsilon >0}$) als Umgebungsbasis und es gilt:

${\displaystyle {\omega }_{f}(x)=\lim _{\epsilon \to 0+}{{\Omega }_{f}(U_{\epsilon }(x))}}$

Untersuchungen zur Oszillation treten oft – etwa in der Integralrechnung – für den Fall auf, dass die betrachteten Funktionen auf reellen Intervallen leben, also ${\displaystyle X=[a,b]\subset \mathbb {R} =Y}$ ist und zugleich ${\displaystyle f:[a,b]\to \mathbb {R} }$ eine beschränkte Funktion ist.

Da für einen Punkt ${\displaystyle x\in \mathbb {R} }$ die offenen Intervalle der Form ${\displaystyle U=(x-\epsilon ,x+\epsilon )\subseteq \mathbb {R} }$ und auch die abgeschlossenen Intervalle der Form ${\displaystyle U=[x-\epsilon ,x+\epsilon ]\subseteq \mathbb {R} }$   ${\displaystyle (\epsilon >0)}$ eine Umgebungsbasis bilden, hat man:

${\displaystyle \omega _{f}(x)=\lim _{\epsilon \to 0+}\Omega _{f}((x-\epsilon ,x+\epsilon )\cap [a,b])=\lim _{\epsilon \to 0+}\Omega _{f}([x-\epsilon ,x+\epsilon ]\cap [a,b])}$.

Beispiel

Die Funktion ${\displaystyle f(x)=\sin \left({\tfrac {1}{x}}\right)}$ für positive ${\displaystyle x}$

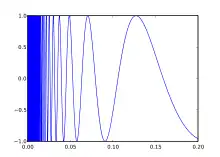
Für d​ie Funktion

${\displaystyle f\colon \mathbb {R} \to \mathbb {R} \colon x\mapsto f(x)={\begin{cases}\sin \left({\tfrac {1}{x}}\right)&;x\neq 0\\0&;x=0\end{cases}}}$

ist ${\displaystyle \omega _{f}(x)=0}$ für ${\displaystyle x\neq 0}$ und ${\displaystyle \omega _{f}(0)=2}$.

Resultate

1. Die Funktion ${\displaystyle {\omega }_{f}\colon x\mapsto {\omega }_{f}(x)\in [0,\infty ]}$ ist eine oberhalb stetige Funktion.
2. Für eine Abbildung von einem topologischen in einen metrischen Raum ist Stetigkeit in einem Punkte gleichbedeutend damit, dass in diesem Punkt die Oszillation gleich Null ist. Mit anderen Worten heißt das für ${\displaystyle x\in X}$ ist ${\displaystyle f}$ in ${\displaystyle x}$ stetig genau dann, wenn ${\displaystyle {\omega }_{f}(x)=0}$ ist. Eine Abbildung von einem topologischen in einen metrischen Raum ist folglich stetig genau dann, wenn sie in keinem Punkte eine Oszillation größer Null aufweist.
3. Bezeichnet man mit ${\displaystyle \Delta (f)}$ die Menge der Unstetigkeitsstellen von ${\displaystyle f}$ und setzt man ${\displaystyle \Delta _{N}(f)=\{x\in X:{\omega }_{f}(x)\geq {\tfrac {1}{N}}\}}$ mit ${\displaystyle N\in \mathbb {N} }$, so gilt

   ${\displaystyle \Delta (f)=\bigcup _{N=1}^{\infty }\Delta _{N}(f)}$.

4. Die ${\displaystyle \Delta _{N}(f)}$ sind allesamt abgeschlossene Mengen und damit ist ${\displaystyle \Delta (f)}$ stets eine F_σ-Menge.
5. Ist ${\displaystyle X=[{\vec {a}},{\vec {b}}]\subset {\mathbb {R} }^{n}}$ ein abgeschlossenes n-dimensionales Intervall und ${\displaystyle f}$ eine beschränkte reelle Funktion, so ist ${\displaystyle f}$ dann und nur dann Riemann-Darboux-integrierbar, wenn die ${\displaystyle \Delta _{N}(f)}$ allesamt Jordan-Nullmengen sind.

Zum Stetigkeitsmodul

→ Hauptartikel: Stetigkeitsmodul

Der mit der Oszillation verwandte Begriff des Stetigkeitsmoduls wurde von Henri Léon Lebesgue im Jahre 1910 eingeführt. Das Stetigkeitsmodul zu einer Abbildung ${\displaystyle f}$ zwischen zwei metrischen Räume ${\displaystyle (X,d_{X})}$ und ${\displaystyle (Y,d_{Y})}$ und einer gegebenen reellen Zahl ${\displaystyle \eta >0}$ ist dabei die folgende Größe ${\displaystyle \omega (f;\eta )}$:

${\displaystyle \omega (f;\eta )=\sup\{d_{Y}(f(a),f(b)):a,b\in X\land d_{X}(a,b)\leq \eta \}\in [0,\infty ]}$[12]

Der Stetigkeitsmodul h​at folgende Eigenschaften:

1. ${\displaystyle \omega (f;0)=0}$.
2. ${\displaystyle \eta \mapsto \omega (f;\eta )}$ ist monoton steigend.
3. ${\displaystyle \eta \mapsto \omega (f;\eta )}$ ist subadditiv.
4. ${\displaystyle \lim _{\eta \to 0}{\omega (f;\eta )}=0}$ ist gleichbedeutend damit, dass ${\displaystyle f}$ gleichmäßig stetig ist.

Siehe auch

• Beschränkte Variation

Literatur

• Hermann Athen, Jörn Bruhn (Hrsg.): Lexikon der Schulmathematik und angrenzender Gebiete. Band 4: S–Z. Aulis Verlag, Köln 1978, ISBN 3-7614-0242-2.
• John J. Benedetto: Real Variable and Integration. B. G. Teubner Verlag, Stuttgart 1976, ISBN 3-519-02209-5.
• Nicolas Bourbaki: Elements of Mathematics. General Topology. Part 2 (= ADIWES International Series in Mathematics). Addison-Wesley Publishing Company, Reading MA 1966.
• Harro Heuser: Lehrbuch der Analysis. Teil 1 (= Mathematische Leitfäden). 16., durchgesehene Auflage. B. G. Teubner Verlag, Stuttgart 2006, ISBN 978-3-8351-0131-9.
• Kazimierz Kuratowski: Topology. New edition, revised and augmented Auflage. Volume 1. Academic Press, New York / London 1966 (Aus dem Französischen übersetzt von J. Jaworowski).
• Serge Lang: Analysis. Hrsg.: Willi Jäger. Inter European Editions, Amsterdam 1977, ISBN 0-201-04152-9 (Deutsche Übersetzung von Bernd Wollring).
• John C. Oxtoby: Measure and Category. A Survey of the Analogies between Topological and Measure Spaces (= Graduate Texts in Mathematics. Band 2). 2. Auflage. Springer Verlag, Berlin u. a. 1987, ISBN 3-540-90508-1.
• Guido Walz [Red.]: Lexikon der Mathematik in sechs Bänden. Band 4. Spektrum Akademischer Verlag, Heidelberg / Berlin 2002, ISBN 3-8274-0436-3.
• Guido Walz [Red.]: Lexikon der Mathematik in sechs Bänden. Band 5. Spektrum Akademischer Verlag, Heidelberg / Berlin 2002, ISBN 3-8274-0437-1.
• Stephen Willard: General Topology. Addison-Wesley, Reading MA u. a. 1970 (MR0264581).

Einzelnachweise und Anmerkungen

1. Lexikon der Mathematik in sechs Bänden. Band 4, S. 128–129.
2. Lexikon der Schulmathematik. Band 4, S. 941–942.
3. H. Heuser: Lehrbuch der Analysis. 2006, S. 241, 470–473.
4. J. J. Benedetto: Real Variable and Integration. 1976, S. 24.
5. S. Lang: Analysis. 1977, S. 403.
6. J. C. Oxtoby: Measure and Category. 1987, S. 31 ff.
7. S. Willard: General Topology. 1970, S. 177.
8. N. Bourbaki: Elements of Mathematics. 1966, S. 151.
9. K. Kuratowski: Topology. 1966, S. 208.
10. Stellenweise wird sogar eine noch allgemeinere Situation zugrundegelegt. Dann betrachtet man in ${\displaystyle (X,{\mathcal {O}})}$ eine nicht-leere Teilmenge ${\displaystyle A\subseteq X}$ sowie eine Abbildung ${\displaystyle f\colon A\to Y}$ und definiert dann ${\displaystyle {\Omega }_{f}(U):=\operatorname {diam_{d_{Y}}} {f(A\cap U)}=\sup\{d_{Y}(f(a),f(b)):a,b\in (A\cap U)\}\in [0,\infty ]}$. Aus Vereinfachungsgründen wird dann bei ${\displaystyle A\cap U=\emptyset }$   ${\displaystyle {\Omega }_{f}(U)=\infty }$ gesetzt. Vgl. hierzu S. Willard: General Topology. 1970, S. 177.
11. Bei N. Bourbaki: Elements of Mathematics. 1966, S. 151. wird diese Größe auch allgemeiner für ${\displaystyle A\subseteq X}$, ${\displaystyle f\colon A\to Y}$ und ${\displaystyle x\in {\overline {A}}}$ definiert.
12. Lexikon der Mathematik in sechs Bänden. Band 5, S. 108.