Nizza-Modell
Das Nizza-Modell (englisch Nice model, Aussprache: [ˈniːs], nach der Stadt Nizza, wo es am Observatoire de la Côte d’Azur entwickelt wurde) ist ein Modell für eine späte Migration der Planeten im Sonnensystem, das 2005 von R. Gomes, H. F. Levison, A. Morbidelli und K. Tsiganis (in alphabetischer Reihenfolge) in drei Nature-Artikeln vorgeschlagen wurde. Das Modell kann etliche Eigenschaften des Sonnensystems vorhersagen.
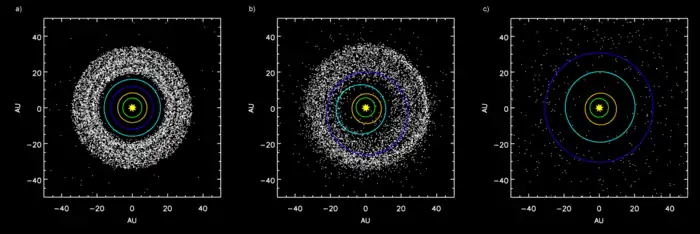
a) vor der Jupiter/Saturn-2:1-Resonanz, b) Zerstreuung der Objekte des Kuipergürtels in das Sonnensystem, nachdem sich die Umlaufbahn Neptuns verschoben hatte, c) nach dem Ausstoß von Objekten des Kuipergürtels durch Jupiter
Das Modell

Das Modell beschreibt eine Migration der Planeten, nachdem sich die protoplanetare Gasscheibe aufgelöst hat. Es ist also kein Migrationsmodell im engeren Sinne wie etwa das Grand-Tack-Modell. Das Nizza-Modell nimmt an, dass die Planeten ursprünglich auf nahezu kreisförmigen, kompakten Bahnorbits liefen. Außerdem nimmt es an, dass bei der Planetenentstehung eine Scheibe von Planetesimalen entstand, die von außerhalb der Planetenorbits bis hinaus zu einer Entfernung von 35 AU reichte und eine Gesamtmasse von etwa 35 Erdmassen hatte.
Die Riesenplaneten des Sonnensystems streuen nun zunächst vereinzelt Planetesimale aus der Scheibe. Dabei wird Drehimpuls übertragen, und die Bahnen der Planeten ändern sich leicht. Mit numerischen Simulationen kann gezeigt werden, dass dadurch Saturn, Uranus und Neptun langsam nach außen wandern und Jupiter nach innen.
Nach ein paar hundert Millionen Jahren (500–800 Mio. Jahre nach Entstehung der Sonne) kommt es zu einer 2:1-Resonanz (englisch mean motion resonance, MMR) zwischen Jupiter und Saturn. Dadurch steigen die Exzentrizitäten, und das System destabilisiert sich. Die Planeten Saturn, Uranus und Neptun kommen einander und der Scheibe aus Planetesimalen nahe. Dadurch werden die Planetesimale praktisch schlagartig zerstreut, ein Teil der Planetesimale fliegt in das innere Planetensystem und löst dort das Große Bombardement aus. In etwa 50 Prozent der simulierten Modelle kommt es dabei auch zu einem Platzwechsel zwischen den zwei äußersten Gasplaneten Uranus und Neptun (siehe die Grafik rechts).[1] Nach etwa hundert Millionen Jahren erreichen die Planeten schließlich ihre heutigen Entfernungen, ihre Exzentrizitäten werden gedämpft und das System stabilisiert sich wieder.
Neben den Positionen, Exzentrizitäten und Inklinationen der Riesenplaneten und dem großen Bombardement erklärt das Modell noch eine Reihe weitere Eigenschaften des heutigen Sonnensystems:
- Während der globalen Instabilität sind die Co-Orbit-Regionen von Jupiter gravitativ offen. Die gestreuten Planetesimale können in dieser Zeit in diese Regionen beliebig hinein und wieder heraus fliegen. Am Ende der Instabilitätsphase sind die Regionen vergleichsweise plötzlich wieder gravitativ geschlossen, und die Objekte, die zu diesem Zeitpunkt dort waren, sind gefangen. Dies erklärt die Jupiter-Trojaner und Hilda-Asteroiden. Analoges gilt auch für die Trojaner von Neptun. Das Modell stimmt in allen wesentlichen Eigenschaften der Trojaner – bis auf deren große Inklinationen – überein.
- Saturn, Uranus und Neptun kamen einander und den Planetesimalen während der globalen Instabilität nahe, daher sind Dreifachstöße zwischen zwei Planeten und einem Planetesimal vergleichsweise wahrscheinlich. Bei solchen Begegnungen wird der Planetesimal von einem der beiden Planeten eingefangen und umkreist diesen fortan als Mond. Da es keine Notwendigkeit gibt, dass der Mond den Planeten in der Äquatorialebene umkreisen sollte, erhält man einen bei den äußeren Planeten häufig vorkommenden irregulären Mond. Dadurch können prinzipiell die irregulären Monde der Riesenplaneten bis auf die des Jupiters erklärt werden. Die Voraussagen stimmen bezüglich Inklination, Exzentrizität und großer Halbachse mit den Beobachtungen überein. Die zunächst vorhergesagte Massenverteilung der Planeten entspricht nicht der gemessenen; dies lässt sich jedoch erklären, wenn man annimmt, dass es zu Kollisionen zwischen den irregulären Monden gekommen ist.
- 99 % der Masse der Planetesimalscheibe geht durch die Stöße verloren – die verbleibenden Körper hingegen bilden den Kuipergürtel. Dabei ist das Modell in der Lage, alle wichtigen Eigenschaften des Kuipergürtels zu erklären, was davor noch keinem Modell gleichzeitig gelungen ist:
- die Koexistenz resonanter und nicht-resonanter Objekte
- die relative Verteilung der großen Halbachse und der Exzentrizität des Kuipergürtels
- die Existenz einer Außenkante in der Entfernung einer 2:1-Resonanz mit Neptun
- die bimodale Verteilung der Objekte und die dabei bestehende Korrelation zwischen der Inklination und den Eigenschaften des Objekts
- die orbitale Verteilung der Plutinos und der 2:5-Libratoren (eine 1975 von Franklin et al. beschrieben Klasse von Asteroiden)[2]
- die Existenz der extended scattered disc
- das Massendefizit des Kuipergürtels.
Kritik und Erweiterung
Das Modell beschreibt nicht die Migration in der protoplanetaren Gasscheibe, sondern setzt erst danach an. Die Probleme und offenen Fragen der klassischen planetaren Migration werden dadurch also nicht gelöst.
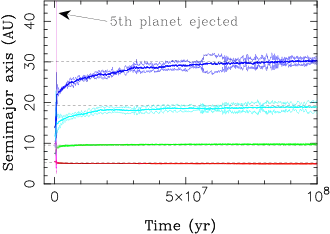
Bei der Entwicklung des Modells wurden nur die vier äußeren Riesenplaneten betrachtet, die Auswirkung auf die Bahnen der terrestrischen Planeten wurden nicht berücksichtigt. In der Instabilitätsphase würden diese jedoch wahrscheinlich gestört werden. Auch neigen derart instabile Systeme dazu, Planeten zu verlieren. Beides kann möglicherweise dadurch vermieden werden, dass man dem System ursprünglich einen weiteren Riesenplaneten hinzufügt, der das System stabilisiert und schließlich selbst aus dem Sonnensystem geworfen wird.
David Nesvorný vom Southwest Research Institute zeigte 2011, dass die Wahrscheinlichkeit dafür wesentlich höher ist als für ein Modell ohne fünften Riesenplaneten. Dabei wurden eine Vielzahl von Simulationen mit unterschiedlichen Anfangsbedingungen, Migrationsraten der Planeten, Auflösungsgeschwindigkeiten der Gasscheibe, Massen der Scheibe aus Planetesimalen und Massen des zusätzlichen Planeten (zwischen 1/3 und 3 Uranusmassen) gemacht und nach vier Kriterien ausgewertet:
- Kriterium A: Am Ende muss das System genau 4 Riesenplaneten haben.
- Kriterium B: Die Planeten müssen am Ende vergleichbare Umlaufbahnen zu den heute beobachtbaren haben. (z. B. max. 20 % Abweichung in der Großen Halbachse).
- Kriterium C: Gewisse Parameter müssen so sein, dass die Möglichkeit zum Einfang irregulärer Monde besteht – wie oben beschrieben.
- Kriterium D: Der Abstand zwischen Jupiter und Saturn muss so sein, dass die inneren terrestrischen Planeten überleben.
Bei der Auswertung stellte man fest, dass das Kriterium A bei anfangs 4 Riesenplaneten in unter 13 % der Simulationen erfüllt ist, während es bei anfangs 5 Planeten bei 37 % der Simulationen erfüllt ist; Kriterium B ist bei 4 Planeten in nur 2,5 % der Fällen erfüllt, während es bei Hinzunahme eines 5. Planeten in 23 % der Fälle erfüllt ist. Bei richtiger Wahl der Masse des fünften Planeten von 1/2 Uranusmasse steigen die Wahrscheinlichkeiten für Kriterium A und B sogar auf 50 % bzw. 20–30 %. Die inneren Planeten überleben beim klassischen Modell nur in etwa 1 % der Fälle – beim um einem Planeten erweiterten Modell steigt die Wahrscheinlichkeit jedoch auf etwa 10 %.
Die Untersuchung zeigt jedoch auch, dass das Kriterium C bei beiden Modellen nur sehr selten erfüllt ist. Da das Modell auch die irregulären Monde Jupiters nicht beschreiben kann, ist es fragwürdig, ob es zur Erklärung irregulärer Monde herangezogen werden kann.
Literatur
- K. Tsiganis, R. Gomes, A. Morbidelli, H. F. Levison: Origin of the orbital architecture of the giant planets of the Solar System. In: Nature. Band 435, Nr. 7041, 26. Mai 2005, S. 459–461, doi:10.1038/nature03539 (englisch, oca.eu [PDF]).
- A. Morbidelli, H. F. Levison, K. Tsiganis, R. Gomes: Chaotic capture of Jupiter’s Trojan asteroids in the early Solar System. In: Nature. Band 435, Nr. 7041, 26. Mai 2005, S. 462–465, doi:10.1038/nature03540 (englisch, oca.eu [PDF]).
- R. Gomes, H. F. Levison, K. Tsiganis, A. Morbidelli: Origin of the cataclysmic Late Heavy Bombardment period of the terrestrial planets. In: Nature. Band 435, Nr. 7041, 26. Mai 2005, S. 466–469, doi:10.1038/nature03676 (englisch).
- Aurélien Crida: Solar System formation. In: Earth and Planetary Astrophysics (astro-ph.EP). 17. März 2009, arxiv:0903.3008v1 (englisch).
- David Nesvorny: Young Solar System’s Fifth Giant Planet? In: Earth and Planetary Astrophysics (astro-ph.EP). 13. September 2011, arxiv:1109.2949 (englisch).
Weblinks
Einzelnachweise
- K. Tsiganis, R. Gomes, A. Morbidelli, H. F. Levison: Origin of the orbital architecture of the giant planets of the Solar System. In: Nature. Band 435, Nr. 7041, 26. Mai 2005, ISSN 0028-0836, S. 459–461, doi:10.1038/nature03539 (nature.com).
- Franklin et al., Minor planets and comets in libration about the 2:1 resonance with Jupiter