Molekulare Modellierung
Unter molekularer Modellierung (amerikanisches Englisch: molecular modeling, britisches Englisch: molecular modelling) werden Techniken für computerunterstütztes Modellieren chemischer Moleküle zusammengefasst. Das Design von neuen Molekülen und deren Modellierung ist ein Teilgebiet der molekularen Modellierung (englisch computer-aided molecular design, CAMD).
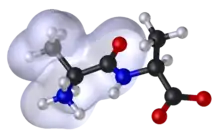
Beschreibung
Diese Techniken ermöglichen neben der räumlichen Darstellung von einfachsten bis zu hochkomplexen Molekülen auch die Berechnung ihrer physikochemischen Eigenschaften. Besonders in der medizinischen Chemie liegt die Anwendung darin, Strukturen für neue Wirkstoffe zu optimieren (Homologiemodelling). In diesem Bereich erfährt die molekulare Modellierung zunehmend eine Ergänzung durch die kombinatorische Chemie (Virtual Screening, QSAR, CoMFA, CoMSIA).
Mechanistische (semiempirische) und statistische Ansätze (Moleküldynamik, Monte-Carlo-Simulation) eignen sich eher für sehr große Moleküle oder Wechselwirkungen zwischen einer großen Anzahl an Molekülen, quantenchemische Berechnungsverfahren sind hingegen weitaus präziser, aber wegen des höheren Rechenaufwandes nur bei Molekülen kleiner und mittlerer Größe erste Wahl. Von der stetig wachsenden Rechenleistung moderner Computer profitiert die molekulare Modellierung.
Programme
Potentialhyperfläche
Die Potentialhyperfläche (PES) ist eine Darstellung, in der die potentielle Energie und die Struktur eines Moleküls einen mehrdimensionalen Raum aufspannen. Die Energie eines Moleküls wird in Abhängigkeit seiner Kernkoordinaten dargestellt.[1]
Koordinatensysteme
In der molekularen Modellierung ist die Wahl eines geeigneten Koordinatensystems wichtig. Es wird generell zwischen globalen und lokalen Koordinatensystemen unterschieden. Unter die globalen Koordinatensysteme fallen z. B. die orthonormierten kartesischen Koordinaten und die Kristallkoordinaten. Im Unterschied zu kartesischen Koordinaten sind die Winkel in Kristallkoordinaten nicht gleich 90°. Die lokalen Koordinatensysteme sind immer bezogen auf bestimmte Atome oder die Beziehungen der Atome zueinander (z. B. Symmetrieeigenschaften), hier wäre u. a. die Z-Matrix oder die Normalkoordinaten der molekularen Schwingungen zu nennen.[2]
Optimierung
Die Optimierung ist nach Roland W. Kunz das Auffinden eines vorteilhaften Zustandes eines Systems, also die Suche nach einem lokalen Minimums in der Nähe eines gegebenen Startpunktes.[3] Generell wird der Begriff Optimierung für die Suche nach kritischen Punkten nahe der Ausgangsstruktur verwendet. Als kritische Punkte bezeichnet man Minima, Maxima und Sattelpunkte der Potentialhyperfläche.[1]
Die meisten Optimierungsmethoden bestimmen den nächstgelegenen kritischen Punkt, eine multidimensionale Funktion kann allerdings sehr viele verschiedene kritische Punkte derselben Art enthalten.[4]
Optimierung allgemeiner Funktionen: Minima finden
Das Minimum mit dem niedrigsten Wert wird als globales Minimum bezeichnet, während alle anderen lokale Minima sind.[4]
Verfahren des steilsten Abstiegs / Gradientenmethoden
Das Verfahren des steilsten Abstiegs, auch Gradientenmethode genannt, nutzt die differenziellen Eigenschaften der Zielfunktion aus. Die Suchrichtung ist durch einen festgelegten negativen Gradienten (differentielle Eigenschaft der Hyperfläche) definiert. Die Optimierung erfolgt hier in die Richtung des negativen Gradienten, der die Richtung des steilsten Abstiegs von einem Ausgangswert angibt, bis keine Verbesserung mehr erzielt werden kann.[5]
Da die potentielle Energie als Funktion der Kernkoordinaten die PES bildet sind für die kritischen Punkte die Ableitungen der Kernkoordinaten-Funktionen besonders wichtig. Innerhalb der Gradientenmethode wird zwischen dem numerischen und dem analytischen Gradienten unterschieden. In der Praxis sollte nur mit Methoden gearbeitet werden, für die ein analytischer Gradient vorhanden ist.
Beim Durchlauf der Gradientenmethode werden keine Informationen aus vorhergegangenen Suchschritten verwendet.[4]
Methoden
Ein Hauptproblem der molekularen Modellierung ist nicht das Fehlen einer geeigneten Methode zur Berechnung der Moleküleigenschaften, sondern ein Zuviel an Methoden. Die Wahl der Methode für ein bestimmtes Problem sollte daher sorgfältig getroffen werden.
Methoden der Dichtefunktionaltheorie
Das Ziel der Dichtefunktionaltheorie ist ein geeignetes (Energie-)Funktional der Dichte zu finden. Die möglichen Funktionale sind auf drei Dimensionen, unabhängig von der Molekülgröße, beschränkt.
Die Leistung verschiedener Dichtefunktionaltheorie-Methoden (DFT) ähnelt den Hartree-Fock-Ergebnissen (HF) (siehe unten).[6]
B3LYP/6-31G*
Eine der am häufigsten verwendeten Verfahren zur Geometrieoptimierung ist B3LYP/6-31G*. Bei B3LYP (Kurzform für: Becke, 3-Parameter, Lee-Yang-Parr) handelt es sich um eine Approximationen zum Austausch-Korrelations-Energiefunktional in der Dichtefunktionaltheorie (DFT), B3LYP steht somit für die gewählte Methode. Die weitere Bezeichnung 6-31G bezieht sich auf den verwendeten Basissatz von John Pople. Die allgemeine Bezeichnung der Basissätze ist X-YZG. Hierbei steht das X für die Anzahl primitiver Gaussianer (primitiver Gauß-Funktionen), die jede Kernatomorbitalbasisfunktion umfassen. Y und Z zeigen an, dass die Valenzorbitale jeweils aus zwei Basisfunktionen zusammengesetzt sind. Die erste Basisfunktion besteht aus einer Linearkombination von Y primitiven Gaußfunktionen. Die zweite Basisfunktion besteht entsprechend aus einer Linearkombination von Z primitiven Gaußfunktionen. Die Verwendung von Linearkombinationen ist notwendig, da die primitiven Gaussianer in Kernnähe ein anderes Verhalten zeigen als Atomorbitale, durch die Linearkombination wird dieser Fehler minimiert. In diesem Fall impliziert das Vorhandensein von zwei Zahlen nach dem Bindestrich, dass dieser Basissatz ein Split-Valenz-Basissatz ist.[7][8]
Ein 6-31G-Basissatz beschreibt somit die inneren Orbitale als eine Linearkombination von sechs primitiven Gauß-Funktionen, die zu einer kontrahiert sind. Valenzorbitale werden entsprechend durch zwei kontrahierte Gaußfunktionen beschrieben. Eine der kontrahierten Gaußfunktionen ist eine Linearkombinationen von drei primitiven Gauß-Funktionen und die andere eine Linearkombination mit einer primitiven Gauß-Funktion.
Das Sternchen in 6-31G* weist auf eine Korrektur für die räumliche Abhängigkeit der Ladungsverteilung im Molekül hin. Dies geschieht durch sogenannte Polarisationsfunktionen.[9][8]
Methoden nach Hartree-Fock-Modellen
Im Unterschied zur Dichtefunktionaltheorie wird bei der Hartree-Fock-Approximation die Vielteilchenwellenfunktion durch eine Slater-Determinante der Einteilchenzustände (Produktzustände) ausgedrückt, dies führt dazu, dass das Pauli-Prinzip automatisch berücksichtigt wird. Ziel ist somit ein geeignetes (Energie-)Funktional der Wellenfunktion zu finden, diese Wellenfunktionen sind meist hochdimensional, was einen, im Vergleich zur DFT erhöhten Rechenaufwand zur Folge hat. Ein zu beachtender Fehler des Hartree-Fock-Produktansatzes ist die Annahme, dass die Gesamt-Wahrscheinlichkeitsdichte ein einfaches Produkt der Einzel-Wahrscheinlichkeitsdichten ist:
Dies ist eine physikalisch zweifelhafte Annahme, da Elektronen unkorreliert (also unabhängig voneinander) behandelt werden. Für eine genaue Betrachtung dürfen die Wechselwirkungen der Elektronen untereinander nicht vernachlässigt werden. Auch in der Form der Slater-Determinante werden die Elektronen unkorreliert behandelt.
Für die Geometrieoptimierung auf Hartree-Fock-Niveau werden u. a. häufig folgende Basissätze verwendet: STO-3G, 3-21G, 6-31G* bzw. 6-31G**, cc-pVDZ und cc-pVQZ.[10]
Basissätze
Die Wahl des verwendeten Basissatzes spielt ebenso wie die Wahl der Methode (HF, DFT …) eine wichtige Rolle in der molekularen Modellierung. Ein Basissatz beschreibt eine Reihe von Basisfunktionen, die die Gesamtelektronenwellenfunktion durch Linearkombination der Basisfunktionen annähert. Heute werden als Basisfunktionen fast ausschließlich primitive Gaußfunktionen verwendet, dies liegt vor allem an dem geringeren Rechenaufwand bei der Verwendung von Gauß-Funktionen im Vergleich zu anderen Basisfunktionen. Wenn andere Basisfunktionen verwendet werden sollen ist darauf zu achten, dass sie ein Verhalten aufweisen, das mit der Physik des Problems übereinstimmt; auch sollte die gewählte Basisfunktion schnell zu berechnen sein.[11]
Ein Basissatz heißt minimal, wenn er so viele Basisfunktionen enthält, dass alle Elektronen des Moleküls beschrieben werden können und nur ganze Sätze von Basisfunktionen vorkommen.
| Basissatz | Anzahl der Basisfunktionen |
|---|---|
| 3-21G | 13 |
| 6-31G* | 19 |
| cc-pVDZ | 24 |
| cc-pVQZ | 115 |
Die hier gezeigten Basissätze sind klein, eine typische DFT-Rechnung weist ca. 100.000 Basisfunktionen auf.
Weitere Begriffe in der molekularen Modellierung
- Eine adiabatische Reaktion ist eine molekulare Resektion, die auf derselben Born-Oppenheimer-Hyperfläche (BO-Hyperfläche) abläuft, sodass eine oder mehrere Trajektorien auf derselben BO-Hyperfläche liegen. Bei einer diabatischen Reaktion kommt es dagegen zum Wechsel der BO-Hyperfläche (z. B. vom Grundzustand des Moleküls in einen angeregten Zustand).[1]
- Generell sind diabatische Reaktionen nicht schwieriger zu berechnen als adiabatische, allerdings können open shell Systeme mit ungepaarten Elektronen zu einem vergrößerten Rechenaufwand führen.[1]
Literatur
- Roland W. Kunz: Molecular modelling für Anwender. Anwendung von Kraftfeld- und MO-Methoden in der organischen Chemie. 2. überarbeitete und erweiterte Auflage. Teubner, Stuttgart 1997, ISBN 3-519-13511-6 (Teubner-Studienbücher: Chemie).
Einzelnachweise
- Kunz, Roland W.: Molecular Modelling für Anwender: Anwendung von Kraftfeld- und MO-Methoden in der organischen Chemie. 1. Auflage. Teubner, Stuttgart 1991, ISBN 3-519-03511-1, S. 24–35.
- Kunz, Roland W.: Molecular Modelling für Anwender: Anwendung von Kraftfeld- und MO-Methoden in der organischen Chemie. 1. Auflage. Teubner, Stuttgart 1991, ISBN 3-519-03511-1, S. 35.
- Kunz, Roland W.: Molecular Modelling für Anwender: Anwendung von Kraftfeld- und MO-Methoden in der organischen Chemie. 1. Auflage. Teubner, Stuttgart 1991, ISBN 3-519-03511-1, S. 50.
- Jensen, Frank: Introduction to computational chemistry. 2. Auflage. John Wiley & Sons, Chichester, England 2007, ISBN 978-0-470-01186-7, S. 383–420.
- Kunz, Roland W.: Molecular Modelling für Anwender : Anwendung von Kraftfeld- und MO-Methoden in der organischen Chemie. 1. Auflage. Teubner, Stuttgart 1991, ISBN 3-519-03511-1, S. 56.
- Jensen, Frank: Introduction to computational chemistry. 2. Auflage. John Wiley & Sons, Chichester, England 2007, ISBN 978-0-470-01186-7, S. 369.
- Aron J. Cohen, Paula Mori-Sánchez, Weitao Yang: Challenges for Density Functional Theory. In: Chemical Reviews. Band 112, Nr. 1, 22. Dezember 2011, ISSN 0009-2665, S. 289–320, doi:10.1021/cr200107z.
- Basis Sets | Gaussian.com. Abgerufen am 4. Juli 2018 (amerikanisches Englisch).
- Warren J. Hehre: Ab initio molecular orbital theory. In: Accounts of Chemical Research. Band 9, Nr. 11, November 1976, ISSN 0001-4842, S. 399–406, doi:10.1021/ar50107a003.
- Jensen, Frank: Introduction to computational chemistry. 2. Auflage. John Wiley & Sons, Chichester, England 2007, ISBN 978-0-470-01186-7, S. 360.
- Jensen, Frank: Introduction to computational chemistry. 2. Auflage. John Wiley & Sons, Chichester, England 2007, ISBN 978-0-470-01186-7, S. 93 ff.