Mechanische Spektroskopie

Die Mechanische Spektroskopie ist eine Methode in der Materialwissenschaft, um das mechanische Materialverhalten in Abhängigkeit von der Zeit oder der Frequenz zu untersuchen. Der Begriff wurde 1990 von Leszek B. Magalas erstmals benutzt, um die anelastische Relaxation von Materialien zu beschreiben.[1]

Systematische Untersuchungen dieses Phänomens wurden aber schon seit den 1940er Jahren (z. B. durch Clarence Melvin Zener[2] oder Arthur S. Nowick und B. S. Berry)[3] durchgeführt.

Begriffsdefinition

Der Begriff Mechanische Spektroskopie hat sowohl makroskopische als auch mikroskopische Aspekte. Makroskopisch wird das zeitliche oder das frequenzabhängige Verhalten des "intakten" Materials bei ausschließlich elastischen Verhalten betrachtet.[4] Überwiegend ist das Verhalten linear (bzw. es wird der lineare Teil betrachtet), so dass als Grundlage die linearen Antworttheorie genutzt werden kann. Fragen zur Festigkeit sowie Plastizität und Bruch werden nicht beachtet. Das Ziel der Untersuchung ist die Funktion der zeitabhängigen Antwort eines Festkörpers (z. B. die Dehnung) auf eine zeitabhängige mechanische Belastung (z. B. eine Spannung). Diese Funktion ist von der Zeit, der Frequenz, der Temperatur oder Amplitude abhängig und wird als Spektrum bezeichnet. Daher der Name „Mechanische Spektroskopie“. Mikroskopisch wird der Einfluss der atomaren Bindungskräfte und Defekten (Punktfehler, Versetzungen usw.) betrachtet.

Anelastizität und Viskoelastizität

Ist ein Material Viskoelastisch, so gibt es zwischen Spannung und Dehnung einen eindeutigen Gleichgewichtszustand, der sich aber nicht sofort, sondern erst mit zeitlicher Verzögerung (asymptotisch) einstellt. Eine weitere Bedingung für Viskoelastizität ist der vollständige Rückgang der Verformung nach dem Entlasten. Ist dies nicht der Fall, so spricht man von Anelastizität.[5][6]

Funktionen und Spektren

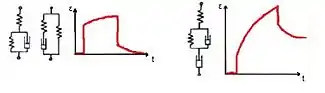
links: Typisches Dehnungsdiagramm einer anelastischen Relaxation mit zugehörigem Feder-Dämpfer-Diagramm.
rechts: Typisches Dehnungsdiagramm einer viskoelastischen Relaxation mit zugehörigem Feder-Dämpfer-Diagramm.

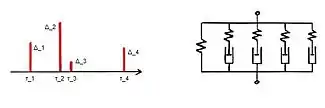
Ein diskretes Spektrum für Feder-Dämpfer-System eines Maxwell-Typs.

Um das anelastische Verhalten der Materialien zu beschreiben, kann man Antwortfunktionen oder Relaxationsspektren benutzen. Insbesondere für die Auswertung der Relaxationszeit und der Relaxationsstärke eignen sich Spektren besser, da hier in den rein elastischen Anteil und in den anelastischen Anteil unterschieden wird. Bei den Antwortfunktionen müssten diese Anteile mühsam herausgerechnet werden. Die anelastische Relaxation beruht oftmals auf der thermischen Aktivierung.[7] Daher kann die Materialdämpfung auch als Funktion der Temperatur dargestellt werden:

Q^{-1}={\frac {\Delta }{2}}\operatorname {sech} \ {\frac {Q_{a}}{k_{\mathrm {B} }}}\left({\frac {1}{T}}-{\frac {1}{T_{\mathrm {P} }}}\right)

$Q^{-1}$ : Dämpfung des Werkstoffes
$\Delta$ : Relaxationsstärke
$Q_{a}$ : „Aktivierungsenergie“
$k_{\mathrm {B} }$ : Boltzmann-Konstante
$T_{\mathrm {P} }$ : Temperatur im Peak

Als Gegenpol zur anelastischen Relaxation ist die statische Hysterese zu nennen.

Debye-Peak

Die Lösung für den Idealfall (den anelastischen Standardkörper) erhält man am besten mit dem Ansatz:

\varepsilon =\varepsilon _{0}e^{i\omega t}

;

\sigma =(\sigma '+\sigma '')e^{i\omega t}=(M'+iM'')\varepsilon

$M(\omega )$ : Modul des Werkstoffes
$Q^{-1}=\tan {\phi }$ : Verlustfaktor bzw. Materialdämpfung

In diesem Fall liegt das Relaxationsmaximum ${\frac {\Delta }{2}}$ bei $\omega \tau =1$ . Dieses Maximum wird als Debye-Peak bezeichnet.

Wichtige Typen von Relaxationsspektren

0D-Effekte

Die anelastische Relaxation über Punktdefekte ist thermisch aktiviert und kann nur durch Umgruppierung von Symmetriedefekten verursacht werden, wenn deren Symmetrie niedriger als die des Kristallgitters ist.

Zener-Relaxation

Die Zener-Relaxation wird durch die Ausrichtung von substitutellen Gitteratompaaren in Spannungsrichtung oder senkrecht dazu verursacht.

Gorsky-Relaxation

Der Gorsky-Effekt entsteht durch dehnungsinduzierte Bewegung von Atomen inhomogen verformten Objekten. Kommt es z. B. zu einer Biegung in Festkörpern, wandern einige Atome zu den Stellen, an denen der Atomabstand größer wird. Dabei entsteht ein Diffusionsstrom. Mit der Gorsky-Relaxation lässt sich aber der Diffusionskoeffizient von schnell diffundierenden Zwischengitteratomen einfach messen, wie z. B. von Wasserstoffatomen.

Snoek-Relaxation

Während bei der Gorsky-Relaxation durch die Volumenaufweitung entsteht, sind bei der Snoek-Relaxation die Umorientierung von elastische Dipole die Ursache.

Der Snoek-Effekt entsteht also durch spannungsinduzierte Bewegung von Atomen inhomogen verformten Objekten. Dies bewirkt eine Änderung des elastischen Feldes, die abhängig von der Temperatur und der Zeit ist.

Experimentelle Methoden

Ein DMA-Messgerät, womit auch die Vibrating-Reed-Methode durchgeführt werden kann. Die Probe (sample) wird zwischen die Greifer (grips) eingespannt. Dann wird eine Kammer (environmental chamber) darübergestülpt, um Messungen bei verschiedenen Temperaturen durchzuführen.

Insgesamt lassen sich die zahlreichen Untersuchungsmethoden in vier große Gruppen (eine statische und vier dynamische) einteilen, die auf der Zeit- bzw. Frequenzskala einen riesigen Bereich von mindestens 15 Zehnerpotenzen abdecken:

Methode	Elastische Messgröße	Anelastische Messgröße	Anwendung
Statisch Zugversuch	$E=\sigma /\varepsilon$	$\sigma$ zeitabhängig ( $\varepsilon =$ konstant) Spannungsrelaxation	Spannungsrelaxation, Kriechen
Subresonanz Erzwungene Schwingung Anregung: $\sigma =\sigma _{0}e^{i\omega t}$	Dehnungsamplitude $\varepsilon _{0}$	Verlustwinkel $\phi$	erzwungene Schwingungen
Resonanz	Resonanzfrequenz $f_{R}$	Dämpfung $Q^{-1}$	freie Schwingungen, stehende Welle
Ultraschall Puls-Echo-Methode	Schallgeschwindigkeit $c$	Schallschwächung $\alpha$	laufende Welle, Pulse

Während früher hauptsächlich Längs- und Torsionspendel bei den Experimenten eingesetzt wurden, hat sich heutzutage die Vibrating-Reed-Methode durchgesetzt. Hier wird meist die Temperatur kontinuierlich verändert und die Dämpfung sowie die Resonanzfrequenz der Probe gemessen.

Technische Anwendung

Die Mechanische Spektroskopie wird zur Entwicklung von Werkstoffen und Herstellung von Bauteilen mit gewünschten Dämpfungseigenschaften eingesetzt, z. B. besonders niedrige oder besonders hohe Dämpfung.

Eine andere Anwendungsmöglichkeit ist die Detektion von Wasserstoff in Metallen.

Siehe auch

Dynamisch-mechanische Analyse

Einzelnachweise

R. De Batist, L. B. Magalas: Mechanical Spectroscopy. In: R.W. Cahn, P. Haasen, E.J. Kramer (Hrsg.): Materials Science and Technology. Volume 2B: Characterization of Materials. VCH, Weinheim 1994, ISBN 3-527-28265-3.
C. Zener: Elasticity an Anelasticity in Metals. University of Chicago, Chicago 1948.
Arthur S. Nowick, B. S. Berry: Anelastic Relaxation in Crystalline Solids. Academic Press, New York 1972.
L. B. Magalas: Mechanical Spectroscopy – Fundamentals. In: Solid State Phenomena. 89, 2003, S. 1–22, doi:10.4028/www.scientific.net/SSP.89.1.
M. S. Blanter, H. Neuhäuser, I. S. Golovin, H.-R. Sinning: Internal Friction in Metallic Materials, A Handbook. Springer Series in Materials Science, Vol. 90, Springer, Berlin Heidelberg New York 2007, ISBN 978-3-540-68757-3.
R. Schaller, G. Fantozzi, G. Gremaud: Mechanical Spectroscopy Q^(-1). Trans Tech Publications, Uetikon, Zürich 2001.
Alexander Strahl: Anelastische Relaxationen durch Punktdefekte und Versetzungen in Fe-Al-Legierungen. 2006, urn:nbn:de:gbv:084-11370 (Dissertation, Technische Universität Carolo-Wilhelmina, Braunschweig).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] R. De Batist, L. B. Magalas: Mechanical Spectroscopy. In: R.W. Cahn, P. Haasen, E.J. Kramer (Hrsg.): Materials Science and Technology. Volume 2B: Characterization of Materials. VCH, Weinheim 1994, ISBN 3-527-28265-3.

[2] C. Zener: Elasticity an Anelasticity in Metals. University of Chicago, Chicago 1948.

[3] Arthur S. Nowick, B. S. Berry: Anelastic Relaxation in Crystalline Solids. Academic Press, New York 1972.

[4] L. B. Magalas: Mechanical Spectroscopy – Fundamentals. In: Solid State Phenomena. 89, 2003, S. 1–22, doi:10.4028/www.scientific.net/SSP.89.1.

[5] M. S. Blanter, H. Neuhäuser, I. S. Golovin, H.-R. Sinning: Internal Friction in Metallic Materials, A Handbook. Springer Series in Materials Science, Vol. 90, Springer, Berlin Heidelberg New York 2007, ISBN 978-3-540-68757-3.

[6] R. Schaller, G. Fantozzi, G. Gremaud: Mechanical Spectroscopy Q^(-1). Trans Tech Publications, Uetikon, Zürich 2001.

[7] Alexander Strahl: Anelastische Relaxationen durch Punktdefekte und Versetzungen in Fe-Al-Legierungen. 2006, urn:nbn:de:gbv:084-11370 (Dissertation, Technische Universität Carolo-Wilhelmina, Braunschweig).