Mean Time Between Failures

Mean Time Between Failures (kurz MTBF) ist die englische Bezeichnung für die mittlere Betriebsdauer zwischen Ausfällen für reparierbare Einheiten. Unter „Betriebsdauer“ versteht man die Betriebszeit zwischen zwei aufeinanderfolgenden Ausfällen einer solchen Einheit.

Die Definition nach IEC 60050 (191) lautet: Der Erwartungswert der Betriebsdauer zwischen zwei aufeinanderfolgenden Ausfällen.

Für Einheiten, die nicht instand gesetzt werden (können), ist der Erwartungswert (Mittelwert) der Verteilung von Lebensdauern die mittlere Lebensdauer MTTF (englisch mean time to failure). Umgangssprachlich werden die Begriffe oft synonym verwendet (in diesem Fall hat sich das Backronym „mean time before failure“ eingebürgert).

Veranschaulichung

MTBF ist ein Maß für die Zuverlässigkeit von Einheiten (Baugruppen, Geräten oder Anlagen), die nach einem Ausfall (down) instand gesetzt (up) werden. Dieses Verhalten lässt sich anhand folgender Grafik verdeutlichen:

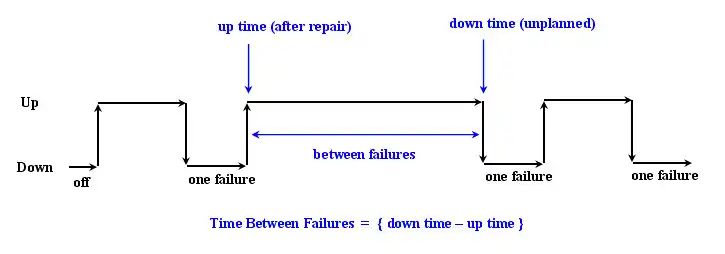
Der Betrieb der Einheit liegt zwischen dem Ereignis der Inbetriebnahme (up-time) und dem Ereignis des Ausfalls (down-time). Formal lässt sich die MTBF über einen langen Zeitraum, in welchem mit vielen Ausfällen und Inbetriebnahmen zu rechnen ist, ausdrücken als:

{\text{MTBF}}={\frac {\Sigma {({\text{start of downtime}}-{\text{start of uptime}})}}{\text{number of failures}}}.

Je höher der MTBF-Wert, desto zuverlässiger das Gerät. Ein Gerät mit einer MTBF von 100 Stunden wird im Mittel öfter ausfallen als ein gleichartiges Gerät mit einer MTBF von 1000 Stunden. Die mathematische Wahrscheinlichkeit, dass ein Gerät bei Nutzung innerhalb seiner regulären Gebrauchslebensdauer und Betriebsbedingungen die MTBF-Zeit ausfallfrei erreicht, beträgt 37 %.[1]

Werden MTBF-Angaben gemacht, so sollten zusätzlich die umgebungs- und funktionsbedingten Beanspruchungen, die Ausfallkriterien und die Geltungsdauer mit angegeben werden (z. B. Umgebungstemperatur, Anzahl der Start-/Stopp-Zyklen pro Tag, Einhaltung von Wartungsvorschriften etc.). Unter ungünstigen Betriebsbedingungen können wesentlich geringere MTBF-Werte (höhere Ausfallraten) als erwartet auftreten. Andererseits lässt sich durch ein Derating (und die durch diese Überdimensionierung kleineren Ausfallrate) die MTBF erhöhen.

Die MTBF muss unterschieden werden von der Brauchbarkeitsdauer (engl. useful life) eines Geräts: Letztere gibt die Zeitdauer an, auf die ein Gerät bei der Entwicklung ausgelegt wurde. Sie ist u. a. durch die Dimensionierung von Verschleißteilen bestimmt.

Berechnungsgrundlagen

Sowohl bei der mathematischen Ermittlung als auch der Anwendung von MTBF-Werten zur Zuverlässigkeitsprognose ist grundsätzlich vorauszusetzen, dass die betrachteten Einheiten während ihrer Gebrauchslebensdauer und unter vorgegebenen Betriebsbedingungen genutzt werden.[1] Man geht also davon aus, dass die betrachtete Einheit im mittleren Bereich der "Badewannenkurve", also mit konstanter Ausfallrate, betrieben wird. Dieser als Exponentialverteilung bezeichnete Zeitraum schließt Früh- und Abnutzungsausfälle aus.

Die MTBF wird berechnet als Erwartungswert der Ausfallzeit. Mit der Wahrscheinlichkeitsdichte $f(t)$ für einen Ausfall zur Zeit t gilt allgemein:

\mathrm {MTBF} =\int _{0}^{\infty }t\,f(t)\,dt\;.

Die MTBF lässt sich auch als Integral über die Zuverlässigkeitsfunktion $R(t)$ ausdrücken:

\mathrm {MTBF} =\int _{0}^{\infty }R(t)\,dt\;.

Um sich diesen Zusammenhang zu veranschaulichen, ist es zweckmäßig, die Zuverlässigkeitsfunktion in einem gedrehten Koordinatensystem zu betrachten: Auf der x-Achse von 0 bis 1 trage man eine große Zahl von Geräten sortiert nach deren Ausfallzeit ein, auf der y-Achse den Wert der Ausfallzeit. Die mittlere Ausfallzeit ist als Flächeninhalt unter der Kurve (Integral) abzulesen. Der Flächeninhalt unter der Kurve hat sich beim Drehen des Koordinatensystems natürlich nicht verändert, ist somit gleich dem Integral über $R(t)$ . Die beiden Integraldarstellungen der MTBF lassen sich mathematisch durch partielle Integration ineinander überführen.

Für den o. g. Fall des Betriebs einer Einheit im Zeitraum einer konstanter Ausfallrate λ gilt:

f(t)=\lambda \,e^{-\lambda t}

mit der Eulerschen Zahl e.

Somit ergibt sich die MTBF einer Einheit aus dem Kehrwert ihrer konstanten Ausfallrate:

\mathrm {MTBF} ={\frac {1}{\lambda }}.

Dieser Zusammenhang zwischen Ausfallabstand und Ausfallrate einer Einheit erlaubt eine einfache Ermittlung bzw. Umrechnung im o. g. Zeitraum der Gebrauchslebensdauer.

Ist die MTBF einer Einheit bekannt, so lässt sich eine wahrscheinlichkeitsbehaftete Aussage des Überlebens bis zu einem bestimmten Zeitpunkt angeben. Beispielsweise beträgt die Ausfallwahrscheinlichkeit eines Bauelements oder Gerätes bis zur MTBF 63,2 % (exakt 1-1/e).[1] Damit sind nach Erreichen der Zeit, die der MTBF entspricht, nur noch ungefähr 37 % der bei Testbeginn vorhandenen Einheiten funktionstüchtig und etwa 2/3 der Einheiten ausgefallen.[1] Diese Aussagen setzen voraus, dass die betrachtete Einheit im mittleren Bereich der "Badewannenkurve", also mit konstanter Ausfallrate, betrieben wird, es also keine systematischen Ausfälle gibt. Sie widerlegen auch die oft gemachte Annahme, dass es sich bei der MTBF um eine mittlere Lebensdauer (50 % Ausfälle) handelt.

Anwendungen

Der MTBF-Wert lässt sich als Kenngröße der Zuverlässigkeit von Bauelementen und Geräten oder zum Vergleich verschiedener Geräte oder Entwürfe verwenden. Dieser Wert ist jedoch nur bedingt als „mittlere Lebensdauer“ im Sinne eines Durchschnittswertes zu verstehen.

Schätzwerte für die MTBF können durch Lebensdauerversuche – fallweise auch mit erhöhten Beanspruchungen – ermittelt werden, in denen das Gerät z. B. Strahlung, Feuchtigkeit, Erschütterungen, Hitze und Ähnlichem ausgesetzt wird, z. B. durch einen Highly Accelerated Life Test. Die MTBF ist der Kehrwert der so ermittelten Ausfallrate der Baugruppe/Einheit. Diese Versuche sind nicht standardisiert, deshalb sind alle angegebenen MTBF-Werte nur innerhalb der Produktreihen eines Herstellers vergleichbar.

Abschätzung von Ausfallwahrscheinlichkeiten

Die MTBF kann zur Abschätzung von Ausfällen in Zeitintervallen verwendet werden. Beispielsweise sind bei Festplatten MTBF-Werte von 1.200.000 Stunden üblich (z. B. bei der WD RE3 500G), dies entspricht 137 Jahren. Aus dieser Zahl kann die Wahrscheinlichkeit p berechnet werden, dass es während der Nutzungsdauer zu einem Ausfall kommt:

p(T)=1-e^{-{\frac {T}{\mathrm {MTBF} }}}

Für $T=5a$ (Nutzungsdauer bei Festplatten oft 5 Jahre) gilt:

p(5a)=1-e^{-{\frac {5a}{137a}}}=3{,}6\,\%

Berechnung von MTBF aus Failure in Time

Bei dieser Anwendung zur Zuverlässigkeitsprognose lässt sich unter Kenntnis von MTTF-Werten abschätzen, ob gesetzte Zuverlässigkeitsziele erreicht werden können. Dazu sind genaue Kenntnisse des Aufbaus des Gerätes und der Ausfallraten der verwendeten Bauelemente notwendig (Ausfallraten oft angegeben in FIT: 1 FIT = 10⁻⁹/h). Die MTBF ist der Kehrwert der berechneten Ausfallrate der Baugruppe/Einheit, die sich wiederum aus der Summe der in Abhängigkeit von der Beanspruchung gewichteten Bauelementeausfallraten ergibt.

Bei der Berechnung der MTBF aus FIT muss berücksichtigt werden, dass FIT in der Regel ohne die Einheit „Ausfälle pro 10⁹ Stunden“ angegeben wird. Wird beispielsweise die MTBF eines reparierbaren Gerätes von einem Bauelement bestimmt, für das die FIT bekannt ist, dann ergibt sich die folgende Umrechnungsformel für die zu erwartende mittlere Zeit, die zwischen dem Ersatz dieses Bauelementes durch ein neues Bauelement verstreichen wird:

\mathrm {MTBF} ={\frac {10^{9}\,{\text{Stunden}}}{\mathrm {FIT} }}={\frac {114000\,{\text{Jahre}}}{\mathrm {FIT} }}

Beispiel: Für eine FIT von 1140 ergibt sich also MTBF = 100 Jahre.

Berechnung der Verfügbarkeit

Die MTBF wird auch zur Berechnung der „stationären“ Verfügbarkeit (engl. Availability) eingesetzt. Diese gibt an, wie groß die Wahrscheinlichkeit ist, dass ein System bei Anforderung den spezifizierten Dienst anbietet:

A={\frac {\mathrm {MTBF} }{\mathrm {MTBF} +\mathrm {MTTR} }}

mit der Wiederherstellungszeit MTTR.

Betriebswirtschaftlich wird die MTBF als Kennzahl zur Leistungsmessung (engl. Key Performance Indicator, KPI) herangezogen.

MTBF und Verfügbarkeit zusammengesetzter Systeme

Aus der Verfügbarkeit A oder der MTBF von Teilsystemen lässt sich die Gesamtverfügbarkeit eines Systems errechnen.

In allen Fällen wird davon ausgegangen, dass die Reparatur der Teilsysteme sofort nach dem Ausfall gestartet wird, insbesondere auch dann, wenn das Gesamtsystem aufgrund einer redundanten Auslegung noch funktioniert. Komplexere Systeme können aus Parallel- und Serienschaltungen zusammengesetzt sein und entsprechend berechnet werden.

Reihenschaltung

Ein System kann seriell aus zwei Teilsystemen a und b zusammengesetzt sein, d. h. beide Teilsysteme müssen verfügbar sein, damit das Gesamtsystem funktioniert. Für die Verfügbarkeit des Gesamtsystems gilt dann

A_{\text{seriell}}=A_{a}\cdot A_{b}

Nimmt man für die Teil- und Gesamtsysteme dieselbe mittlere Wiederherstellungszeit MTTR an, so erhält man für die Serienschaltung:

\mathrm {MTBF} _{\text{seriell}}={\frac {1}{{\frac {1}{\mathrm {MTBF} _{a}}}+{\frac {1}{\mathrm {MTBF} _{b}}}+{\frac {\mathrm {MTTR} }{\mathrm {MTBF} _{a}\cdot \mathrm {MTBF} _{b}}}}}

Parallelschaltung

Ist ein System parallel aus zwei funktionsgleichen redundanten Teilsystemen a und b aufgebaut, dann muss nur eines der Teilsysteme verfügbar sein, damit das Gesamtsystem arbeitet. Für die Verfügbarkeit des Gesamtsystems gilt:

A_{\text{parallel}}=1-(1-A_{a})\cdot (1-A_{b})

Nimmt man wiederum für Teil- und Gesamtsystem dieselbe mittlere Wiederherstellungszeit MTTR an, so erhält man für die Parallelschaltung:

\mathrm {MTBF} _{\text{parallel}}=\mathrm {MTBF} _{a}+\mathrm {MTBF} _{b}+{\frac {\mathrm {MTBF} _{a}\cdot \mathrm {MTBF} _{b}}{\mathrm {MTTR} }}

Normen

Für die Berechnung existieren Normen, beispielsweise

DIN EN/IEC 61709
SN 29500 der Siemens AG (wird laufend aktualisiert, neben elektronischen auch vermehrt elektromechanische Komponenten wie Relais, Schütze, Leistungsschalter, Überlastrelais, Zeitrelais usw. Befehls- und Meldegeräte, Drucktaster, Leuchtmelder, Positionsschalter sind in Arbeit)
SR-332 von Telcordia Technologies
MIL-HDBK-217 des US-Militärs (wird nicht mehr gepflegt)

Einzelnachweise

J. Lienig, H. Brümmer: Zuverlässigkeit elektronischer Geräte. In: Elektronische Gerätetechnik. Springer Vieweg, 2014, ISBN 978-3-642-40961-5, S. 55-58.

Literatur

Patrick Gehlen: Funktionale Sicherheit von Maschinen und Anlagen. Umsetzung der Europäischen Maschinenrichtlinie in der Praxis. 1. Auflage. Publicis Corporate Publishing, 2010, ISBN 978-3-89578-281-7.
Alessandro Birolini: Zuverlässigkeit von Geräten und Systemen. 1. Auflage. Springer, 1997, ISBN 3-540-60997-0.
Alessandro Birolini: Reliability Engineering: Theory and Practice. 7. Auflage. Springer, 2013, ISBN 978-3-642-39534-5.
Jens Lienig, Hans Brümmer: Elektronische Gerätetechnik. 1. Auflage. Springer, 2014, ISBN 978-3-642-40961-5.

Weblinks

Genauere Erklärung zur MTBF (englisch, pcguide.com)
noch eine Erklärung zu MTBF (englisch, storagereview.com)
Ausführliche Darstellung zur MTBF am Beispiel von Festplatten (englisch)
"MTBF" & "MTTR" kurz erklärt, edinn
Kurz erklärt: Festplatten-Lebensdauer, iX
BQR Care MTBF Kommerzielle MTBF Software

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[exponentialverteilung-1] J. Lienig, H. Brümmer: Zuverlässigkeit elektronischer Geräte. In: Elektronische Gerätetechnik. Springer Vieweg, 2014, ISBN 978-3-642-40961-5, S. 55-58.