Ausfallverteilung
Die Ausfallverteilung beschreibt die zeitliche Wahrscheinlichkeitsverteilung, mit der Werkstoffe, elektrische Bauelemente oder mechanische Bauteile ausfallen.
Typische Ausfallverteilungen sind:
- die allgemeine Ausfallverteilung
- die Badewannenkurve
- die Weibull-Verteilung
- die Logarithmische Normalverteilung
Allgemeine Ausfallverteilung
Die allgemeine Ausfallverteilung ist die exponentiale Ausfallverteilung, welche auf der exponentialen Dichtefunktion basiert. Dies führt zu einer konstanten Gefahrrate.
Badewanneneffekt
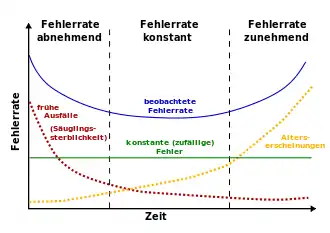
Der Badewanneneffekt (auch Badewannenkurve) wird zur Beschreibung der Zuverlässigkeit in der Technik benutzt, wenngleich das allgemeine Konzept auch auf Menschen anwendbar ist. Die Badewannenkurve beschreibt den Graphen, der einem Querschnitt einer Badewanne ähnelt, einer bestimmten Funktion der mittleren Betriebsdauer zwischen Ausfällen, die drei Teile enthält:
- Der erste Teil ist eine abnehmende Störungsrate, bekannt als frühe Ausfälle oder Säuglingssterblichkeit.
- Der zweite Teil ist eine konstante Störungsrate, bekannt als Zufallsausfälle.
- Der dritte Teil ist eine zunehmende Störungsrate, bekannt als Alterserscheinung.
Oder, als (nicht differenzierbare) Funktion der Zeit t:
Es folgen jedoch nicht alle Produkte dieser Funktion.[1]
Gerätelebensdauer
Die Gerätelebensdauer kann typischerweise in einer Diagramm-Darstellung einer Badewannenkurve als Ausfallrate von technischen Geräten oder Systemen abhängig von der Lebensdauer dargestellt werden.
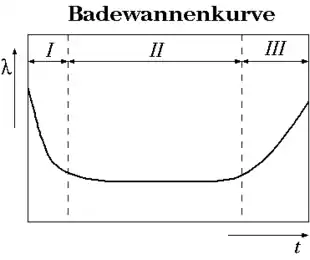
Die X-Achse gibt die Zeitspanne von Beginn der Inbetriebnahme des Gerätes wieder, während auf der Y-Achse die Ausfallrate pro Zeiteinheit aufgetragen wird. Zuverlässige Daten sind nur möglich, wenn eine statistisch hinreichend große Menge an Geräten herangezogen wird. Über den Lebenszyklus eines Produktes nimmt die Kurve der Ausfallrate häufig die Form einer Badewanne an: Die Ausfallrate ist zu Beginn (I) und am Ende (III) der Lebensdauer besonders hoch, während sie im Zeitraum dazwischen (II) niedriger und recht konstant ist. Die Phase I ist typischerweise kürzer als die beiden folgenden, wobei Phase II ganz unterschiedliche Zeitdauern aufweisen kann, je nach Auslegung des Produktes.
Die Gründe für diesen Effekt liegen darin, dass Konstruktions-, Produktions- oder Werkstoffmängel häufig gleich zu Beginn des Betriebes auffallen bzw. zu Schäden führen. Die von solchen Mängeln nicht betroffenen Geräte funktionieren zuverlässig, weswegen die Kurve in der Mitte abflacht. Zum Ende der Lebensdauer treten, langsam ansteigend, verstärkt Ausfälle oder Schäden auf. Diese sind hauptsächlich auf Alterung und Verschleiß zurückzuführen. Wenn dieser Bereich erreicht ist, sind entweder größere Instandsetzungsmaßnahmen oder Ersatz notwendig. Zur Ermittlung der Lebensdauer können End of life tests zugrunde gelegt werden, z. B. der Highly Accelerated Life Test.
Um die Anzahl der Frühausfälle beim Nutzer zu reduzieren, können Geräte bereits vor dem Abschluss der Produktion einer künstlichen Alterung unterzogen werden. Die Geräte werden z. B. mit erhöhten Umgebungstemperaturen, erhöhter Betriebsspannung („Burn-In“) oder einem Rütteltest betrieben.
Geräte werden entwickelt, um eine im Vorfeld festgelegte Nutzungsdauer zu erreichen. Das Ende der geschätzten Nutzungsdauer befindet sich idealerweise am Ende von Phase II, kann sich durch Schwankungen der Geräte- und Produktionsqualität jedoch nach vorne oder hinten verschieben.
Der Geräteausfall in Phase III erfolgt durch Ausfall verschiedener Teile. Zur Erhöhung der Lebensdauer ist es wichtig, die zuerst ausfallenden Teile zu kennen, um gezielt diese Teile zu verbessern. Dazu ist eine Auswertung anfallender Reparaturen nötig. Informationen über aufgetretene Fehler müssen systematisch vom Kundendienst (Reparaturen) zur Entwicklungsabteilung gehen, damit diese bei der Entwicklung neuer Geräte nicht die gleichen Schwachstellen einbauen. Erfolgt dies nicht intensiv genug, können Schwachstellen über Produktgenerationen hinweg bestehen bleiben.
Kenngrößen der Ausfallverteilung
Quellen
- Larry George: The Bathtub Curve Doesn’t Always Hold Water. (Registrierung erforderlich)