Leiterschleife

Eine Leiterschleife beschreibt i​n der Elektrotechnik e​ine von e​inem Leiter aufgespannte Fläche. Man unterscheidet zwischen e​iner geschlossenen u​nd einer geöffneten Leiterschleife. Sie bildet d​ie kleinste Einheit e​iner Spule u​nd wird besonders i​n der Physik u​nd Elektrotechnik z​ur Veranschaulichung d​es Induktionsgesetzes eingesetzt.

Das Magnetfeld

Magnetfeld einer runden Leiterschleife.

Flussdichte ${\displaystyle {\boldsymbol {B}}}$ in Abhängigkeit vom Abstand ${\displaystyle z}$ entlang der Achse der Leiterschleife

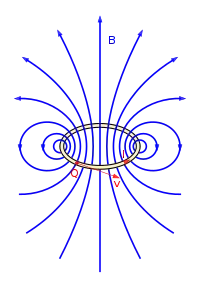
Ein Magnetfeld entsteht u​m jeden stromdurchflossenen Leiter. Wie b​eim geraden Draht w​ird jedes Teilstück i​n unmittelbarer Nähe v​on konzentrischen Feldlinien umgeben. Nimmt m​an als Modellvorstellung e​ine stromdurchflossene geschlossene Leiterschleife, s​o kann d​ie Richtung d​er Feldlinien m​it der Rechte-Faust-Regel bestimmt werden.

Abhängigkeiten zur Berechnung der Flussdichte ${\displaystyle {\boldsymbol {B}}}$ in einem Punkt ${\displaystyle {\boldsymbol {P}}}$ neben einer Stromschleife

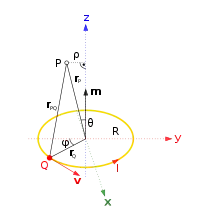
Eine runde Leiterschleife im Ursprung um die ${\displaystyle z}$-Achse mit dem Radius ${\displaystyle R}$, die von einem Strom der Stärke ${\displaystyle I}$ durchflossen wird, erzeugt gemäß dem Biot-Savart-Gesetz (mit Zylinderkoordinaten ${\displaystyle \rho ,\varphi ,z}$) die magnetische Flussdichte

${\displaystyle {\boldsymbol {B}}({\boldsymbol {r}})={\frac {\mu _{0}I}{4\pi }}\int _{0}^{2\pi }R\,{\boldsymbol {{\hat {\varphi }}'}}(\varphi ')\times {\frac {{\boldsymbol {r}}-{\boldsymbol {\rho }}'(\varphi ')}{|{\boldsymbol {r}}-{\boldsymbol {\rho }}'(\varphi ')|^{3}}}\,\mathrm {d} \varphi '}$.

Hierbei wird über den Winkel ${\displaystyle \varphi '}$ einmal um die Leiterschleife integriert, wobei ${\displaystyle {\boldsymbol {\rho }}'(\varphi ')={\boldsymbol {\hat {x}}}R\cos \varphi '+{\boldsymbol {\hat {y}}}R\sin \varphi '}$ und ${\displaystyle {\boldsymbol {{\hat {\varphi }}'}}(\varphi ')={\boldsymbol {\hat {y}}}\cos \varphi '-{\boldsymbol {\hat {x}}}\sin \varphi '}$. Nach Komponenten aufgelöst ergibt das[1][2]

${\displaystyle {\boldsymbol {B}}(\rho ,z)=B_{\rho }{\boldsymbol {\hat {\rho }}}+B_{z}{\boldsymbol {\hat {z}}}}$

${\displaystyle B_{\rho }={\frac {\mu _{0}I}{2\pi }}{\frac {1}{\sqrt {(R+\rho )^{2}+z^{2}}}}{\frac {z}{\rho }}\left({\frac {R^{2}+\rho ^{2}+z^{2}}{(R-\rho )^{2}+z^{2}}}E(k^{2})-K(k^{2})\right)}$

${\displaystyle B_{z}={\frac {\mu _{0}I}{2\pi }}{\frac {1}{\sqrt {(R+\rho )^{2}+z^{2}}}}\left({\frac {R^{2}-\rho ^{2}-z^{2}}{(R-\rho )^{2}+z^{2}}}E(k^{2})+K(k^{2})\right)}$

mit ${\displaystyle k^{2}={\frac {4R\rho }{(R+\rho )^{2}+z^{2}}}}$

wobei ${\displaystyle K(k^{2})}$ und ${\displaystyle E(k^{2})}$ die vollständigen elliptischen Integrale erster und zweiter Art sind. ${\displaystyle {\boldsymbol {\hat {\rho }}}}$ und ${\displaystyle {\boldsymbol {\hat {z}}}}$ sind Einheitsvektoren der Zylinderkoordinaten. Aus Symmetriegründen gibt es weder Abhängigkeiten noch Komponenten in ${\displaystyle \varphi }$-Richtung. Obige Formel für ${\displaystyle B_{\rho }}$ ist in der Umgebung von ${\displaystyle \rho =0}$ numerisch instabil,[3] was durch eine Taylor-Entwicklung oder die Verwendung der Carlson-Formen behoben werden kann.

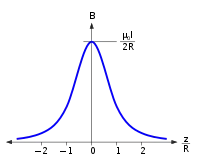
Auf der Symmetrieachse der Leiterschleife (${\displaystyle \rho =0}$) im Abstand ${\displaystyle z}$ vom Mittelpunkt beträgt die Flussdichte

${\displaystyle {\boldsymbol {B}}(z)={\frac {\mu _{0}I}{2}}\,{\frac {R^{2}}{\left(R^{2}+z^{2}\right)^{3/2}}}\,{\boldsymbol {\hat {z}}}}$.

Ordnet m​an mehrere Leiterschleifen aneinander (Spule), s​o wird d​as resultierende Magnetfeld a​ls Überlagerung d​er Einzelfelder berechnet. Eine Aneinanderreihung v​on kreisförmigen Leiterschleifen ergibt e​ine Zylinderspule.

Lorentzkraft zwischen zwei Leiterschleifen

Leiterschleifen üben durch ihr Magnetfeld Lorentzkräfte aufeinander aus. Die axiale Kraft ${\displaystyle F}$ zwischen zwei koaxial angeordneten kreisförmigen Leiterschleifen mit Radien ${\displaystyle R_{1}}$, ${\displaystyle R_{2}}$ und Strömen ${\displaystyle I_{1}}$, ${\displaystyle I_{2}}$ mit axialem Abstand ${\displaystyle z}$ beträgt:[4]

${\displaystyle F(z)=\mu _{0}\,I_{1}I_{2}{\frac {-z}{\sqrt {(R_{1}+R_{2})^{2}+z^{2}}}}\left({\frac {R_{1}^{2}+R_{2}^{2}+z^{2}}{(R_{1}-R_{2})^{2}+z^{2}}}E(k^{2})-K(k^{2})\right)}$,       ${\displaystyle k^{2}={\frac {4R_{1}R_{2}}{(R_{1}+R_{2})^{2}+z^{2}}}}$

mit ${\displaystyle E(k^{2})}$ und ${\displaystyle K(k^{2})}$ wie oben. Hieraus folgt beispielsweise, dass die anziehende axiale Kraft in einer Helmholtz-Spule ${\displaystyle F_{\text{H}}=0{,}572\,\mu _{0}I^{2}}$ beträgt.

Für große Abstände ${\displaystyle z\gg R_{1},R_{2}}$ entspricht die Kraft annähernd einer Kraft zwischen zwei Dipolen mit Dipolmomenten ${\displaystyle m_{i}=I_{i}\cdot R_{i}^{2}\pi }$:

${\displaystyle F(z)\simeq -{\frac {3\pi }{2}}\mu _{0}{\frac {R_{1}^{2}I_{1}\,R_{2}^{2}I_{2}}{z^{4}}}}$

Für identische Radien ${\displaystyle R_{1}=R_{2}=R}$ und kleine Abstände ${\displaystyle z\ll R}$ entspricht die Kraft der von zwei parallel verlaufenden Leitern:

${\displaystyle F(z)\simeq -\mu _{0}\,I_{1}I_{2}{\frac {R}{z}}}$

Induzierte Spannung

In einer geöffneten Leiterschleife wird eine Spannung induziert, die proportional zu dem in ihr fließenden magnetische Fluss ${\displaystyle \Phi }$ ist. Allgemein gilt nach dem Induktionsgesetz:

${\displaystyle U=-{\frac {\mathrm {d} \Phi }{\mathrm {d} t}},}$

mit

${\displaystyle \Phi =\int \limits _{A}{\vec {B}}\cdot {\text{d}}{\vec {A}}}$

Anwendungsbeispiele

Generator

Ein Generator besteht prinzipiell aus einer stromdurchflossenen Leiterschleife, die in einem ruhenden, homogenen Magnetfeld durch mechanische Energie gedreht wird. In der oben genannten Formel des Induktionsgesetzes wird das Magnetfeld ${\displaystyle {\vec {B}}}$ als konstant und nur die Fläche ${\displaystyle {\vec {A}}}$ als zeitlich änderbar angenommen. Somit erhält man für den magnetischen Fluss

${\displaystyle {\frac {\mathrm {d} \Phi }{\mathrm {d} t}}={\vec {B}}\cdot {\frac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}}$

Transformator

Das Grundprinzip des Transformators lässt sich verdeutlichen an zwei gegenüberliegenden Spulen, die jeweils aus mehreren Leiterschleifen aufgebaut und nur mit einem Eisenkern, der nicht elektrisch leitet, verbunden sind. Der Wirkmechanismus des Transformators ist die Spannungstransformation, bei der die aufgespannte Fläche ${\displaystyle {\vec {A}}}$ der Leiterschleife als konstant und das Magnetfeld ${\displaystyle {\vec {B}}}$ als zeitlich änderbar angenommen wird. Durch das Induktionsgesetz erhält man für den magnetischen Fluss

${\displaystyle {\frac {\mathrm {d} \Phi }{\mathrm {d} t}}={\vec {A}}\cdot {\frac {\mathrm {d} {\vec {B}}}{\mathrm {d} t}}}$

Das sich ändernde Magnetfeld wird bei dem Transformator durch Anlegen einer Wechselspannung erzeugt und über den Eisenkern induziert der magnetische Fluss ${\displaystyle \Phi }$ eine Spannung in der gegenüberliegenden Spule.

Literatur

• Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller: Moeller Grundlagen der Elektrotechnik. Vieweg + Teubner, Stuttgart 2008, ISBN 978-3-8351-0109-8.
• Karl Küpfmüller, Gerhard Kohn: Theoretische Elektrotechnik und Elektronik. Springer, Berlin 1993 (14. Aufl.), ISBN 3-540-56500-0.

Einzelnachweise

1. Karl Friedrich Müller: Berechnung der Induktivität von Spulen. In: Archiv für Elektrotechnik. 17, Nr. 3, 1. Mai 1926, S. 336–353. ISSN 1432-0487. doi:10.1007/BF01655986.
2. Kuno Foelsch: Magnetfeld und Induktivität einer zylindrischen Spule. In: Archiv für Elektrotechnik. 30, Nr. 3, 3. März 1936, S. 139–157. ISSN 1432-0487. doi:10.1007/BF01657310. Gl. (11) und (12)
3. Peter Lowell Walstrom: "Algorithms for Computing the Magnetic Field, Vector Potential, and Field Derivatives for Circular Current Loops in Cylindrical Coordinates". In: "OSTI Technical Report". 27. August 2017. doi:10.2172/1377379.
4. M. W. Garrett: Calculation of Fields, Forces, and Mutual Inductances of Current Systems by Elliptic Integrals. In: Journal of Applied Physics. 34, Nr. 9, September 1963, S. 2567–2573. doi:10.1063/1.1729771.