Napoleon-Punkt

Die beiden Napoleon-Punkte, benannt nach dem französischen Feldherrn und Kaiser Napoléon Bonaparte, gehören zu den ausgezeichneten Punkten im Dreieck.

Der 1. Napoleon-Punkt ist folgendermaßen definiert:

Über den Seiten eines gegebenen Dreiecks werden nach außen drei gleichseitige Dreiecke gezeichnet. Verbindet man die Schwerpunkte dieser Dreiecke mit den gegenüberliegenden Ecken des ursprünglichen Dreiecks, so schneiden sich die Verbindungsgeraden in einem Punkt, dem 1. Napoleon-Punkt des gegebenen Dreiecks.

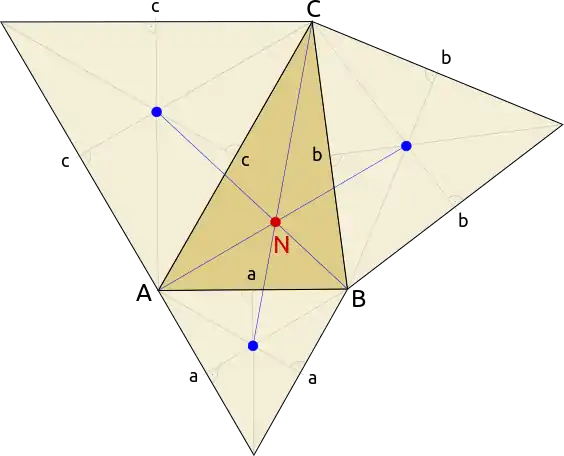
Zeichnet man die gleichseitigen Dreiecke jeweils auf die andere Seite, so erhält man entsprechend den 2. Napoleon-Punkt.

Die Verbindungslinien der drei Schwerpunkte bilden immer ein gleichseitiges Dreieck, unabhängig von der Länge der Grundseiten der Aufsetzdreiecke. Dieses Dreieck hat den gleichen Schwerpunkt wie das ursprüngliche Dreieck ABC.

Eigenschaften

• Die beiden Napoleon-Punkte liegen auf der Kiepert-Hyperbel.

Koordinaten

Napoleon-Punkte (${\displaystyle X_{17}}$ und ${\displaystyle X_{18}}$)
Trilineare Koordinaten	${\displaystyle \csc \left(\alpha \pm {\frac {\pi }{6}}\right)\,:\,\csc \left(\beta \pm {\frac {\pi }{6}}\right)\,:\,\csc \left(\gamma \pm {\frac {\pi }{6}}\right)}$
Baryzentrische Koordinaten	${\displaystyle a\cdot \csc \left(\alpha \pm {\frac {\pi }{6}}\right)\,:\,b\cdot \csc \left(\beta \pm {\frac {\pi }{6}}\right)\,:\,c\cdot \csc \left(\gamma \pm {\frac {\pi }{6}}\right)}$

Siehe auch

Ausgezeichnete Punkte im Dreieck, Napoleon-Dreieck

Weblinks

• Eric W. Weisstein: Napoleon Points. In: MathWorld (englisch).
• Napoleon-Punkt – eine Visualisierung des 1. Napoleon-Punktes mit dem dynamischen Geometrieprogramm GeoGebra