Vecten-Punkt

Die beiden Vecten-Punkte gehören z​u den besonderen Punkten e​ines Dreiecks. Sie g​ehen zurück a​uf den französischen Mathematiker Vecten (1811/1812) zurück.[1]

Erster Vecten-Punkt V₁ mit Kiepert-Dreieck ${\displaystyle {\mathcal {K}}_{\frac {\pi }{4}}}$ (rot)

Erster Vecten-Punkt

Über den Seiten eines Dreieck ABC werden nach außen drei Quadrate gezeichnet. Jeder der drei Quadratmittelpunkte, die das Kiepert-Dreieck ${\displaystyle {\mathcal {K}}_{\frac {\pi }{4}}}$ bilden, wird mit der gegenüberliegenden Ecke des ursprünglichen Dreiecks verbunden. Die Verbindungsgeraden schneiden sich in einem Punkt, der als erster Vecten-Punkt bezeichnet wird und die Kimberling-Nummer X(485) trägt.

Zweiter Vecten-Punkt

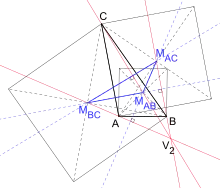
Zweiter Vecten-Punkt V₂

Zeichnet m​an die Quadrate n​ach innen s​tatt nach außen, s​o erhält m​an den zweiten Vecten-Punkt m​it Kimberling-Nummer X(486).

Eigenschaften

• Die beiden Vecten-Punkte liegen auf der Kiepert-Hyperbel.
• Die Vecten-Punkte liegen mit dem Mittelpunkt des Feuerbach-Kreises (Neun-Punkte-Kreises) auf einer Geraden.

Koordinaten

Vecten-Punkte (${\displaystyle X_{485}}$ und ${\displaystyle X_{486}}$)
Trilineare Koordinaten	${\displaystyle \sec \left(\alpha \pm {\frac {\pi }{4}}\right)\,:\,\sec \left(\beta \pm {\frac {\pi }{4}}\right)\,:\,\sec \left(\gamma \pm {\frac {\pi }{4}}\right)}$
Baryzentrische Koordinaten	${\displaystyle \sin \alpha \cdot \sec \left(\alpha \pm {\frac {\pi }{4}}\right)\,:\,\sin \beta \cdot \sec \left(\beta \pm {\frac {\pi }{4}}\right)\,:\,\sin \gamma \cdot \sec \left(\gamma \pm {\frac {\pi }{4}}\right)}$
Das Pluszeichen gilt für den ersten Vecten-Punkt, das Minuszeichen für den zweiten.

Literatur

• Sotirios E. Louridas, Michael Th. Rassias: Problem-Solving and Selected Topics in Euclidean Geometry: In the Spirit of the Mathematical Olympiads. Springer, 2014, ISBN 978-1-4614-7273-5, S. 62–63
• Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik: 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen. Springer, 2015, ISBN 978-3-662-45461-9, S. 4–7, 93

Weblinks

• Kimberling’s Encyclopedia of Triangle Centers (englisch)
• Eric W. Weisstein: Vecten Points. In: MathWorld (englisch).

Einzelnachweise

1. Über Vecten ist wenig überliefert. Bekannt ist, dass er von 1810 bis 1816 als „professeur de mathématiques spéciales“ am Lycée de Nîmes tätig war und 22 Beiträge in der von dem Mathematiker Joseph Gergonne herausgegebenen Zeitschrift Annales veröffentlichte. Siehe dazu: Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik: 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen. Springer, 2015, ISBN 978-3-662-45461-9, S. 4