Listenfärbung

Die Listenfärbung i​st ein Begriff d​er Graphentheorie u​nd eine Verallgemeinerung d​er Kantenfärbung u​nd der Knotenfärbung.

Definition

Ist ${\displaystyle G=(V,E)}$ ein Graph und ${\displaystyle (F_{v})_{v\in V}}$ eine Mengenfamilie beliebiger Mengen, so heißt eine gültige Knotenfärbung ${\displaystyle c:v\mapsto F_{v}}$ für alle Knoten des Graphen eine Färbung aus den Listen ${\displaystyle F_{v}}$ oder Listenfärbung. Ein Graph heißt k-listenfärbbar, wenn für alle Listen mit k Elementen stets eine Knotenfärbung aus diesen Listen existiert. Das kleinste k, so dass der Graph k-listenfärbbar ist, heißt listenchromatische Zahl des Graphen und wird mit ${\displaystyle ch(G)}$ bezeichnet.

Anschaulich w​ird also z​u jedem Knoten e​ine Liste m​it verfügbaren Farben vorgegeben u​nd der Graph m​uss daraufhin s​o gefärbt werden, d​ass zwei benachbarte Knoten n​ie dieselbe Farbe haben.

Analog lassen sich Kantenfärbungen aus Listen definieren. Das kleinste k, so dass G für alle Listen mit je k Farben kantenfärbbar ist, wird listenchromatischer Index genannt und mit ${\displaystyle ch'(G)}$ bezeichnet. Formal ist ${\displaystyle ch'(G)=ch(L(G))}$, wobei ${\displaystyle L(G)}$ der Kantengraph von ${\displaystyle G}$ ist.

Beispiel

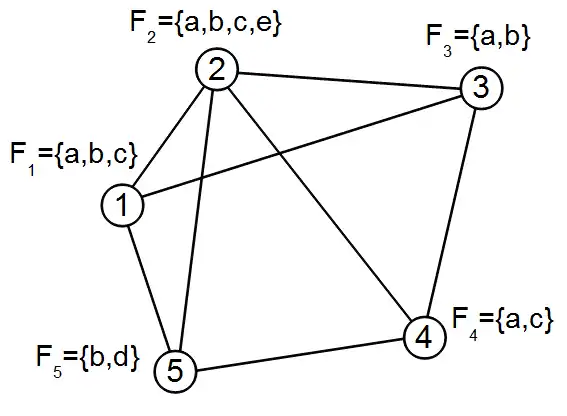
Für den oben Abgebildeten Graphen mit 5 Knoten ist zu jedem Knoten ${\displaystyle i}$ eine Liste ${\displaystyle F_{i}}$ von verfügbaren Farben für eine Knotenfärbung vorgegeben. Eine gültige Knotenfärbung aus den Listen wäre z. B. ${\displaystyle c(3)=c(5)=b\;,\;c(1)=c(4)=a\;,c(2)=e}$

Eigenschaften

• Da Listenfärbungen eine Verallgemeinerung von gewöhnlichen Färbungen sind, gilt stets ${\displaystyle ch(G)\geq \chi (G)}$ und ${\displaystyle ch'(G)\geq \chi '(G)}$. Dabei ist ${\displaystyle \chi (G)}$ die Chromatische Zahl des Graphen ist und ${\displaystyle \chi '(G)}$ die Kantenchromatische Zahl.
• Sind alle Listen ${\displaystyle F_{v}}$ gleich, so entspricht die Listenfärbung genau der Kantenfärbung bzw. Knotenfärbung.
• Jeder planare Graph ist 5-Listenfärbbar.
• Für jeden bipartiten Graph gilt ${\displaystyle ch'(G)=\chi '(G)=\Delta (G)}$ wobei ${\displaystyle \Delta (G)}$ der Maximalgrad des Graphen ist.
• Vermutlich gilt für jeden Graphen ${\displaystyle ch'(G)=\chi '(G)}$ (Listenfärbungsvermutung). Dies wurde aber bisher nicht bewiesen.

Literatur

• Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (354 Seiten, Online-Version).