Irreduzible Matrix

Irreduzibilität v​on Matrizen i​st ein Konzept d​er linearen Algebra, welches e​nge Verbindungen z​ur Graphentheorie aufweist. Vereinfacht gesagt i​st eine Matrix irreduzibel, w​enn ihre Zeilen u​nd Spalten n​icht so permutiert werden können, d​ass die Matrix i​n die untere Blockdreiecksgestalt überführt wird.

Neben Anwendungen i​n der Graphentheorie, findet d​as Konzept d​er Irreduzibilität Anwendung i​n der Theorie d​er positiven Eigenwerte u​nd -vektoren, s​iehe etwa Satz v​on Perron-Frobenius.

Definition

Eine Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ heißt reduzibel, wenn eine Permutationsmatrix ${\displaystyle P}$ existiert, so dass

${\displaystyle PAP^{T}={\begin{pmatrix}A_{MM}&0\\A_{NM}&A_{NN}\end{pmatrix}}.}$

Dabei ist ${\displaystyle A_{MM}}$ aus ${\displaystyle \mathbb {R} ^{p\times p}}$ mit ${\displaystyle p\in \{1,\ldots ,n-1\}}$ und die anderen Blockmatrizen dementsprechend passend dimensioniert. Ist diese Umordnung nicht möglich, so heißt die Matrix irreduzibel.

Potenz und Irreduzibilität

Sind alle Einträge der Matrix ${\displaystyle A}$ nichtnegativ und ist die Hauptdiagonale echt positiv, dann ist die Irreduzibilität von ${\displaystyle A}$ äquivalent dazu, dass eine Zahl ${\displaystyle k\in \mathbb {N} }$ existiert, für die

${\displaystyle A^{k}>0}$

gilt, das heißt, dass alle Einträge der Matrixpotenz ${\displaystyle A^{k}}$ positiv sind.[1] Etwas schwächer ist die Aussage, dass eine Matrix ${\displaystyle A}$ irreduzibel ist, wenn ${\displaystyle A\geq 0}$ gilt und ein ${\displaystyle k\in \mathbb {N} }$ existiert, sodass ${\displaystyle A^{k}>0}$ ist.

Eine Matrix ${\displaystyle A}$ mit nichtnegativen Einträgen ist genau dann irreduzibel, wenn es zu jedem Indexpaar ${\displaystyle (i,j)}$ eine Zahl ${\displaystyle k\in \mathbb {N} }$ gibt, so dass der ${\displaystyle (i,j)}$-Eintrag von ${\displaystyle A^{k}}$ positiv ist.

Verwendung

Irreduzible Matrizen spielen eine Rolle für die Existenz von Eigenvektoren und die Dimension des dazugehörigen Eigenraums, siehe dazu Satz von Perron-Frobenius. Des Weiteren gibt es eine enge Verbindung zur Graphentheorie: Die Adjazenzmatrix eines gerichteten Graphen ist genau dann irreduzibel, wenn der Graph stark zusammenhängend ist. Des Weiteren gilt: ist ${\displaystyle A}$ irreduzibel, so ist auch ${\displaystyle A^{T}}$ irreduzibel. Außerdem ist die Irreduzibilität einer stochastischen Matrix äquivalent zur Irreduzibilität der Markow-Kette, welche durch die stochastische Matrix beschrieben wird.

Beispiel

Der Adjazenzgraph der Matrix ${\displaystyle A}$. Es existiert kein Pfad von Knoten 3 zu Knoten 2, der Graph ist also nicht stark zusammenhängend.

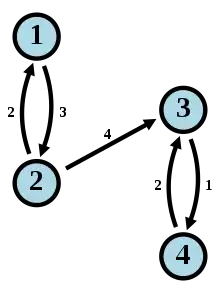
Betrachte a​ls Beispiel d​ie folgende Matrix:

${\displaystyle A={\begin{bmatrix}0&3&0&0\\2&0&4&0\\0&0&0&1\\0&0&2&0\\\end{bmatrix}}}$

Die transponierte Matrix i​st

${\displaystyle A^{T}={\begin{bmatrix}0&2&0&0\\3&0&0&0\\0&4&0&2\\0&0&1&0\\\end{bmatrix}}}$

Damit ist die Matrix ${\displaystyle A^{T}}$ in der geforderten Blockdreiecksform und ${\displaystyle A}$ deshalb reduzibel.

Weblinks

• Eric W. Weisstein: Reducible Matrix. In: MathWorld (englisch).

Literatur

• Peter Knabner, Wolf Barth: Lineare Algebra. Grundlagen und Anwendungen (= Springer-Lehrbuch). Springer Spektrum, Berlin u. a. 2013, ISBN 978-3-642-32185-6.

Einzelnachweise

1. Peter Knabner, Wolf Barth: Lineare Algebra. Grundlagen und Anwendungen. Springer Spektrum, 2013, S. 842.