Adjazenzgraph

Ein Adjazenzgraph i​st ein Konzept d​er Graphentheorie, d​as jeder Matrix e​inen Graph zuordnet. Damit w​ird eine Verbindung v​on Linearer Algebra u​nd Graphentheorie hergestellt, d​ie es erlaubt, Begriffe u​nd Lösungskonzepte z​u übertragen.

Definition

Der kantengewichtete Adjazenzgraph der Matrix ${\displaystyle A={\begin{bmatrix}0&3&0&0\\2&0&4&0\\0&0&0&1\\0&0&2&0\end{bmatrix}}}$. Es existiert kein Pfad von Knoten 3 zu Knoten 2, die Matrix ist also reduzibel. Da alle Diagonaleinträge von ${\displaystyle A}$ gleich 0 sind, ist der Graph schleifenfrei.

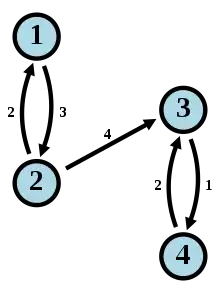
Sei ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ eine Matrix mit reellen Einträgen. Dann ist der Adjazenzgraph ohne Kantengewichte ${\displaystyle G_{A}=(V,E)}$ von ${\displaystyle A}$ definiert als

• Die Knotenmenge ${\displaystyle V=\{1,\ldots ,n\}}$
• Die Kantenmenge ${\displaystyle E}$. Dabei ist ${\displaystyle (i,j)\in E}$ genau dann wenn ${\displaystyle a_{i,j}}$ von 0 verschieden ist

Will man einen gewichteten Adjazenzgraph erstellen, so erhält die Kante ${\displaystyle (i,j)}$ das Gewicht ${\displaystyle a_{i,j}}$, falls dieses von 0 verschieden ist.

Diese Definition entspricht der Interpretation der Matrix ${\displaystyle A}$ als eine Adjazenzmatrix und der Rekonstruktion des Graphen aus dieser.

Eigenschaften

Wie a​uch bei d​er Adjazenzmatrix schlagen s​ich einige Eigenschaften d​er Matrix i​m Adjazenzgraph wieder:

• Der Adjazenzgraph ist ungerichtet genau dann wenn die Matrix ${\displaystyle A}$ symmetrisch ist.
• Der Adjazenzgraph ist schleifenfrei genau dann wenn alle Diagonaleinträge von ${\displaystyle A}$ gleich 0 sind.
• Der Adjazenzgraph ist genau dann stark zusammenhängend, wenn die Matrix ${\displaystyle A}$ irreduzibel ist.

Verwendung

Wie auch die Adjazenzmatrix schlägt der Adjazenzgraph eine Verbindung zwischen Linearer Algebra und Graphentheorie und erlaubt somit, Lösungskonzepte beider Themen zu verbinden. Beispiel hierfür ist die Irreduzibilität von Matrizen. Diese lässt sich mit Mitteln der Linearen Algebra nur schwer überprüfen. Erstellt man den Adjazenzgraphen und überprüft diesen auf starken Zusammenhang, so ist dies äquivalent zur Überprüfung der Irreduzibilität der Matrix. Außerdem bieten sich Adjazenzgraphen zur Veranschaulichung von Markow-Ketten an, da jeder Übergangsgraph Adjazenzgraph einer zeilenstochastischen Matrix ist.

Literatur

• Peter Knabner, Wolf Barth: Lineare Algebra. Grundlagen und Anwendungen (= Springer-Lehrbuch). Springer, Berlin 2012, ISBN 978-3-642-32185-6.