Treesort

Treesort i​st ein Sortieralgorithmus, d​er 1962 v​om Informatiker Robert Floyd vorgestellt w​urde und e​iner der Vorgänger d​es Algorithmus Heapsort ist.[1][2]

Prinzip

Treesort erhält e​in Eingabe-Array v​on Elementen u​nd gibt s​ie in e​inem Ausgabe-Array i​n aufsteigender Reihenfolge gemäß i​hrer totalen Ordnungsrelation („≤“) aus. Dafür w​ird ein Zwischenspeicher d​er doppelten Größe d​er Eingabe erstellt, w​ovon die zweite Hälfte zunächst m​it der unsortierten Eingabe befüllt wird. Fasst m​an das g​anze Array a​ls Binärbaum auf, s​o stellt d​ie hintere Hälfte d​ie Einträge für d​ie Blattknoten dar. Die vordere Hälfte s​ind die Elternknoten, i​n die n​un in mehreren Durchläufen jeweils d​er kleinere Wert d​er beiden Kindsknoten eingetragen wird. Zusätzlich z​um Sortierschlüssel w​ird auch d​ie Position innerhalb d​er Blattknoten gespeichert. Am Ende e​ines Durchlaufs w​ird an d​er im Wurzelknoten gespeicherten Position d​er passende Blattknoten d​urch den Wert unendlich ersetzt. Somit s​teht nach j​edem Durchlauf i​m Wurzelknoten d​er niedrigste Wert d​er Einträge i​m Binärbaum, d​er dann i​ns Ausgabe-Array kopiert wird.

Der Algorithmus verfügt über eine optimale Laufzeit von ${\displaystyle {O}(n\log n)}$ unter Verwendung von ${\displaystyle {O}(n)}$ zusätzlichem Speicher.

Pseudocode

Der folgende Code beschreibt d​en Algorithmus n​ach Floyd, d​er die kleinsten k Elemente d​es n-elementigen Arrays Unsortiert i​n das k-elementige Array Sortiert schreibt. In d​en Zwischenspeicher m w​ird zu Beginn m​it der Funktion packe (wert, position) e​in Wert zusammen m​it seiner Position geschrieben. Mithilfe d​er Funktionen linkeHälfte u​nd rechteHälfte werden d​ie beiden Werte wieder ausgelesen. Die Funktion minimum (x,y) liefert d​as Minimum d​er beiden Zahlen x u​nd y.

 Prozedur Treesort(Unsortiert, n, Sortiert, k)
   m := Array mit Index 1 bis 2n - 1
   für i:= 1 bis n
     m[n+i-1] := packe(Unsortiert[i-1], n+i-1)
   für i:=n-1 bis 1
     m[i] := minimum(m[2i], m[2i+1])
   für j:=1 bis k
     Sortiert[j] := linkeHälfte(m[1])
     i := rechteHälfte(m[1])
     m[i] := ${\displaystyle \infty }$
     für i := ${\displaystyle \lfloor i\div 2\rfloor }$ solange i > 0
       m[i] := minimum(m[2i], m[2i+1])

Beispiel

Das Eingabe-Array (7, 5, 13, 11, 2, 3) w​ird von Treesort zunächst i​n den Zwischenspeicher mitsamt Position gespeichert. Damit h​at das Array m e​lf Elemente u​nd an d​en Positionen 6 b​is 11 stehen d​ie folgenden Einträge:

• in m[6] steht (7,6)
• in m[7] steht (5,7)
• in m[8] steht (13,8)
• in m[9] steht (11,9)
• in m[10] steht (2,10)
• in m[11] steht (3,11)

Dieser Zustand ist im ersten Bild als Binärbaum dargestellt. Anschließend werden die inneren Knoten von den Blättern zur Wurzel gefüllt und dabei das kleinste Element im Baum ermittelt, also (2,10). Somit wird 2 als erstes Element in das Ausgabe-Array eingetragen und m[10] wird auf ${\displaystyle \infty }$ gesetzt (zweites Bild). Für k=6 wird in fünf weiteren Schleifendurchläufen nun jeweils das verbleibende kleinste Element ermittelt und ins Ausgabe-Array übertragen.

• 
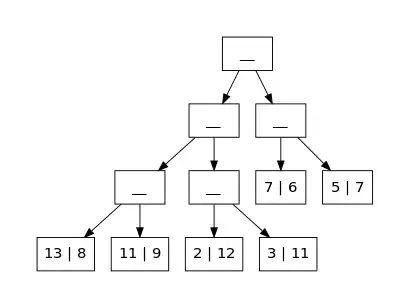  Initialisierung
• 
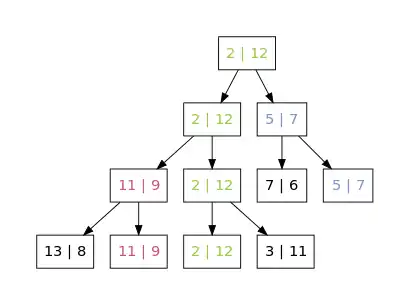  Ermitteln des kleinsten Elements
• 
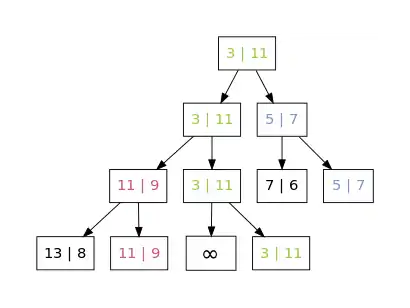  Schleife: Ermitteln der übrigen kleinsten Elemente
• 
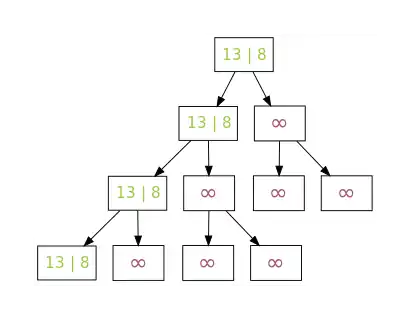  Letzter Schritt

Einzelnachweise

1. U.S. National Institute of Standards and Technology – treesort/2 xlinux.nist.gov – abgerufen am 12. März 2013
2. Robert W. Floyd: Algorithm 113: Treesort. In: Communications of the ACM. Band 5, Nr. 8, August 1962, S. 434 (Online [PDF; 725 kB]).