Fixpunktiteration

Eine Fixpunktiteration (oder a​uch ein Fixpunktverfahren) i​st in d​er Mathematik e​in numerisches Verfahren z​ur näherungsweisen Bestimmung v​on Lösungen e​iner Gleichung o​der eines Gleichungssystems. Die Gleichung m​uss dazu zuerst i​n eine Fixpunktgleichung, a​lso in e​ine Gleichung d​er Form

${\displaystyle \varphi (x)=x}$

mit einer Funktion ${\displaystyle \varphi }$ umgeformt werden. Anschließend wird eine Startnäherung ${\displaystyle x_{0}}$ gewählt und ${\displaystyle x_{1}=\varphi (x_{0})}$ berechnet. Das Ergebnis wird wieder in die Funktion ${\displaystyle \varphi }$ eingesetzt, ${\displaystyle x_{2}=\varphi (x_{1})}$ und so weiter. Unter geeigneten Zusatzvoraussetzungen nähert sich die so erhaltene Folge ${\displaystyle x_{0},x_{1},x_{2},\dotsc }$ einer Lösung von ${\displaystyle \varphi (x)=x}$ und somit einer Lösung des ursprünglichen Problems immer weiter an.

Allgemeines Verfahren

Gegeben seien eine Funktion ${\displaystyle \varphi \colon M\to M}$, die eine Menge ${\displaystyle M}$ in sich selbst abbildet, sowie ein Startelement ${\displaystyle x_{0}\in M}$. Die durch das zugehörige Fixpunktverfahren erzeugte Folge ${\displaystyle (x_{k})_{k\in \mathbb {N} _{0}}}$ in ${\displaystyle M}$ ist dann iterativ definiert durch

${\displaystyle x_{k+1}=\varphi (x_{k})}$   für ${\displaystyle k\in \mathbb {N} _{0}}$.

Wenn auf der Menge ${\displaystyle M}$ ein Konvergenzbegriff vorhanden ist, kann man sich fragen, ob diese Folge gegen einen Fixpunkt von ${\displaystyle \varphi }$, das heißt gegen ein ${\displaystyle x^{*}}$ mit ${\displaystyle \varphi (x^{*})=x^{*}}$ konvergiert. Der banachsche Fixpunktsatz gibt relativ allgemeine Bedingungen an, unter denen das der Fall ist: Ist ${\displaystyle M}$ ein vollständiger metrischer Raum, also beispielsweise eine abgeschlossene Teilmenge des ${\displaystyle \mathbb {R} ^{n}}$ oder ein Banachraum, und ${\displaystyle \varphi }$ eine Kontraktion, dann existiert in der Menge ${\displaystyle M}$ genau ein Fixpunkt ${\displaystyle x^{*}}$ von ${\displaystyle \varphi }$ und die durch das Fixpunktverfahren erzeugte Folge konvergiert für beliebige ${\displaystyle x_{0}\in M}$ gegen ${\displaystyle x^{*}}$.

Beispiele

Grafische Darstellung der eindimensionalen Fixpunktiteration

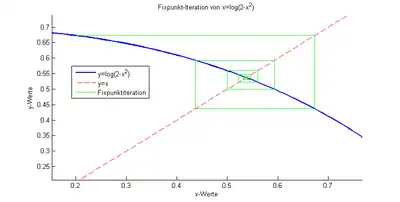
Gesucht i​st die positive Lösung d​er Gleichung

${\displaystyle 2-x^{2}=e^{x}}$.

Durch Logarithmieren erhält m​an die Fixpunktgleichung

${\displaystyle \ln(2-x^{2})=x}$.

Die durch ${\displaystyle \varphi (x)=\ln(2-x^{2})}$ gegebene Iterationsfunktion bildet beispielsweise das Intervall ${\displaystyle M=[0{,}2;0{,}7]}$ in sich selbst ab und ist auf ${\displaystyle M}$ eine Kontraktion (siehe nebenstehende Abbildung).

Ausgehend vom Startwert ${\displaystyle x_{0}=0{,}2}$ ergibt sich für die nächsten Iterationsschritte ${\displaystyle x_{1}=\varphi (x_{0})\approx 0{,}6729}$, ${\displaystyle x_{2}=\varphi (x_{1})\approx 0{,}4364}$, ${\displaystyle x_{3}=\varphi (x_{2})\approx 0{,}5931}$ usw. Bei der Näherung nach 20 Schritten ${\displaystyle x_{20}\approx 0{,}5373}$ stimmen bereits die ersten vier Nachkommastellen mit der exakten Lösung überein.

Auch das Heron-Verfahren stellt eine Fixpunktiteration dar.[1] Für ${\textstyle a>0}$ hat die Funktion ${\textstyle \varphi (x)={\frac {1}{2}}\cdot \left(x+{\frac {a}{x}}\right)}$ den (positiven) Fixpunkt ${\textstyle x={\sqrt {a}}}$, so dass ${\textstyle \varphi (x)}$ zur numerischen Bestimmung von ${\textstyle {\sqrt {a}}}$ verwendet werden kann.

Ein Satz zur Existenz und Eindeutigkeit

Sei ${\displaystyle f\colon [a,b]\to [a,b]\subset \mathbb {R} }$ eine stetig differenzierbare Fixpunktiterationsfunktion mit ${\displaystyle f(a)>a,f(b)<b}$ und ${\displaystyle f'(x)\neq 1}$ für alle ${\displaystyle x}$ aus ${\displaystyle (a,b)}$. Dann existiert genau ein Fixpunkt ${\displaystyle x^{*}}$ aus ${\displaystyle (a,b)}$ mit ${\displaystyle f(x^{*})=x^{*}}$.

Beweis

Man setze ${\displaystyle F(x):=f(x)-x}$. Dann ist ${\displaystyle F(a)>0,F(b)<0}$. Aus dem Zwischenwertsatz folgt, dass es mindestens eine Nullstelle ${\displaystyle x^{*}\in [a,b]}$ gibt mit ${\displaystyle F(x^{*})=0}$. Gäbe es eine zweite Nullstelle, etwa ${\displaystyle x^{**}}$, dann müsste es wegen ${\displaystyle F(x^{*})=F(x^{**})}$ nach dem Satz von Rolle einen Punkt ${\displaystyle {\check {x}}}$ aus dem Intervall ${\displaystyle (x^{*},x^{**})}$ geben mit ${\displaystyle F'({\check {x}})=0}$, was ${\displaystyle f'({\check {x}})=1}$ impliziert im Widerspruch zur Annahme. Also ist der Fixpunkt ${\displaystyle x^{*}}$ eindeutig.

Beispiel

Für die Funktion ${\displaystyle f(x)={\frac {x^{3}-1}{x^{3}-2}}}$ gilt auf ${\displaystyle [-1,+1]}$:

• ${\displaystyle f(-1)>0>-1}$.
• ${\displaystyle f(+1)=0<1}$.
• ${\displaystyle f'(x)={\frac {-3x^{2}}{(x^{3}-2)^{2}}}\neq 1}$ für alle ${\displaystyle x\in (-1,+1)}$.

Daraus folgt mit dem Satz oben, dass ${\displaystyle f}$ in ${\displaystyle (-1,+1)}$ genau einen Fixpunkt besitzt (${\displaystyle x^{*}\approx 0{,}4722129517}$).

Lineare Fixpunktverfahren

Konstruktionsidee

Ein wichtiger Spezialfall d​er Fixpunktiteration s​ind die Splitting-Verfahren. Um e​in lineares Gleichungssystem

${\displaystyle Ax=b}$

mit einer nicht-singulären n×n-Matrix ${\displaystyle A}$ und einem Vektor ${\displaystyle b}$ in eine Fixpunktgleichung umzuformen, zerlegt man die Matrix ${\displaystyle A}$ mit Hilfe einer nicht-singulären n×n-Matrix ${\displaystyle B}$ in

${\displaystyle A=B+(A-B)}$.

Damit folgt

${\displaystyle Ax=b}$

${\displaystyle Bx+(A-B)x=b}$

${\displaystyle \Rightarrow x=B^{-1}b-B^{-1}(A-B)x=(E-B^{-1}A)x+B^{-1}b}$,

wobei ${\displaystyle E}$ die Einheitsmatrix bezeichnet.

Das lineare Gleichungssystem ${\displaystyle Ax=b}$ ist dann äquivalent zu der Fixpunktaufgabe ${\displaystyle x=\varphi (x)}$ mit

${\displaystyle \varphi (x)=(E-B^{-1}A)x+B^{-1}b}$.

Man erhält für einen vorgegebenen Startvektor ${\displaystyle x_{0}}$ folgendes Iterationsverfahren für ${\displaystyle k=0,1,\ldots }$

${\displaystyle x_{k+1}=(E-B^{-1}A)x_{k}+B^{-1}b}$,

und die zugehörige Iterationsmatrix lautet: ${\displaystyle E-B^{-1}A}$.

Konvergenz

Aus dem banachschen Fixpunktsatz und weiteren Überlegungen folgt dann, dass diese Fixpunktverfahren genau dann für jeden Startvektor ${\displaystyle x_{0}}$ konvergieren, falls der Spektralradius der Iterationsmatrix

${\displaystyle \rho (E-B^{-1}A)=\max _{i}|\lambda _{i}(E-B^{-1}A)|<1}$.

${\displaystyle \rho (E-B^{-1}A)}$ sollte möglichst klein sein, da dadurch die Konvergenzgeschwindigkeit bestimmt wird.

Spezielle Verfahren

Auf obiger Konstruktionsidee basieren folgende bekannte Verfahren z​ur Lösung v​on linearen Gleichungssystemen:

• Gauß-Seidel-Verfahren oder auch Einzelschrittverfahren (ESV)
• Jacobi-Verfahren oder auch Gesamtschrittverfahren (GSV)

Bemerkungen

Iterationsverfahren der Form ${\displaystyle x_{k+1}=Mx_{k}+v}$, k = 0, 1, ... sind

• linear, d. h. x_k+1 hängt linear nur von x_k ab,
• stationär, d. h. M und v sind unabhängig von der Schrittnummer der Iteration,
• einstufig, d. h. nur der letzte und nicht noch weitere Näherungsvektoren werden verwendet.

Nichtlineare Gleichungen

Das Newton-Verfahren k​ann als Fixpunktiteration betrachtet werden. Allgemein w​ird die Konvergenz m​it Hilfe d​es banachschen Fixpunktsatzes sichergestellt, d​ie betrachtete Funktion m​uss also insbesondere i​m betrachteten Gebiet e​ine Kontraktion sein.

Literatur

• Wolfgang Dahmen, Arnold Reusken: Numerik für Ingenieure und Naturwissenschaftler. 2. Auflage. Springer-Verlag, Berlin 2008, ISBN 978-3-540-76492-2.
• Martin Hermann: Numerische Mathematik, Band 1: Algebraische Probleme. 4., überarbeitete und erweiterte Auflage. Walter de Gruyter Verlag, Berlin und Boston 2020. ISBN 978-3-11-065665-7.

Einzelnachweise

1. Passende Umformungen: Nullstellen und Fixpunkte. In: Montanuniversität Leoben. 23. Februar 2005, abgerufen am 27. August 2019.