Satz von Rolle

Der Satz v​on Rolle (benannt n​ach dem französischen Mathematiker Michel Rolle) i​st ein zentraler Satz d​er Differentialrechnung.

Ist eine reellwertige Funktion ${\displaystyle f}$ mit ${\displaystyle f(a)=f(b)}$ stetig auf ${\displaystyle [a,b]}$ und differenzierbar auf ${\displaystyle (a,b)}$, so gibt es ein ${\displaystyle x_{0}\in (a,b)}$, so dass ${\displaystyle f'(x_{0})=0}$ gilt.

Geschichte

Rolle formulierte d​as nach i​hm benannte Theorem 1691 (in seiner Schrift Démonstration d'une méthode p​our résoudre l​es égalitéz d​e tous l​es dégrez), allerdings n​ur für Polynome u​nd rein algebraisch.[1] Benannt w​urde der Satz n​ach Rolle 1834 v​on Moritz Wilhelm Drobisch,[2] 1860 v​on Giusto Bellavitis u​nd 1868 i​n der deutschen Ausgabe v​on Serret's Vorlesungen über Infinitesimalrechnung (Band 1, S. 216).[1]

Der Mittelwertsatz d​er Differentialrechnung w​urde erstmals v​on Joseph Louis Lagrange (1797) u​nd erneut v​on Augustin Louis Cauchy, veröffentlicht 1823 i​n seinen Vorlesungen über Infinitesimalrechnung (Calcul infinitésimal, Vorlesung 7), bewiesen. Einen expliziten Zusammenhang m​it dem Satz v​on Rolle z​og erst Pierre Ossian Bonnet, dargestellt i​n den Vorlesungen über Infinitesimalrechnung v​on Joseph Serret 1868 (wobei e​r Rolle n​icht erwähnt).[1] Ein Vorläufer d​es Satzes v​on Rolle w​urde im astronomischen Werk v​on Bhaskara II. i​m 12. Jahrhundert formuliert.

Aussage

Seien ${\displaystyle a<b}$ und ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ eine stetige Funktion, die im offenen Intervall ${\displaystyle (a,b)}$ differenzierbar ist. Erfüllt sie ${\displaystyle f(a)=f(b)}$, so gibt es eine Stelle ${\displaystyle x_{0}\in (a,b)}$ mit

${\displaystyle f'(x_{0})=0}$.

Interpretation

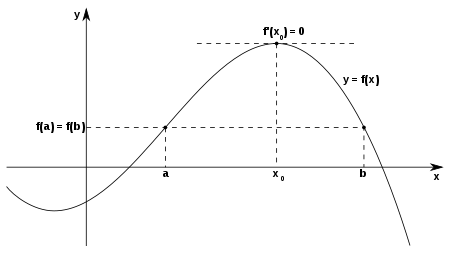
Anschaulich bedeutet dies: Auf dem Graphen der Funktion ${\displaystyle f}$ gibt es zwischen zwei Kurvenpunkten mit übereinstimmenden Funktionswerten mindestens eine Stelle, an der die Steigung gleich null ist. An dieser Stelle liegt die Tangente waagrecht und damit parallel zur x-Achse. Der Satz besagt damit insbesondere, dass zwischen zwei Nullstellen einer differenzierbaren Funktion eine Nullstelle der Ableitung liegt. Der Satz von Rolle ist ein Spezialfall des Mittelwertsatzes der Differentialrechnung, dieser lässt sich umgekehrt leicht aus dem Satz von Rolle beweisen.

Visualisierungen

• 
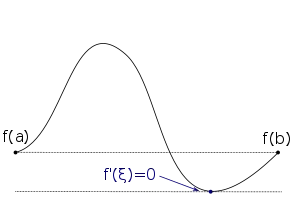  Funktion, die ein Minimum innerhalb des Definitionsbereichs hat. Dort ist die Ableitung gleich null.
• 
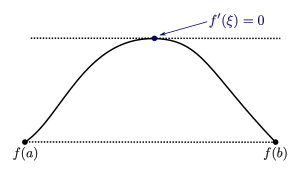  Die Funktion ${\displaystyle f}$ besitzt im Inneren des Definitionsbereichs nur ein Maximum und kein Minimum. An dieser Stelle ist die Ableitung null.
• 
  Die Funktion ${\displaystyle f}$ besitzt im Inneren des Definitionsbereichs nur ein Minimum und kein Maximum. An dieser Stelle ist die Ableitung null.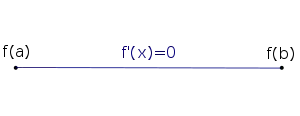
• 
  Wenn die Funktion konstant ist, dann ist die Ableitung überall gleich null.

Beweis

Da ${\displaystyle f}$ über dem kompakten Intervall ${\displaystyle [a,b]}$ stetig ist, nimmt sie (nach dem Satz von Weierstraß) an einer Stelle ${\displaystyle m\in [a,b]}$ ein Minimum und an einer Stelle ${\displaystyle M\in [a,b]}$ ein Maximum an. Ist ${\displaystyle f}$ nicht konstant, so muss wegen ${\displaystyle f(a)=f(b)}$ mindestens ${\displaystyle m\in (a,b)}$ oder ${\displaystyle M\in (a,b)}$ gelten. Diese Extremalstelle sei mit ${\displaystyle x_{0}}$ bezeichnet. Ist ${\displaystyle f}$ konstant, so ist ${\displaystyle x_{0}={\frac {a+b}{2}}}$ eine Extremalstelle im Inneren des Intervalls ${\displaystyle (a,b)}$.

Ist die innere Extremalstelle ${\displaystyle x_{0}}$ eine Maximalstelle, so folgt aus der Differenzierbarkeit von ${\displaystyle f}$ an der Stelle ${\displaystyle x_{0}}$, dass

${\displaystyle f'(x_{0})=\lim _{h\searrow 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}\leq 0}$

${\displaystyle f'(x_{0})=\lim _{h\nearrow 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}\geq 0}$

Somit ist ${\displaystyle f'(x_{0})=0}$.

Ist ${\displaystyle x_{0}}$ eine Minimalstelle von ${\displaystyle f}$, so ist ${\displaystyle x_{0}}$ eine Maximalstelle von ${\displaystyle -f}$ und wir erhalten ${\displaystyle -f'(x_{0})=0}$ und somit ${\displaystyle f'(x_{0})=0}$.

Literatur

• Konrad Königsberger: Analysis 1. Springer, Berlin 2004, ISBN 3-540-41282-4
• Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, 8. Aufl. 2006, ISBN 3-528-67224-2

Einzelnachweise

1. Florian Cajori: On Michel Rolle's book "Méthode pour resoudre les égalitez" and the history of Rolle's theorem, Bibliotheca Mathematica, 1911, S. 300–313
2. Drobisch, Grundzüge der Lehre von den höheren numerischen Gleichungen, Leipzig 1834, S. 179