Fitts’ Gesetz

Fitts’ Gesetz (oder Fitts‘ Law und Fitts’s Law (Englisch) genannt) ist ein prädiktives Modell, welches die Dauer für menschliche Bewegungen bei Zeigeaufgaben vorhersagt. Dabei verwendet es die Distanz zum Ziel, sowie dessen Größe als Parameter.[1] Das Modell wird häufig im Bereich der Mensch-Computer-Interaktion und Ergonomie verwendet, um beispielsweise Layouts oder Eingabegeräte zu vergleichen.

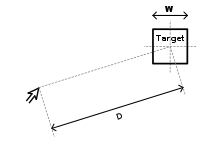
Fitts’ Gesetz; Darstellung der Zielgröße W und Distanz D

Das Gesetz beschreibt die benötigte Zeit, um schnell und direkt von einem Punkt auf ein Ziel zu zeigen. Diese ergibt sich aus einer Funktion, welche die Größe des Ziels ins Verhältnis zur Distanz vom Startpunkt aus setzt. Fitts’ Gesetz wird verwendet, um die Aktion der Zielauswahl modellhaft in verschiedenen Kontexten zu beschreiben. Dazu zählen zum einen das physische Berühren des Objekts mit der Hand oder einem Finger, aber auch virtuelle Interaktionen, wie bei der Verwendung eines Zeigegerätes in Verbindung mit einem Computermonitor. Allgemein zeigt das Modell, dass es für den Nutzer schwieriger wird ein Ziel zu treffen, je weiter entfernt oder kleiner es ist.

Fitts’ Gesetz hat seine Voraussagekraft in unterschiedlichsten Bedingungen unter Beweis gestellt. So kann es für verschiedene Extremitäten (Hände, Finger, Füße[2] die untere Lippe,[3]) verwendet werden, aber auch für Kopfbewegungen[4]. Zudem gilt es auch bei verschiedenen Eingabegeräten.[5] Das Gesetz findet auch in Unterwasserszenarios[6] Anwendung. Auch bei breiten Anwendergruppen (jung, alt, männlich, weiblich[7]), Personen mit sonderpädagogischen Bedürfnissen[8] und bei Personen unter Drogeneinfluss[9] ist das Gesetz gültig.

Ursprüngliches Modell

Das ursprüngliche Paper von Paul Morris Fitts wurde 1954 veröffentlicht und stellt das Gesetz als eine Metrik zur Quantisierung der Schwierigkeit von Zielauswahlaufgaben vor. Diese Metrik basierte auf einer Analogie zur Informationstheorie, in der die Distanz zum Ziel (D) als Signalstärke und die Breite des Ziels (W) als Rauschen behandelt wurden. Daraus ergibt sich der Fitts-sche Schwierigkeitsindex (ID, index of difficulty) in Bit:

${\text{ID}}=\log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}$

Fitts' Aufgabe im Experiment

Fitts gab darüber hinaus noch einen Performanzindex (IP, index of performance) in Bit pro Sekunde an, um die Leistung des Nutzers darstellen zu können. Hierbei werden der Schwierigkeitsindex (ID) mit der ermittelten Bewegungszeit für die Auswahl des Ziels (MT, movement time) in Sekunden miteinander kombiniert. Laut Fitts wird definiert: „Die durchschnittliche Informationsrate erzeugt durch eine Abfolge von Bewegungen ist die durchschnittliche Information pro Bewegung geteilt durch die Dauer der Bewegung“.[1] Daraus folgt:

${\text{IP}}={\Bigg (}{\frac {\text{ID}}{\text{MT}}}{\Bigg )}$

Aktuelle Forschung verweist auf den Performanzindex auch als Durchsatz (TP, throughput). Zusätzlich wird die Genauigkeit beim Auswählen eines Ziels häufig mit in die Berechnung einbezogen.

Spätere Arbeiten nach Fitts erstellten Regressionsmodelle, die auf die Korrelation (r) für ihre Gültigkeit untersucht wurden. Die letztlich daraus entstandene Formel beschreibt einen linearen Zusammenhang zwischen der Bewegungsdauer (MT) und dem Schwierigkeitsindex (ID), bestehend aus W und D, der Aufgabe:

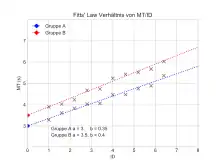
${\text{MT}}=a+b\cdot {\text{ID}}=a+b\cdot \log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}$

Darstellung des linearen Zusammenhangs in Fitts' Gesetz

Diese Formel ergibt sich aus:

MT ist die durchschnittliche Dauer zur Erfüllung der Bewegung zur Zielauswahl
a und b sind Konstanten in Bezug auf die Zeit, welche vom verwendeten Eingabegerät abhängen. Diese werden meist empirisch, über mehrere Versuchsdurchläufe und anschließender Regressionsanalyse, bestimmt. a definiert den Y-Achsenschnittpunkt und beschreibt die Verzögerung bis die Bewegung beginnt. Der zweite Parameter b, die Steigung, kann als Beschleunigung interpretiert werden. Hierbei wird der häufig beobachtete lineare Zusammenhang zwischen Dauer und Schwierigkeit deutlich.[10]
ID ist der berechnete Schwierigkeitsindex
D ist die Distanz vom Startpunkt der Aufgabe zum Mittelpunkt des Ziels
W ist die Breite des Ziels entlang der Bewegungsachse. So wird auch die Fehlertoleranz beschrieben, da die Zielbewegung innerhalb ±^W⁄₂ vom Zielmittelpunkt fallen muss.

Da Eingaben auf kürzere Bewegungszeiten optimiert werden sollten, können die zu bestimmenden Parameter a und b als Performanzindikatoren für die getesteten Eingabegeräte benutzt werden. Card, Englisch und Burr[11] verwendeten das Gesetz als Erste im Bereich der Mensch-Computer-Interaktion. Sie interpretierten ¹⁄_b als eigenen Performanzindex (IP, index of performance), um verschiedene Eingabegeräte miteinander zu vergleichen. Hierbei erwies sich die Computermaus besser als der Joystick oder Richtungstasten.[11] Laut Stuart Cards Biografie war diese Entdeckung „ein großer Einflussfaktor zur kommerziellen Einführung der Maus durch Xerox“.[12]

Experimente mit Fitts Gesetz werden meist mit Variationen von entweder Distanz oder Zielbreite durchgeführt, aber selten beider Parameter. Die Vorhersagekraft des Gesetzes verschlechtert sich bei Veränderung beider Parameter über große Wertebereiche.[13] Anzumerken ist, dass die Schwierigkeit (ID) nur über das Verhältnis von Distanz zu Zielbreite abhängig ist. Daraus folgt, dass Aufgaben sich unendlich groß skalieren lassen müssten und dabei dieselbe Schwierigkeit und Ausführungsdauer beibehalten, was praktisch nicht möglich ist. Abgesehen von diesen Fehlern, verfügt das Modell über eine außergewöhnliche belastbare Vorhersagekraft. Deshalb wird es in verschiedensten Bereichen, Computerinterfacemodalitäten und Bewegungsaufgaben verwendet und liefert Erkenntnisse im Bereich des Interface-Designs.

Bewegungen

Eine Bewegung nach Fitts‘ Gesetz lässt sich vereinfacht in zwei Bewegungsphasen[10] unterteilen:

Anfangsbewegung (initial movement). Sie ist schnell, grob und in Richtung des Zielobjektes.
Endbewegung (final movement). Sie verlangsamt sich zunehmend und ist dazu da, das Ziel genau zu erreichen.

Die erste Phase wird primär durch den Abstand des Ziels bestimmt. In dieser Phase wird sich schnell, jedoch unpräzise dem Ziel angenähert. Die zweite Phase bestimmt die Genauigkeit, mit der das Ziel getroffen wird. Nun muss sich kontrolliert zur kleinen Zielfläche bewegt werden. Das Gesetz besagt nun, dass die Dauer der Aufgabe linear abhängig zur Schwierigkeit ist[10]. Da Aufgaben jedoch dieselbe Schwierigkeit bei unterschiedlichen Größen haben können, gilt allgemein auch, dass die Distanz mehr Auswirkung auf die Dauer hat als die Breite.

Häufig wird auch Eye-Tracking als mögliches Anwendungsgebiet für Fitts‘ Law genannt. Dies ist jedoch zumindest umstritten[14]. Aufgrund der hohen Geschwindigkeit bei Sakkadenbewegungen, ist das Auge während diesen blind. Somit ist die Zielsuche des Blickes nicht analog zu beispielsweise Handbewegungen, da die erste Phase blind geschieht.

Bits pro Sekunde: Innovation angeführt durch Informationstheorie

Die meistverbreitete Variante zur Berechnung des Schwierigkeitsindex (ID, index of difficulty) in der Mensch-Computer-Interaktion ist die Shannon-Form:

${\text{ID}}=\log _{2}{\Bigg (}{\frac {D}{W}}+1{\Bigg )}$

Scott MacKenzie, Professor an der York-Universität, stellte diese Form vor.[15] Der Name bezieht sich auf die formal ähnliche Formel des Shannon-Hartley-Gesetz.[16] Dieses beschreibt die Übertragung von Information bei gegebener Bandbreite, Signalstärke und Rauschen. In Fitts‘ Gesetz entspricht die Distanz der Signalstärke und die Zielbreite dem Rauschen.

Die Schwierigkeit einer Aufgabe wird in Bit pro Sekunde angegeben. Damit wird die Menge an Information beschrieben. Dies begründet sich in der Annahme, dass Zeigen eine Informationsverarbeitungsaufgabe ist. Trotz des Fehlens eines mathematisch beweisbaren Zusammenhangs zwischen Fitts‘ Gesetz und dem Shannon-Hartley-Theorem, wird diese Form in der aktuellen Forschung verwendet, da sich die Bewegungen mittels des informationstheoretischen Konzepts darstellen lassen. Seit 2002 wird diese Form auch in der ISO 9241 genannt und definiert so den Standard für Tests von Mensch-Maschine-Schnittstellen. In einem theoretischen Experiment hat sich jedoch gezeigt, dass der Fitts-sche Schwierigkeitsindex und die zugrunde liegende informationstheoretische Shannon-Entropie unterschiedliche Bit-Werte für die zu übertragende Information ergeben.[17] Die Autoren nennen den Unterschied der beiden Berechnungsarten vernachlässigbar. Lediglich bei Vergleichen von Geräten deren Eingabeentropie bekannt ist oder der Bewertung menschlicher Informationsverarbeitung, würde die Formel zu Fehlern führen.

Anpassungen für Genauigkeiten: Einbezug der effektiven Zielbreite

Crossman veröffentlichte im Jahr 1956[18] eine Ergänzung, welche von Fitts selbst in einer Veröffentlichung mit Peterson im Jahr 1964 genutzt wurde[19]. Hierbei wird die Breite (W) des Ziels durch seine effektive Breite (W_e) ersetzt. W_e ergibt sich aus der Standardabweichung der Trefferkoordinaten über den Verlauf eines Versuchs mit konkreten D-W-Werten. Wird die Auswahl des Nutzers beispielsweise als x-Koordinaten entlang der Bewegungsachse erfasst, so ergibt sich:

$W_{e}=4.133\times SD_{x}$

Daraus folgt über die Shannon-Form:

${\text{ID}}_{e}=\log _{2}{\Bigg (}{\frac {D}{W_{e}}}+1{\Bigg )}$

Und schließlich kann ein angepasster Performanzindex berechnet werden, wobei MT mit der vollen Breite berechnet wird:

${\text{IP}}={\Bigg (}{\frac {ID_{e}}{MT}}{\Bigg )}$

Sind die Koordinaten der Auswahl normalverteilt, zieht sich W_e über 96 % der Werteverteilung. Wurde nun im Experiment eine Fehlerrate von 4 % beobachtet so ist W_e = W. Ist die Fehlerrate höher so gilt W_e > W, ist sie geringer, so ist W_e < W. Durch den Einbezug der effektiven Zielbreite gibt Fitts‘ Gesetz genauer wieder, worauf der Nutzer eigentlich gezielt hat und nicht das vom Experiment angebotene Ziel. So liegt der Nutzen den Performanzindex mit effektiver Breite zu berechnen darin, dass die Genauigkeit und somit der Raum ein Ziel zu treffen, miteinbezogen wird. Die Relation von Geschwindigkeit zu Genauigkeit wird so genauer dargestellt. Diese Formel wird auch in ISO 9241-9 als Referenz zur Berechnung des Durchsatzes (TP, throughput) angegeben.

Welfords Modell

Kurz nach der Vorstellung der ursprünglichen Modells, wurde eine 2-Faktorenvariation vorgestellt. Hier wird nun zwischen dem Einfluss der Breite des Ziels und dem Einfluss durch den Abstand zum Ziel auf die Bewegungsdauer unterschieden. Welfords Modell, vorgestellt im Jahr 1968, teilt die Parameter der Distanz und Breite in zwei unabhängige Terme auf. So werden die gegenseitigen Einflüsse voneinander getrennt. Dieses Modell zeigt eine verbesserte Vorhersagekraft:[18]

$T=a+b_{1}\log _{2}(D)+b_{2}\log _{2}(W)$

Da das Modell nun einen weiteren Parameter hat, kann die Genauigkeit der Vorhersage nicht mit der Einfaktorform des ursprünglichen Fitts‘ Gesetz verglichen werden. Jedoch kann das neue Modell, ähnlich wie bei der Shannon-Form, angepasst werden:

$T=a+b_{1}\log _{2}(D+W)+b_{2}\log _{2}(W)=a+b\log _{2}\left({\frac {D+W}{W^{k}}}\right)$

Der zusätzliche Parameter k erlaubt es Winkel der Bewegung und des Ziels in das Modell einzubeziehen. So wird die Position des Nutzer relativ zur Oberfläche einbezogen. Der Exponent gewichtet den Einfluss von Bewegungswinkel zu Zielwinkel. Diese Formulierung wurde von Kopper et al. vorgestellt.[20] Ist k=1, so kann das Modell mit dem F-Test für verschachtelte Modelle direkt mit der Shannon-Form des Fitts’ Gesetz verglichen werden.[21] Vergleiche ergeben, dass die Shannon-Form von Welfords Modell bessere Voraussagen liefert und zudem auch robuster auf Variation im Control-Display-Gain (Verhältnis der Bewegung der Eingabe zur Bewegung des Eingabegerätes). Daraus folgt, obwohl die Shannon-Form komplexer und weniger intuitiv ist, beschreibt sie das empirisch beste Modell für die Evaluation für virtuelle Zeigeaufgaben.

Erweiterung des Modells von Eindimensionalität zur Mehrdimensionalität und weitere Aspekte

Erweiterung auf mehrere Dimensionen

In seiner ursprünglichen Form sollte Fitts’ Gesetz nur auf eindimensionale Aufgaben angewandt werden. Jedoch mussten die Probanden im Ursprungsexperiment mehrere Styli mit unterschiedlichen Gewichten in 3 Dimensionen von einer Metallplatte zu einer anderen bewegen, was auch als reziproke Antipp-Aufgabe bezeichnet wird.[1] So war die Breite des Ziels senkrecht zur Bewegungsrichtung, um deren Einfluss gering zu halten. Fitts’ Gesetz wird nun aber meist für Aufgaben auf Computermonitoren verwendet, in deren Kontext die Ziele in zwei Dimensionen ausgeprägt sind (Höhe und Breite).

Reziproke Antippaufgabe in 2D

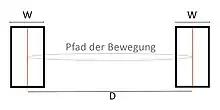
Um das Gesetz an diesen Kontext anzupassen gibt es zwei Möglichkeiten. Für Aufgaben in hierarchischen, aufklappenden Menüstrukturen muss der Nutzer einen Pfad gegeben durch das Layout befahren. Hierzu wird das Accot-Zhai-Steering-Gesetz angewandt.

Bei sonstigen einfachen Zeigeaufgaben zeigt sich das Gesetz als robust. Jedoch sollten Anpassungen vorgenommen werden, um Fehlerraten und die Geometrie der Ziele konsistent zu erfassen.[22][23] Hierfür gibt es verschiedene Möglichkeiten die Größe zu berechnen[24]:

Status Quo: Horizontale Breite des Ziels messen
Summenmodell: W ist Höhe zur Breite addieren
Flächenmodell: W ist Höhe mal Breite
Kleineres von beiden: W ist der kleinere Wert von Höhe oder Breite
W-Modell: W ist die Länge des Ziels in Bewegungsrichtung gemessen (effektive Größe)

Die Literatur verwendet dabei überwiegend das W-Modell.

Charakterisierung der Performanz

Da die Parameter a und b die Zeitparameter der Bewegung über verschiedene Zielanordnungen und -formen erfassen sollen, können diese auch als Performanzindikatoren für das evaluierte Nutzerinterface dienen. Hierbei muss die Varianz der unterschiedlichen Nutzer von der Varianz der unterschiedlichen Interfaces getrennt werden können. Der Parameter a sollte positiv und nahe 0 liegen, jedoch kann er auch für die Evaluierung von Durchschnittswerten ignoriert werden. Der Parameter ist auch in Fitts‘ ursprünglicher Variante gleich Null.[17] Um die Parameter aus empirischen Versuchswerten zu bestimmen gibt es unterschiedliche Methoden. Da diese unterschiedlichen Methoden zu uneindeutigen Performanzergebnissen führen, die auch Unterschiede eliminieren können, ist dies ein strittiges Thema in der Forschung.[25][26]

Zudem fehlt dem Gesetz ein intrinsischer Fehlerterm. Nutzer, die aggressiv und schnell zwischen den Zielen springen erreichen diese schneller. Machen sie einen Fehler, muss lediglich eine Wiederholungen mehr gemacht werden. Da die Anzahl der Wiederholungen in der eigentlichen Formel keine Verwendung findet, wird dies in der Performanz nicht widergespiegelt. Die dadurch entstehende Fehlerrate sollte in das Modell miteinbezogen werden, da sonst die durchschnittliche Aufgabenzeit künstlich gesenkt wird.

Ziele mit zeitlicher Einschränkung

Fitts’ Gesetz wird bei Zielen mit räumlicher Dimension verwendet. Ziele können jedoch auch auf einer Zeitachse definiert sein, womit sie zeitlich begrenzte Ziele sind. Hierzu zählen blinkende Ziele oder Ziele die sich auf eine Auswahlfläche zu bewegen. Hierbei kann wie bei räumlichen Aufgaben die Distanz des Ziels (hier die zeitlich Distanz D_t) und dessen Breite (hier die zeitliche Breite W_t) definiert werden. Konkret bezeichnet D_t die Zeit, die der Nutzer warten muss, bis das Ziel erscheint und W_t die Zeit, in der das Ziel zu sehen ist. Im Beispiel für ein blinkendes Ziel beschreibt D_t die Zeit zwischen dem Blinken und W_t die Anzeigedauer bis zum nächsten Abblenden. Wie auch bei räumlichen Zielen wird die Auswahl bei kleiner Breite (W_t) oder größere Distanz (D_t) schwieriger, da das Ziel im temporalen Kontext kürzer angewählt werden kann.

Die Aufgabe des Auswählens von zeitlich begrenzten Zielen wird auch „temporales Zeigen“ genannt. Das gezeigte Modell wurde zuerst 2016 im Feld der Mensch-Computer-Interaktion veröffentlicht.[27] So kann die Performanz des menschlichen Nutzers beim temporalen Zeigen mit einer Funktion für den temporalen Index der Schwierigkeit angegeben werden (ID_t):

{\text{ID}}_{t}=\log _{2}{\Bigg (}{\frac {D_{t}}{W_{t}}}{\Bigg )}

Folgen für das UI-Design

Magische Ecken in Microsoft Windows

Radiales Menü

Aus der Formulierung von Fitts‘ Gesetz lassen sich Richtlinien für die Gestaltung von GUIs ableiten. Grundlegend sagt das Gesetz aus, dass ein Ziel so groß wie möglich sein soll, um einfacher getroffen werden zu können. Dies lässt sich aus dem W-Parameter des Schwierigkeitsindex ableiten. Spezifischer ist hier die effektive Größe des Ziels gemeint, welche entlang der Bewegungsrichtung des Nutzer durch das Ziel verläuft.

Um den D-Parameter zu optimieren, sollten Ziele, die im Kontext häufig miteinander verwendet werden, gruppiert werden.

Ziele, die an den Rändern eines klassischen Bildschirms platziert werden, sind theoretisch ideale Ziele, da sie in eine Dimension als unendlich groß angesehen werden können. Der Nutzer kann sein Zeigegerät am Rand des Bildschirms unendlich weit bewegen, ohne dass sich die Position des Cursors ändert. Somit ist die effektive Größe eines Ziels am Bildschirmrand unendlich. Diese Regel wird auch “Regel der unendlichen Kanten” genannt. Die Anwendung kann in Apples Desktopbetriebssystem macOS gesehen werden. Hier wird die Menüleiste eines Programms immer unabhängig vom Programmfenster an der oberen Bildschirmkante angezeigt.[28]

Die genannte Regel ist an den Ecken besonders effektiv. Hier führen zwei Kanten zusammen und können so eine unendlich große Fläche erzeugen. Microsoft Windows platziert seinen essentiellen “Start”-Knopf in der unteren linken Ecke und Microsoft Office 2007 nutzt die oberen linke Ecke für den funktionalen Office-Knopf. Die vier Ecken werden auch „magische Ecken“ genannt.[29] Trotz dieser Regel befindet sich der “Beenden”-Knopf in Microsoft Windows in der oberen rechten Ecke. So kann der Knopf zwar in Vollbildanwendungen leicht ausgewählt werden, aber auch einfacher unbeabsichtigt. macOS platziert den Knopf in der linken oberen Ecke des Programmfensters, wobei die Menüleiste die magische Ecke ausfüllt und der Knopf somit nicht angewählt wird.

UI-Layouts, die es ermöglichen, Menüs dynamisch an der Stelle des Mauszeiger zu erstellen, reduzieren die Bewegungsdistanz (D) und damit die Aufgabendauer nochmals. Nutzer können so Funktionen nahe der bisherigen Stelle ausführen. Somit muss kein neuer Bereich des UIs angesteuert werden. Dies wird von den meisten Betriebssystemen bei Kontextmenüs angewandt. Der Pixel, an dem das Menü beginnt, wird als „magischer Pixel“ bezeichnet.[24]

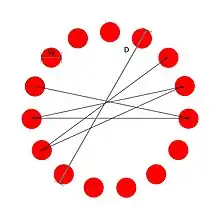
Boritz et al. (1991) verglichen radiale Menüs.[30] In diesen sind alle Funktionen als Kreissektoren und somit mit gleichen Abstand um den magischem Pixel angeordnet. Diese Arbeit zeigt, dass auch die Richtung, in die eine Bewegung ausgeführt wird, miteinbezogen werden sollte. Für Rechtshänder war das Auswählen von Funktionen auf der linken Seite des radialen Menüs schwieriger als bei Funktionen auf der rechten Seite. Oben und unten angeordnete Funktionen wurden jeweils gleich schnell erreicht.

Siehe auch

Johnny Accot, Shumin Zhai: More than dotting the i's—foundations for crossing-based interfaces, Proceedings of ACM CHI 2002 Conference on Human Factors in Computing Systems 2002, ISBN 978-1581134537, S. 73–80, doi:10.1145/503376.503390.
Johnny Accot, Shumin Zhai: Refining Fitts' law models for bivariate pointing, Proceedings of ACM CHI 2003 Conference on Human Factors in Computing Systems 2003, ISBN 978-1581136302, S. 193–200, doi:10.1145/642611.642646.
Stuart K. Card, Thomas P. Moran, Allen Newell: The Psychology of Human–Computer Interaction, (Free registration required), L. Erlbaum Associates, Hillsdale, NJ 1983, ISBN 978-0898592436.
Paul M. Fitts, James R. Peterson: Information capacity of discrete motor responses. In: Journal of Experimental Psychology. 67, Februar 1964, S. 103–112. doi:10.1037/h0045689.

Einzelnachweise

Paul M. Fitts: The information capacity of the human motor system in controlling the amplitude of movement. In: Journal of Experimental Psychology. 47, Nr. 6, Juni 1954, S. 381–391. doi:10.1037/h0055392. PMID 13174710.
Errol R. Hoffmann: A comparison of hand and foot movement times. In: Ergonomics. 34, Nr. 4, 1991, S. 397–406. doi:10.1080/00140139108967324. PMID 1860460.
Marcelo Archajo Jose, Roleli Lopes: Human-computer interface controlled by the lip. In: IEEE Journal of Biomedical and Health Informatics. 19, Nr. 1, 2015, S. 302–308. doi:10.1109/JBHI.2014.2305103. PMID 25561451.
R. H. Y. So, M. J. Griffin: Effects of target movement direction cue on head-tracking performance. In: Ergonomics. 43, Nr. 3, 2000, S. 360–376. doi:10.1080/001401300184468. PMID 10755659.
I. Scott MacKenzie, A. Sellen, W. A. S. Buxton: A comparison of input devices in elemental pointing and dragging tasks, Proceedings of the ACM CHI 1991 Conference on Human Factors in Computing Systems 1991, ISBN 978-0897913836, S. 161–166, doi:10.1145/108844.108868.
R Kerr: Movement time in an underwater environment. In: Journal of Motor Behavior. 5, Nr. 3, 1973, S. 175–178.
G Brogmus: Effects of age and sex on speed and accuracy of hand movements: And the refinements they suggest for Fitts' Law. In: Proceedings of the Human Factors Society Annual Meeting. 35, Nr. 3, 1991, S. 208–212.
B. C. M. Smits-Engelsman, P. H. Wilson, Y. Westenberg, J. Duysens: Fine motor deficiencies in children with developmental coordination disorder and learning disabilities: An underlying open-loop control deficit. In: Human movement science. 22, Nr. 4–5, 2003, S. 495–513.
T. O. Kvålseth: Effects of marijuana on human reaction time and motor control. In: Perceptual and motor skills. 45, Nr. 3, 1977, S. 935–939.
E. D. Graham, C. L. MacKenzie: Physical versus virtual pointing. In: Proceedings of the SIGCHI conference on Human factors in computing systems. 1996, S. 292–299.
Stuart K. Card, William K. English, Betty J. Burr: Evaluation of mouse, rate-controlled isometric joystick, step keys, and text keys for text selection on a CRT. In: Ergonomics. 21, Nr. 8, 1978, S. 601–613. doi:10.1080/00140137808931762.
Stuart Card. In: PARC. Archiviert vom Original am 11. Juli 2012.
Evan Graham: Pointing on a Computer Display. Simon Fraser University, 1996.
Drewes: Dissertation. In: Eye Gaze Tracking for Human Computer Interaction. LMU München: Fakultät für Mathematik, Informatik und Statistik, 2011.
I. Scott MacKenzie: Scott MacKenzie's home page. In: www.yorku.ca.
I. Scott MacKenzie: Fitts' law as a research and design tool in human–computer interaction. In: Human–Computer Interaction. 7, 1992, S. 91–139. doi:10.1207/s15327051hci0701_3.
R. William Soukoreff, Jian Zhao, Xiangshi Ren: The Entropy of a Rapid Aimed Movement: Fitts' Index of Difficulty versus Shannon's Entropy. In: Human Computer Interaction. 2011, S. 222–239.
A. T. Welford: Fundamentals of Skill. Methuen, 1968.
Paul M. Fitts, J. R. Peterson: Information capacity of discrete motor responses. In: Journal of Experimental Psychology. 67, Nr. 2, 1964, S. 103–112. doi:10.1037/h0045689.
R. Kopper, D. A. Bowman, M. G. Silva, R. P. MacMahan: A human motor behavior model for distal pointing tasks. In: International journal of human-computer studies. 68, Nr. 10, März, S. 603–615.
Garth Shoemaker, Takayuki Tsukitani, Yoshifumi Kitamura, Kellogg Booth: Two-Part Models Capture the Impact of Gain on Pointing Performance. In: ACM Transactions on Computer-Human Interaction. 19, Nr. 4, December 2012, S. 1–34. doi:10.1145/2395131.2395135.
J. Wobbrock, K Shinohara: The effects of task dimensionality, endpoint deviation, throughput calculation, and experiment design on pointing measures and models., Proceedings of the ACM Conference on Human Factors in Computing Systems 2011, ISBN 9781450302289, S. 1639–1648, doi:10.1145/1978942.1979181.
I. Scott MacKenzie, William A. S. Buxton: Extending Fitts' law to two-dimensional tasks, Proceedings of the ACM CHI 1992 Conference on Human Factors in Computing Systems 1992, ISBN 978-0897915137, S. 219–226, doi:10.1145/142750.142794.
H. Zhao: Fitt’s Law: Modeling Movement Time in HCI. In: Theories in Computer Human Interaction. 2002. Abgerufen am 8. Dezember 2019.
R. William Soukoreff, I. Scott MacKenzie: Towards a standard for pointing device evaluation, perspectives on 27 years of Fitts' law research in HCI. In: International Journal of Human-Computer Studies. 61, Nr. 6, 2004, S. 751–789. doi:10.1016/j.ijhcs.2004.09.001.
Shumin Zhai: On the Validity of Throughput as a Characteristic of Computer Input (pdf) Almaden Research Center, San Jose, California. 2002.
Byungjoo Lee, Antti Oulasvirta: Modelling Error Rates in Temporal Pointing, Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems (= CHI '16), ACM, New York, NY, USA 2016, ISBN 9781450333627, S. 1857–1868, doi:10.1145/2858036.2858143.
K Hale: Visualizing Fitts's Law. Particletree. 2007. Archiviert vom Original am 8. Dezember 2019. Abgerufen am 8. Dezember 2019.
H. Jensen: Giving You Fitts. Microsoft Developer. 2006. Archiviert vom Original am 8. Dezember 2019. Abgerufen am 8. Dezember 2019.
J Boritz, W. B. Cowan: Fitts's law studies of directional mouse movement. In: human performance. 1, Nr. 6, 1991. Abgerufen am 8. Dezember 2019.

Weblinks

Fitts' Law von CS Dept. NSF-Supported Education Infrastructure Project
Fitts’ Law: Modeling Movement Time in HCI
Bibliography of Fitts’ Law Research von I. Scott MacKenzie
Fitts' Law Software - Free Download von I. Scott MacKenzie
An Interactive Visualisation of Fitts's Law with JavaScript and D3 von Simon Wallner

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Fitts1954-1] Paul M. Fitts: The information capacity of the human motor system in controlling the amplitude of movement. In: Journal of Experimental Psychology. 47, Nr. 6, Juni 1954, S. 381–391. doi:10.1037/h0055392. PMID 13174710.

[2] Errol R. Hoffmann: A comparison of hand and foot movement times. In: Ergonomics. 34, Nr. 4, 1991, S. 397–406. doi:10.1080/00140139108967324. PMID 1860460.

[3] Marcelo Archajo Jose, Roleli Lopes: Human-computer interface controlled by the lip. In: IEEE Journal of Biomedical and Health Informatics. 19, Nr. 1, 2015, S. 302–308. doi:10.1109/JBHI.2014.2305103. PMID 25561451.

[4] R. H. Y. So, M. J. Griffin: Effects of target movement direction cue on head-tracking performance. In: Ergonomics. 43, Nr. 3, 2000, S. 360–376. doi:10.1080/001401300184468. PMID 10755659.

[5] I. Scott MacKenzie, A. Sellen, W. A. S. Buxton: A comparison of input devices in elemental pointing and dragging tasks, Proceedings of the ACM CHI 1991 Conference on Human Factors in Computing Systems 1991, ISBN 978-0897913836, S. 161–166, doi:10.1145/108844.108868.

[Kerr1973-6] R Kerr: Movement time in an underwater environment. In: Journal of Motor Behavior. 5, Nr. 3, 1973, S. 175–178.

[Brogmus1991-7] G Brogmus: Effects of age and sex on speed and accuracy of hand movements: And the refinements they suggest for Fitts' Law. In: Proceedings of the Human Factors Society Annual Meeting. 35, Nr. 3, 1991, S. 208–212.

[Smits2003-8] B. C. M. Smits-Engelsman, P. H. Wilson, Y. Westenberg, J. Duysens: Fine motor deficiencies in children with developmental coordination disorder and learning disabilities: An underlying open-loop control deficit. In: Human movement science. 22, Nr. 4–5, 2003, S. 495–513.

[Kvalseth1977-9] T. O. Kvålseth: Effects of marijuana on human reaction time and motor control. In: Perceptual and motor skills. 45, Nr. 3, 1977, S. 935–939.

[Graham-10] E. D. Graham, C. L. MacKenzie: Physical versus virtual pointing. In: Proceedings of the SIGCHI conference on Human factors in computing systems. 1996, S. 292–299.

[Card1978-11] Stuart K. Card, William K. English, Betty J. Burr: Evaluation of mouse, rate-controlled isometric joystick, step keys, and text keys for text selection on a CRT. In: Ergonomics. 21, Nr. 8, 1978, S. 601–613. doi:10.1080/00140137808931762.

[12] Stuart Card. In: PARC. Archiviert vom Original am 11. Juli 2012.

[Graham1996-13] Evan Graham: Pointing on a Computer Display. Simon Fraser University, 1996.

[Drewes2011-14] Drewes: Dissertation. In: Eye Gaze Tracking for Human Computer Interaction. LMU München: Fakultät für Mathematik, Informatik und Statistik, 2011.

[15] I. Scott MacKenzie: Scott MacKenzie's home page. In: www.yorku.ca.

[MacKenzie1992-16] I. Scott MacKenzie: Fitts' law as a research and design tool in human–computer interaction. In: Human–Computer Interaction. 7, 1992, S. 91–139. doi:10.1207/s15327051hci0701_3.

[Soukoreff2011-17] R. William Soukoreff, Jian Zhao, Xiangshi Ren: The Entropy of a Rapid Aimed Movement: Fitts' Index of Difficulty versus Shannon's Entropy. In: Human Computer Interaction. 2011, S. 222–239.

[Welford-18] A. T. Welford: Fundamentals of Skill. Methuen, 1968.

[Fitts1964-19] Paul M. Fitts, J. R. Peterson: Information capacity of discrete motor responses. In: Journal of Experimental Psychology. 67, Nr. 2, 1964, S. 103–112. doi:10.1037/h0045689.

[Kopper2010-20] R. Kopper, D. A. Bowman, M. G. Silva, R. P. MacMahan: A human motor behavior model for distal pointing tasks. In: International journal of human-computer studies. 68, Nr. 10, März, S. 603–615.

[Shoemaker_2012-21] Garth Shoemaker, Takayuki Tsukitani, Yoshifumi Kitamura, Kellogg Booth: Two-Part Models Capture the Impact of Gain on Pointing Performance. In: ACM Transactions on Computer-Human Interaction. 19, Nr. 4, December 2012, S. 1–34. doi:10.1145/2395131.2395135.

[Wobbrock2011-22] J. Wobbrock, K Shinohara: The effects of task dimensionality, endpoint deviation, throughput calculation, and experiment design on pointing measures and models., Proceedings of the ACM Conference on Human Factors in Computing Systems 2011, ISBN 9781450302289, S. 1639–1648, doi:10.1145/1978942.1979181.

[MacKenzie1992-2D-23] I. Scott MacKenzie, William A. S. Buxton: Extending Fitts' law to two-dimensional tasks, Proceedings of the ACM CHI 1992 Conference on Human Factors in Computing Systems 1992, ISBN 978-0897915137, S. 219–226, doi:10.1145/142750.142794.

[Zhao2002-24] H. Zhao: Fitt’s Law: Modeling Movement Time in HCI. In: Theories in Computer Human Interaction. 2002. Abgerufen am 8. Dezember 2019.

[Soukoreff2004-25] R. William Soukoreff, I. Scott MacKenzie: Towards a standard for pointing device evaluation, perspectives on 27 years of Fitts' law research in HCI. In: International Journal of Human-Computer Studies. 61, Nr. 6, 2004, S. 751–789. doi:10.1016/j.ijhcs.2004.09.001.

[Zhai2002-26] Shumin Zhai: On the Validity of Throughput as a Characteristic of Computer Input (pdf) Almaden Research Center, San Jose, California. 2002.

[27] Byungjoo Lee, Antti Oulasvirta: Modelling Error Rates in Temporal Pointing, Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems (= CHI '16), ACM, New York, NY, USA 2016, ISBN 9781450333627, S. 1857–1868, doi:10.1145/2858036.2858143.

[Hale2007-28] K Hale: Visualizing Fitts's Law. Particletree. 2007. Archiviert vom Original am 8. Dezember 2019. Abgerufen am 8. Dezember 2019.

[Jensen2002-29] H. Jensen: Giving You Fitts. Microsoft Developer. 2006. Archiviert vom Original am 8. Dezember 2019. Abgerufen am 8. Dezember 2019.

[Boritz1991-30] J Boritz, W. B. Cowan: Fitts's law studies of directional mouse movement. In: human performance. 1, Nr. 6, 1991. Abgerufen am 8. Dezember 2019.