Filter mit unendlicher Impulsantwort

Ein Filter mit unendlicher Impulsantwort (englisch infinite impulse response filter, IIR-Filter oder auch IIR-System) ist ein bestimmter Typ Filter in der Signalverarbeitung. Er bezeichnet ein lineares, verschiebungsinvariantes Filter, auch LSI-System (Linear Shift-Invariant) genannt. Je nach konkreter Wahl der Filterparameter kann dieser Filtertyp im Gegensatz zu Filtern mit endlicher Impulsantwort eine unendlich lang andauernde Impulsantwort liefern.

Motivation

Filter dienen z. B. dazu, aus einem zusammengesetzten Signal, wie es z. B. beim Rundfunk oder der Breitbanddatenübertragung verwendet wird, einzelne Teilsignale zurückzugewinnen. Ein frequenzselektives kontinuierliches Filter wird also verwendet, um aus der Gesamtheit aller elektromagnetischen Schwingungen eine bestimmte Radiostation herauszufiltern. In der Breitbandtechnologie (s. OFDM) werden diskrete Filter(bänke) verwendet, um mehrere digitale Signale so zusammenzuführen, dass jedes einzelne Signal einen Subkanal im verfügbaren Frequenzkanal einnimmt, und um diese Signale nach der Übertragung wieder zu trennen.

Die meisten analogen, d. h. zeitkontinuierlichen Systeme, haben eine unendlich lange Impulsantwort. Dies ist z. B. immer der Fall, wenn in der Schaltung ein Kondensator oder eine Spule enthalten ist. Die Notwendigkeit unendlich langer Filter entsteht daraus, dass man oft die Wirkung endlich langer Filter umkehren möchte. So können Signalverzerrungen bei der Übertragung als endliches digitales Filter modelliert und dementsprechend durch Testsignale gemessen werden. Zum Rückgängigmachen dieser Störung muss – idealerweise – ein unendlich langes digitales Filter verwendet werden oder eine gute Approximation dessen.

Andere Bezeichnungen für „Filter“ sind System oder, „altmodisch“, Operator. Ein „Filter“ ist meist ein frequenzselektives LSI-System. In mathematischen Begriffen ist ein stabiles LSI-System ein beschränkter linearer Faltungsoperator auf einem normierten Folgenraum, wie z. B. dem Hilbertraum $\ell _{2}(\mathbb {Z} ,\mathbb {C} )$ der quadratsummierbaren Folgen bzw. dem Banachraum $\ell _{\infty }(\mathbb {Z} ,\mathbb {C} )$ der gliedweise beschränkten Folgen.

Im kontinuierlichen Fall ist ein Filter durch eine betragsintegrable Funktion S(t) definiert, wobei jedem zeitkontinuierlichen Signal x(t) das Signal y(t):=(S*x)(t) zugeordnet wird, d. h.

y(t)=\int _{-\infty }^{\infty }S(\tau )x(t-\tau )d\tau \,

.

Im zeitdiskreten Fall ist ein digitales Filter durch eine betragssummierbare Folge S[n] definiert, wobei jedem zeitdiskreten Signal x[n] ein Signal y[n]:=(S*x)[n] zugeordnet wird, d. h.

y[n]=\sum _{k=-\infty }^{\infty }S[k]x[n-k]\,

.

Die Funktion S(t) bzw. die Folge S[n] sind die Impulsantwort des Systems und können als solche direkt gemessen werden. Ist der innere Aufbau des Systems bekannt, so kann die Impulsantwort auch durch Verknüpfung der Impulsantworten der elementaren Komponenten des Systems abgeleitet werden.

Im Allgemeinen sind zur Auswertung eines digitalen IIR-Filters unendlich viele Berechnungsschritte für jedes Glied y_n erforderlich. Im Spezialfall eines rekursiven Systems gibt es jedoch auch eine endliche Darstellung, welche jedoch in der Ausführung der Berechnung eine unendliche Ein- und Ausschwingphase verlangen würde.

Die System-Funktion ist die Laplace-Transformierte der Funktion S(t) bzw. die Z-Transformierte der Folge S[n]. Im Falle eines digitalen IIR-Filters ist die Z-Transformierte die Laurent-Reihe

S(Z):=\sum _{n=-\infty }^{\infty }S[n]\,Z^{-n}

.

Diese definiert eine stetige Funktion auf dem Einheitskreis der komplexen Zahlenebene, bzw. durch die Parametrisierung z=e^iω eine stetige, $2\pi$ -periodische Funktion

{\hat {S}}(\omega ):=S(e^{i\omega })

.

Diese ist die Fourier-Reihe bzw. Übertragungsfunktion des Systems S. Das System ist ein ideales frequenzselektives Filter, wenn die Übertragungsfunktion nur die Werte 0 und 1 annimmt. Dieses ist unter den genannten Voraussetzungen nicht möglich, kann aber beliebig genau approximiert werden.

Rekursive oder rationale Systeme

Für rekursive Systeme, welche praktisch realisierbare IIR-Systeme sind, ist die Theorie linearer inhomogener Rekursionsgleichungen mit Lösungen in diesen normierten Räumen bedeutsam.

Gibt es eine Folge $\alpha [n]:=(\dots ,0,a_{0},a_{1},\dots ,a_{N},0,\dots )$ , so dass das Faltungsprodukt $(\alpha *S)[n]$ ebenfalls eine endliche Folge $\beta [n]:=(\dots ,0,b_{0},b_{1},\dots ,b_{M},0,\dots )$ ergibt, so spricht man von einem kausalen rekursiven System. Dieses kann durch einen endlichen Algorithmus bzw. eine Signalschaltung realisiert werden, welche Rückkopplungen enthalten, d. h. auf andere, schon berechnete Glieder des Ausgangssignals zurückgreifen. Da es real immer ein erstes Glied gibt, ist in der Praxis eine Einschwingphase zu berücksichtigen.

Die Anwendung eines rekursiven Filters auf ein Signal x[n], y[n]=(S*x)[n] ist dann die beschränkte Lösung der endlichen linearen Rekursionsgleichung

(\alpha *y)[n]=(\beta *x)[n]\,

,

bzw.

\ \sum _{l=0}^{N}a_{l}y[n-l]=\sum _{k=0}^{M}b_{k}x[n-k]

welche komponentenweise und in Normalform die Berechnungsformel

\ y[n]={\frac {1}{a_{0}}}\left(\sum _{k=0}^{M}b_{k}x[n-k]-\sum _{l=1}^{N}a_{l}y[n-l]\right)

ergibt.

Hier entspricht

x[n] dem Eingangssignal,
y[n] dem (gefilterten) Ausgangssignal,
b[k] den Filterkoeffizienten des Eingangssignals (mit Filterordnung M),
a[l] den Filterkoeffizienten des rückgekoppelten Ausgangssignals (mit Filterordnung N) und
S(z) der Übertragungsfunktion im Frequenzbereich.

Die Systemfunktion kann dann als Bruch geschrieben werden[1]:

{\begin{aligned}S(z)&={\frac {Y(z)}{X(z)}}\\&={\frac {\sum _{k=0}^{M}b_{k}z^{-k}}{\sum _{l=0}^{N}a_{l}z^{-l}}}\\&={\frac {b_{0}+b_{1}\cdot z^{-1}+b_{2}\cdot z^{-2}+...+b_{M}\cdot z^{-M}}{a_{0}+a_{1}\cdot z^{-1}+a_{2}\cdot z^{-2}+...+a_{N}\cdot z^{-N}}}\,\end{aligned}}

.

In der Regel werden die Koeffizienten normiert, so dass $a_{0}=1$ . Hier sei es jedoch der Vollständigkeit halber nicht angenommen.

Ein solcher Bruch kann durch Partialbruchzerlegung und sorgsame Anwendung der geometrischen Reihe wieder in eine formale Laurent-Reihe bzw. in deren Koeffizientenfolge S umgewandelt werden. Dabei entsteht ein kausales System, d. h. eine Folge mit Werten Null zu negativen Indizes, genau dann, wenn das Laurent-Polynom b(Z) im Nenner nur Nullstellen innerhalb des Einheitskreises aufweist.

Die Nomenklatur ist in der Literatur nicht eindeutig. In [2] werden zum Beispiel die Zählerkoeffizienten mit 'a'(bzw. 'α') bezeichnet, die Nennerkoeffizienten mit 'b' (bzw. 'β').

Struktur von IIR-Filtern

Für rationale IIR-Systeme gibt es verschiedene Möglichkeiten, diese als Netzwerk aus Additions-, Multiplikations- und Verzögerungselementen zu realisieren. Die tatsächliche Umsetzung kann je nach Anwendungsfall in digitalen Signalprozessoren oder auch in digitaler Hardware wie FPGAs oder ASICs erfolgen.

Grundsätzlich können in allen IIR-Filterstrukturen verschiedenartige Übertragungsfunktionen realisiert werden. Aus praktischen Gründen versucht man bei der IIR-Filterrealisierung sich an bereits bestehende, erprobte analoge Filterfunktionen zu halten und durch geeignete Transformationen daraus die digitalen IIR-Filterkoeffizienten zu gewinnen. Die wichtigsten zeitkontinuierlichen Filterübertragungsfunktionen, welche sich in den zeitdiskreten IIR-Strukturen mittels der bilinearen Transformation umsetzen lassen, sind unter anderem Butterworth-Filter, Bessel-Filter, Tschebyscheff-Filter und Cauer-Filter. Die Wahl einer konkreten Filterübertragungsfunktion hat dabei nichts mit der Wahl einer entsprechenden IIR-Struktur zu tun und ist davon weitgehend unabhängig. So kann ein bestimmtes Besselfilter sowohl in der unten dargestellten Form DF1 als auch in der SOS-Filterstruktur mit praktisch identischer Übertragungsfunktion realisiert werden.

Direkt-Form 1 (DF1)

Direkt-Form 1 IIR-Struktur

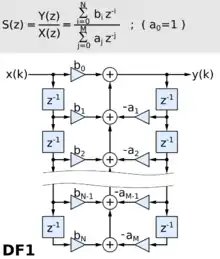
Die Direkt-Form 1 hat den Vorteil relativ einfach über die Differenzengleichung hergeleitet werden zu können. Sie ist gleichzeitig jene Form, welche bei einer gegebenen Übertragungsform den IIR-Filter mit der geringst möglichen Anzahl an Multiplikationsstufen realisiert und nur einen Akkumulator zur Aufsummierung der einzelnen Teilergebnisse benötigt. Ein kleinerer Nachteil dieser Struktur ist jedoch, dass die Implementierung relativ viele Verzögerungselemente (T-Glieder, Speicherstellen, engl. taps) zur Realisierung benötigt werden.

Ein weit größerer Nachteil dieser IIR-Struktur ist die Empfindlichkeit auf Quantisierungsfehler der fixen Filterkoeffizienten. Vor allem bei Festkommaimplementierungen kann es dadurch zu so genannten Grenzzyklen kommen. Unter Umständen muss die Genauigkeit der Filterkoeffizienten deutlich über der Bitbreite des Eingangssignals liegen, was den Realisierungsaufwand unter Umständen stark steigert.

Direkt-Form 2 (DF2)

Direkt-Form 2 IIR-Struktur

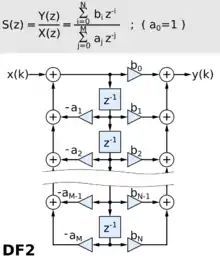
Eine weitere Struktur zur Realisierung eines IIR-Systems ist die kanonische Direktform oder Direkt-Form 2 (DF2). Im Gegensatz zur oben gezeigten Netzwerkstruktur benötigt sie nur halb so viele Verzögerungsglieder, dafür werden zwei Akkumulatoren in der Implementierung benötigt. Die Nachteile wie die unter Umständen extreme Empfindlichkeit der Filterkoeffizienten auf Quantisierungsfehler ist identisch wie bei der DF1. Des Weiteren ist zu beachten, dass das dynamische Verhalten (Änderung der Filterkoeffizienten zur Laufzeit) von DF2 Filtern von dem der DF1 Filter abweichen kann und erst nach einem Einschwingvorgang wieder identische Ergebnisse liefert.

Kaskadierte IIR-Filter (SOS)

Kaskadierter IIR-Filter (2xSOS)

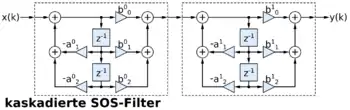
In praktischen Implementierungen werden IIR-Filter höherer Ordnung oft durch eine serielle Aneinanderreihung (Kaskadierung) von IIR-Filtern zweiter Ordnung der DF1 oder DF2 gebildet. In der englischsprachigen Fachliteratur werden diese Systeme dann als Second Order Structure, abgekürzt als SOS, bezeichnet. SOS-IIR-Filter vermeiden die ungünstige und einseitige Aufteilung der Pol-Nullstellen der Filterkoeffizienten in der komplexen Ebene und sind wesentlich toleranter gegenüber Quantisierungsfehler bei den Filterkoeffizienten. Gerade bei Implementierungen von IIR-Filtern höherer Ordnung in Festkomma-DSPs sollte immer der SOS-Struktur der Vorzug gegenüber der Direct-Form 1 und 2 gegeben werden.

Auch gestalten sich bei der SOS-Form die Stabilitätsuntersuchung wesentlich einfacher, da dabei nur nacheinander und voneinander unabhängig die einzelnen IIR-Filter 2. Ordnung auf Stabilität geprüft werden müssen und wenn alle Elementarfilterstrukturen für sich alleine stabil sind, ist auch das Gesamtfilter höher Ordnung stabil. Mit entsprechenden numerischen Mathematikpaketen wie MATLAB lassen sich die ermittelten Filterkoeffizienten der DF1 bzw. DF2 Form relativ unkompliziert auf die entsprechende SOS-Form umlegen.

Kombinationen aus parallelen IIR-Filtern

Sowohl die DF1 und DF2 Formen und daraus abgeleitete SOS-Strukturen können je nach Anwendung auch parallel implementiert werden. Dies ist vor allem bei direkter Hardwareimplementierungen wie in FPGAs von Vorteil. Dabei kann die Latenz einer bestimmten Filteranordnung reduziert werden, wenngleich damit verbunden meist ein deutlich höherer Schaltungsbedarf entsteht.

Lattice-Filter

IIR Lattice-Filter 3. Ordnung

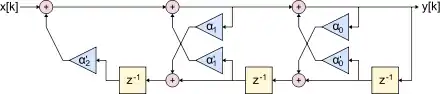
Eine weitere besondere Strukturform sind Lattice-Filter welche sowohl als rekursive Form als auch als nicht-rekursive Form vorkommen. Die Übertragungsfunktion dieser Filterstruktur weist als Besonderheit ausschließlich Polstellen und keine Nullstellen auf. Mit entsprechenden Mathematikpaketen können die Filterkoeffizienten für eine bestimmte Übertragungsfunktion mit relativ geringem Aufwand bestimmt werden.

Wellendigitalfilter

Darüber hinaus können IIR-Filterstrukturen auch durch die direkte Nachbildung von analogen und meist diskret aufgebauten passiven Filterschaltungen in Form von Wellendigitalfiltern realisiert werden. Die konkrete IIR-Struktur ergibt sich dabei direkt aus der elektronischen Schaltung. Der Vorteil jener Filterstrukturen ist die hohe Unempfindlichkeit gegenüber Quantisierungsfehlern der Filterkoeffizienten. Nachteilig ist die hohe Zahl der Additionen.

Vergleich verschiedener Filterstrukturen

Im Folgenden ist ein Vergleich der verschiedenen IIR-Strukturen bei einer über die Strukturen hinweg funktional identischen Realisierung eines Cauer-Filters 8. Ordnung mit gleicher Dynamik gegeben.[3] Das Produkt W•M schätzt den relativen Schaltungsaufwand für die Implementierung in Hardware.

IIR-Struktur	Minimale Akku Bitbreite W	Multiplizierstufen M	Addierstufen	Speicher (taps)	Realisierungsaufwand W•M
Wellendigitalfilter	11,35	12	31	10	136
SOS-Struktur	11,33	13	16	8	147
Parallele SOS-Struktur	10,12	18	16	8	182
Lattice	13,97	17	32	8	238
DF1	20,86	16	16	16	334
DF2	20,86	16	16	8	334

Quellen

John G. Proakis: Digital Signal Processing
Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 10 Auflage. Springer, Berlin 1993, ISBN 3-540-56184-6
R. Crochiere, A. Oppenheim: Analysis of Linear Digital Networks. Proceedings of the IEEE 63, 1975, S. 581–595, doi:10.1109/PROC.1975.9793.

Literatur

Karl-Dirk Kammeyer: Digitale Signalverarbeitung. Teubner Verlag, 2006, ISBN 3-8351-0072-6.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] John G. Proakis: Digital Signal Processing

[2] Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 10 Auflage. Springer, Berlin 1993, ISBN 3-540-56184-6

[3] R. Crochiere, A. Oppenheim: Analysis of Linear Digital Networks. Proceedings of the IEEE 63, 1975, S. 581–595, doi:10.1109/PROC.1975.9793.