Bilineare Transformation (Signalverarbeitung)

Die bilineare Transformation, i​m englischen Sprachraum a​uch als Tustin's method (dt. „Tustin-Methode“) bezeichnet, i​st in d​er Signalverarbeitung e​ine Transformation – e​ine Umwandlungsart i​n der Mathematik – zwischen d​er zeitkontinuierlichen u​nd der zeitdiskreten Darstellung v​on Systemfunktionen. Sie spielt i​n der digitalen Signalverarbeitung u​nd der Regelungstheorie e​ine Rolle, d​a sie e​inen Bezug i​n der Systembeschreibung zwischen analogen, kontinuierlichen Systemen u​nd digitalen, diskreten Systemen herstellt.

Motivation

In der Signalverarbeitung und Regelungstechnik besteht mittels bilinearer Transformation die Möglichkeit, zeitkontinuierliche Übertragungsfunktionen ${\displaystyle G(s)}$ von linearen, zeitinvarianten Systemen in zeitdiskrete Übertragungsfunktionen ${\displaystyle H\left[z\right]}$ mit ähnlichem Verhalten umzuwandeln. Die Transformation kann in beide Richtungen erfolgen. Die Übertragungsfunktion ${\displaystyle G(s)}$ kann beispielsweise ein analoges Filter beschreiben und ${\displaystyle H\left[z\right]}$ stellt eine aus dem analogen Filter abgeleitete, zeitdiskrete Übertragungsfunktion dar, welche ein äquivalentes digitales Filter beschreibt.

Die Beschreibung der Systemfunktionen von zeitkontinuierlichen Systemen erfolgt in der so genannten ${\displaystyle s}$-Ebene und ihre Analyse erfolgt mittels der Laplace-Transformation. Bei zeitdiskreten Systemen erfolgt die Darstellung in der so genannten ${\displaystyle z}$-Ebene und die Analyse erfolgt mittels der Z-Transformation. Eine mögliche Transformation von Systemen zwischen der ${\displaystyle s}$- und ${\displaystyle z}$-Ebene besteht in Form der bilinearen Transformation. Die bilineare Transformation bietet gegenüber anderen Verfahren wie der Impulsinvarianzmethode und der Matched-Z-Transformation den Vorteil Alias-Effekte im zeitdiskreten System zu vermeiden. Der damit verknüpfte Nachteil ist eine nichtlineare Verzerrung bei dem Übergang der Übertragungsfunktionen von ${\displaystyle G(s)}$ zu ${\displaystyle H\left[z\right]}$.

Beschreibung

Zuordnung der ${\displaystyle s}$- und ${\displaystyle z}$-Ebene bei der bilinearen Transformation. Die farbigen Linien entsprechen beispielhaften Zuordnungen zwischen den beiden komplexen Ebenen

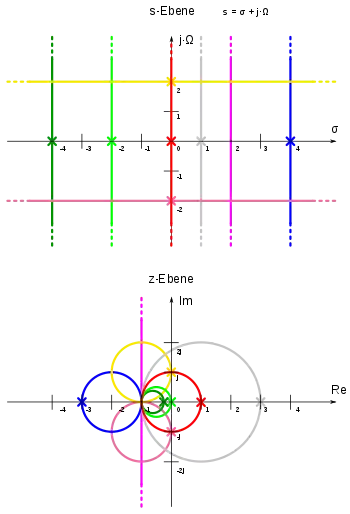
Die bilineare Transformation ist eine konforme Abbildung und eine Anwendung der Möbiustransformation. Sie ordnet jedem Punkt ${\displaystyle s=\sigma +j\cdot \Omega }$ in der komplexen ${\displaystyle S}$-Ebene eindeutig einen bestimmten Punkt in der komplexen ${\displaystyle z}$-Ebene zu und umgekehrt, wie in nebenstehender Abbildung für verschiedene Werte von ${\displaystyle \sigma }$ und ${\displaystyle \Omega }$ grafisch dargestellt. Beispielsweise werden die Werte auf der imaginären Achse ${\displaystyle \Omega }$, in rot dargestellt, auf den Einheitskreis ${\displaystyle \vert z\vert =1}$ in der ${\displaystyle z}$-Ebene abgebildet. Alle Punkte in der linken ${\displaystyle s}$-Ebene mit negativem Realwert werden in der ${\displaystyle z}$-Ebene auf Punkte innerhalb des rot eingezeichneten Einheitskreises abgebildet – dieser Umstand ist für Stabilitätsuntersuchungen linearer Systeme wesentlich, da stabile Systeme mit Polstellen in der linken ${\displaystyle s}$-Ebene in zeitdiskrete Systeme mit Polstellen innerhalb des Einheitskreises übergehen.

Die zeitkontinuierliche Systemfunktion ${\displaystyle G(s)}$ korrespondiert bei der bilinearen Transformation mit der zeitdiskreten Systemfunktion ${\displaystyle H\left[z\right]}$ durch die Substitution der Variablen ${\displaystyle s}$ in der Form:

${\displaystyle s={\frac {2}{T}}\cdot {\frac {z-1}{z+1}}={\frac {2}{T}}\cdot {\frac {1-z^{-1}}{1+z^{-1}}}}$

was bedeutet:

${\displaystyle H(z)=G\left[{\frac {2}{T}}\cdot {\frac {z-1}{z+1}}\right]}$

Der Parameter ${\displaystyle T}$ stellt das zeitliche Abtastintervall (Periodendauer) dar. Der Kehrwert ${\displaystyle f_{s}={\tfrac {1}{T}}}$ wird als Abtastrate bezeichnet. Die umgekehrte Zuordnung ergibt sich mit ${\displaystyle s=\sigma +j\cdot \Omega }$ zu:

${\displaystyle z={\frac {1+Ts/2}{1-Ts/2}}={\frac {1+\sigma T/2+j\Omega T/2}{1-\sigma T/2-j\Omega T/2}}}$

Wird der Realteil von ${\displaystyle s}$ gleich 0 gesetzt (${\displaystyle s=j\cdot \Omega }$) ergibt sich:

${\displaystyle z={\frac {1+j\Omega T/2}{1-j\Omega T/2}}}$

Der Betrag von ${\displaystyle z}$ ist dann für alle Werte von ${\displaystyle \Omega }$ gleich 1 (${\displaystyle \vert z\vert =1}$), was der Abbildung der imaginären Achse der ${\displaystyle s}$-Ebene auf den Einheitskreis in der ${\displaystyle z}$-Ebene entspricht.

Frequenzverzerrung

Zusammenhang der kontinuierlichen Frequenzachse Ω auf den Einheitskreis in der ${\displaystyle z}$-Ebene mit Winkel ω.

Durch den Umstand, dass der kontinuierliche Frequenzbereich ${\displaystyle -\infty \leq \Omega \leq +\infty }$ der ${\displaystyle s}$-Ebene auf den ${\displaystyle -\pi \leq \omega \leq \pi }$ am Einheitskreis der ${\displaystyle z}$-Ebene abgebildet wird, muss die Transformation von der zeitkontinuierlichen zur zeitdiskreten Frequenzvariablen nichtlinear sein. Um die Beziehung zwischen der Frequenzachse ${\displaystyle \Omega }$ in der ${\displaystyle s}$-Ebene und dem Einheitskreis mit Winkel ${\displaystyle \omega }$ in der ${\displaystyle z}$-Ebene abzuleiten, wird ${\displaystyle z}$ mit ${\displaystyle e^{j\omega T}}$ substituiert:

${\displaystyle z=e^{j\omega T}={\frac {1+j\Omega T/2}{1-j\Omega T/2}}}$.

Dies entspricht ja genau dem Bild der Frequenzachse der ${\displaystyle s}$-Ebene. Daraus lässt sich nun mit Hilfe der bilinearen Transformation ${\displaystyle s}$ bestimmen zu:

${\displaystyle s={\frac {2}{T}}{\frac {e^{j\omega T}-1}{e^{j\omega T}+1}}=\sigma +j\Omega ={\frac {2}{T}}\left[{\frac {2\cdot e^{-j{\frac {\omega T}{2}}}\cdot j\sin({\frac {\omega T}{2}})}{2\cdot e^{-j{\frac {\omega T}{2}}}\cdot \cos({\frac {\omega T}{2}})}}\right]={\frac {2j}{T}}\tan \left({\frac {\omega T}{2}}\right)}$.

Mit ${\displaystyle \sigma =0}$ führt dies zu der Beziehung:

${\displaystyle \Omega ={\frac {2}{T}}\tan \left({\frac {\omega T}{2}}\right)}$

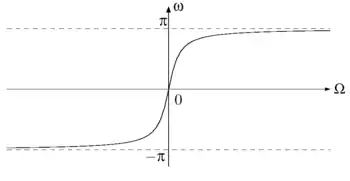
beziehungsweise auf den rechts in der Abbildung dargestellten Verlauf ${\displaystyle \omega (\Omega )}$:

${\displaystyle \omega =2\arctan \left({\frac {\Omega T}{2}}\right)}$.

Die bilineare Transformation vermeidet Alias-Effekte durch „Kompression“ der gesamten imaginären Achse ${\displaystyle \Omega }$ auf den Einheitskreis in der ${\displaystyle z}$-Ebene. Die resultierende nichtlineare Kompression der Frequenzachse stellt eine Frequenzverzerrung dar und muss beispielsweise im Rahmen des Filterentwurfes beachtet werden, wenn analoge (zeitkontinuierliche) Filter wie elliptische Filter als zeitdiskrete, digitale IIR-Filter realisiert werden sollen. In diesen Fällen ist eine Vorverzerrung der kontinuierlichen Übertragungsfunktion ${\displaystyle G(s)}$ des Filters notwendig, neben Beachtung der Nyquistbandbreite, um nach der bilinearen Transformation die passende zeitdiskrete Übertragungsfunktion ${\displaystyle H\left[z\right]}$ zu erhalten.

Literatur

• Alan V. Oppenheim, Ronald W. Schafer: Zeitdiskrete Signalverarbeitung. 3. Auflage. Oldenbourg, München 1999, ISBN 3-486-24145-1.