Fermi-Resonanz

Die Fermi-Resonanz (nach Enrico Fermi) ist ein physikalisches Phänomen der Molekülspektroskopie, das in Infrarot- und Raman-Spektren beobachtet werden kann. Dabei kommt es bei Schwingungen mit zufälliger Entartung zu einer Resonanzaufspaltung der Schwingungsbanden.

Beschreibung

Moleküle werden durch Absorption von Infrarot-Strahlung in einen angeregten Schwingungszustand versetzt. Für die Untersuchung dieses Absorptionsverhalten häufig in Form eines Intensitätsspektrums dargestellt, beispielsweise die Absorption gegenüber der Strahlungsenergie, die in der Molekülspektroskopie häufig als Wellenzahl (übliche Einheit: 1/cm) angegeben wird.

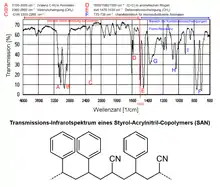
Infrarotspektrum eines Styrol-Acrylnitril-Copolymers (SAN)

Das IR-Spektrum eines organischen Moleküls (vgl. Bild) kann grob in zwei große Bereiche aufgeteilt werden. Im Wellenzahlenbereich unterhalb von 1500 cm⁻¹ befinden sich allgemein die energieärmeren Deformationsschwingungen. Im Bereich größer 1500 cm⁻¹ befinden sich in der Regel die Valenzschwingungen der funktionellen Gruppen sowie deren Ober- und Kombinationsschwingungen (Mehrfache bzw. Kombinationen aus zwei oder mehr Normalschwingungen). Gleichartige Schwingungen mit der gleichen Energie nennt man entartet.

Idealisiertes Auftreten einer Normal- und Oberschwingung vor und nach der Fermi-Resonanz. Unter den idealisierten Spektren ist das zugehörige idealisierte Energieniveauschema dargestellt.

Es ist möglich, dass Normal-, Ober- und Kombinationsschwingungen zufällig (näherungsweise) gleiche Energien besitzen, man nennt diese Schwingungen dann zufällig entartet.[1] Dabei kommt es zu einer Schwingungskopplung (Fermi-Resonanz) bei der eine Schwingung Energie von der anderen bezieht. Da hierbei die Energie der Oberschwingung zunimmt und die Energie der Normalschwingung abnimmt, kommt es zu einer ungewöhnlichen Überhöhung der Oberschwingung. Die Folge ist eine energetische Aufspaltung der zufällig entarteten Schwingungsbanden in zwei Banden ähnlicher Intensität (Fermi-Dublett).[1] Die Intensität entspricht nun der einer Grundschwingung, mit der sie leicht verwechselt werden kann.

Die Frequenzverschiebung der einzelnen Schwingungen entspricht dem anderer gekoppelten Schwingungen, das heißt, die frequenzhöhere Schwingung verschiebt sich nach einer noch höheren Frequenz und die frequenztiefere zu einer noch tieferen Frequenz.[2] Bei der Spektrenanalyse ist zu beachten, dass wenn eine Oberschwingung die frequenzhöhere Schwingung ist, sich die Frequenz in einen Bereich oberhalb des aus der Grundfrequenz berechneten Werts verschieben kann. Damit ist die Bedingung, dass eine Oberschwingung immer einen etwas niedrigeren Wert als berechnet besitzt, nicht mehr gegeben.

Die Fermi-Resonanz tritt jedoch nicht in allen Fällen auf, bei denen eine Ober- oder Kombinationsschwingung eine ähnliche Energie wie eine Grundschwingung aufweist. Eine wichtige Randbedingung ist, dass die Ober- oder Kombinationsschwingung der gleichen Symmetrierasse (Mulliken-Symbole) wie die Grundschwingung entsprechen.[2]

Beispiele

Beispiele für die Fermi-Resonanz sind die Resonanzaufspaltungen:

der symmetrischen Valenzschwingung ν₁ (≈ 1340 cm⁻¹) und der ersten Oberschwingung der Deformationsschwingung ν₃ des Kohlenstoffdioxid (CO₂) bei 2 × 667 cm⁻¹ = 1334 cm⁻¹, die in zwei um etwa ±50 cm⁻¹ verschobene Banden bei 1286 cm⁻¹ und 1389 cm⁻¹ resultieren[1][2] (wegen der Symmetrieverhältnisse nur im Raman-Spektrum)
der ersten Oberschwingung der Deformationsschwingung von Chlorcyan (ClCN) (2 × 378 cm⁻¹ → 753 cm⁻¹) der C-Cl-Valenzschwingung bei 744 cm⁻¹, die in zwei Banden bei 784 cm⁻¹ und 714 cm⁻¹ resultieren[2]

Rückrechnung

Mit Hilfe einer Näherungsformel[2] und den Bandenpositionen des Fermi-Dubletts ist es möglich die Wellenzahlen der „ungestörten“ Schwingungen zu bestimmen.

{\tilde {\nu }}_{\text{korr.}}={\frac {{\tilde {\nu }}_{1}+{\tilde {\nu }}_{2}}{2}}\pm {\frac {{\tilde {\nu }}_{1}-{\tilde {\nu }}_{2}}{2}}\cdot {\frac {s-1}{s+1}}

Für den oben erwähnten Fall des Chlorcyan erhält man für einen Wert von s ≈ 1,45 die korrigierten Werte von 753 cm⁻¹ und 744 cm⁻¹.

Literatur

Dana W. Mayo, Foil A. Miller, R. W. Hannah: Course notes on the interpretation of infrared and Raman spectra. Wiley-Interscience, Hoboken, N.J. 2004, ISBN 0-471-24823-1.

Einzelnachweise

Helmut Günzler, Hans-Ulrich Gremlich: IR-Spektroskopie. John Wiley & Sons, 2012, ISBN 978-3-527-66287-6.
Johann Weidlein , Ulrich Müller , Kurt Dehnicke: Schwingungsspektroskopie : Eine Einführung. 2., überarb. Auflage. Thieme, Stuttgart 1988, ISBN 3-13-625102-4, S. 37.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[günzler-1] Helmut Günzler, Hans-Ulrich Gremlich: IR-Spektroskopie. John Wiley & Sons, 2012, ISBN 978-3-527-66287-6.

[weidlein-2] Johann Weidlein , Ulrich Müller , Kurt Dehnicke: Schwingungsspektroskopie : Eine Einführung. 2., überarb. Auflage. Thieme, Stuttgart 1988, ISBN 3-13-625102-4, S. 37.