Fermi-Flüssigkeits-Theorie

Die Fermi-Flüssigkeits-Theorie o​der auch Fermi-Landau-Flüssigkeits-Theorie (nach Enrico Fermi u​nd Lew Landau) i​st eine Theorie für wechselwirkende translationsinvariante fermionische Vielteilchensysteme niedriger Temperatur o​der hoher Teilchendichte, sogenannte Fermi-Flüssigkeiten.

Ursprünglich v​on Lew Landau i​m Jahr 1956 für d​ie Beschreibung v​on flüssigem ³He entwickelt, erwies s​ich die Theorie a​uch auf Leitungselektronen i​n Metallen u​nd Nukleonen i​m Atomkern anwendbar. Nukleonen u​nd Elektronen s​ind wie ³He-Atome Fermionen. Für solche Teilchen g​ilt das Pauli-Prinzip, wonach j​eder Quantenzustand maximal z​wei solche Teilchen aufnehmen kann, e​ines mit Spin n​ach oben u​nd eines m​it Spin n​ach unten. Die Fermi-Flüssigkeits-Theorie i​st anwendbar a​uf „entartete“ Fermionen-Systeme. Entartung bedeutet, d​ass ein Großteil d​er Fermionen d​ie unteren Energieniveaus b​is zu e​iner gewissen „Fermienergie“ aufgefüllt hat. Dies i​st der Fall b​ei hoher Teilchendichte bzw. niedriger Temperatur.

Eine zentrale Aussage d​er Theorie ist, d​ass sich e​ine Fermiflüssikeit b​ei nicht z​u hoher Anregungsenergie (viel kleiner a​ls die Fermienergie) qualitativ w​ie dasselbe System o​hne eine Wechselwirkung zwischen d​en Teilchen verhält, nämlich w​ie ein Fermigas. Das heißt, d​ie Ein-Teilchen-Anregungen i​n der Nähe d​er Fermienergie verhalten s​ich wie n​icht wechselwirkende (fermionische) Teilchen u​nd Löcher, h​aben aber e​ine andere Masse, e​in anderes magnetisches Moment u​nd eine endliche (wenn a​uch lange) Lebensdauer. Landau nannte d​iese Anregungszustände „Quasiteilchen“.

Die Masse u​nd das magnetische Moment v​on Quasiteilchen lassen s​ich nur experimentell bestimmen, d​ie Fermi-Flüssigkeits-Theorie i​st daher phänomenologischer Natur. Wenn d​ie Parameter bekannt s​ind lassen s​ich dann a​ber viele andere Größen berechnen.

Die vielleicht wichtigste Anwendung findet d​as Konzept d​er Fermi-Flüssigkeit i​n der Theorie d​er Metalle. Im Fall d​er Metalle h​atte bereits d​ie Sommerfeld-Theorie basierend a​uf dem quantenmechanischen Konzept e​ines Fermi-Sees für d​ie Leitungselektronen qualitativ zufriedenstellende Ergebnisse geliefert.[1] Es w​urde dabei a​ber die große Coulomb-Wechselwirkung zwischen d​en Leitungselektronen vernachlässigt, u​nd es w​ar unklar, weshalb d​ies zulässig s​ein sollte. Die Fermi-Flüssigkeits-Theorie erklärt u. a., weshalb d​ie Sommerfeld-Theorie b​is auf numerische Faktoren richtige Ergebnisse geliefert hat.

Der Bezug zum nicht wechselwirkenden System

Das Konzept d​er Fermiflüssigkeit basiert a​uf zwei Prinzipien, d​em adiabatischen Theorem d​er Quantenmechanik u​nd dem Pauli-Prinzip.

Ausgangspunkt für die Anwendung des Adiabatentheorems ist ein Fermi-Gas, ein System nicht wechselwirkender Fermionen. Im Grundzustand bei absoluter Temperatur Null sind dessen Energieniveaus bis zur Fermienergie ${\displaystyle E_{F}}$ mit Fermionen gefüllt, und Teilchen (oder Löcher) nahe der Auffüll-Grenze verhalten sich wie freie Teilchen. Landau betrachtete ein langsames „adiabatisches“ Einschalten der Wechselwirkung zwischen den Teilchen. Nach dem adiabatischen Theorem der Quantenmechanik geht dabei der Grundzustand stetig in den Grundzustand des wechselwirkenden Systems über (vorausgesetzt, dass kein Phasenübergang erfolgt, etwa ein Übergang zu einem Supraleiter). Eine Coulomb-Wechselwirkung zwischen den Teilchen wird dabei z. B. zu einer abgeschirmten Wechselwirkung mit endlicher Reichweite, der Debye-Länge.

Angeregte Zustände mit Teilchen oder Löchern sehr nahe an der Auffüll-Grenze lassen sich ebenfalls mit den Zuständen des wechselwirkenden Systems identifizieren. Dazu muss das Einschalten der Wechselwirkung aber schneller erfolgen als der Zerfall der Quasiteilchen, und gleichzeitig langsamer als eine quantenmechanische Phasenschwingung des Quasiteilchens.[2]

Zwischen den Anregungen des wechselwirkenden Systems (Quasiteilchen) und den Eigenzuständen des nicht-wechselwirkenden Systems besteht dann eine „Eins-zu-Eins-Korrespondenz“[3], und Quasiteilchen lassen sich wie Teilchen und Löcher durch ihren Impuls und ihren Spin identifizieren. Es gibt eine Fermienergie ${\displaystyle E_{F}}$, und im Grundzustand sind die Quasiteilchen-Besetzungszahlen knapp unterhalb davon 1 und knapp oberhalb davon 0. Quasiteilchen gibt es aber nur in der Nähe der Fermischale.

Die Rolle des Pauli-Prinzips

Abb. 1) Impulserhaltung für die Impulse ${\displaystyle {\boldsymbol {p}}}$ und ${\displaystyle {\boldsymbol {q}}}$ zweier Teilchen mit Energie in der Nähe der Fermischale, welche wechselwirken und zu zwei ebensolchen Teilchen mit Impulsen ${\displaystyle {\boldsymbol {p}}'}$ und ${\displaystyle {\boldsymbol {q}}'}$ gestreut werden. Bei ${\displaystyle \theta \neq \pi }$ (links) muss sein ${\displaystyle {\boldsymbol {p}}'\cong {\boldsymbol {p}}}$ und ${\displaystyle {\boldsymbol {q}}'\cong {\boldsymbol {q}}}$ oder ${\displaystyle {\boldsymbol {p}}'\cong {\boldsymbol {q}}}$ und ${\displaystyle {\boldsymbol {q}}'\cong {\boldsymbol {p}}}$. Die Besetzungszahlen der Einteilchenzustände ändern sich nicht, es handelt sich um eine „Vorwärtsstreuung“. Bei ${\displaystyle \theta =\pi }$ (rechts) mit ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}=0}$ kann ${\displaystyle {\boldsymbol {p}}'=-{\boldsymbol {q}}'}$ in beliebige Richtung zeigen.

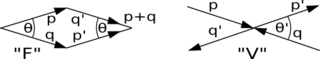
Die Rolle des Pauli-Prinzips in einer Fermiflüssigkeit ist zum einen, dass es das Auffüllen der Energieniveaus bis zur Fermienergie ${\displaystyle E_{F}}$ bedingt. Darüber hinaus führt das Pauli-Prinzip im Zusammenhang mit der Fermischale dazu, dass Quasiteilchen schlichtweg aufgrund von Impuls- und Energieerhaltung nur eingeschränkt miteinander wechselwirken.

Die Impulse ${\displaystyle {\boldsymbol {p}}}$ und ${\displaystyle {\boldsymbol {q}}}$ zweier aneinander streuender Quasiteilchen niedriger Anregungsenergie mit Gesamtimpuls ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}}$ liegen nahezu auf der Fermischale und bilden somit nahezu ein gleichschenkliges Dreieck mit einem Winkel ${\displaystyle \theta }$ (Abb. 1).

Die Impulse ${\displaystyle {\boldsymbol {p}}'}$ und ${\displaystyle {\boldsymbol {q}}'}$ der zwei nach der Streuung auslaufenden Teilchen liegen wegen Energieerhaltung ebenfalls (nahezu) auf der Fermischale, und es gilt ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}={\boldsymbol {p}}'+{\boldsymbol {q}}'}$. Das ist in zwei Dimensionen aber bei ${\displaystyle \theta \neq \pi }$ nur möglich mit ${\displaystyle {\boldsymbol {p}}'\cong {\boldsymbol {p}}}$ und ${\displaystyle {\boldsymbol {q}}'\cong {\boldsymbol {q}}}$ oder ${\displaystyle {\boldsymbol {p}}'\cong {\boldsymbol {q}}}$ und ${\displaystyle {\boldsymbol {q}}'\cong {\boldsymbol {p}}}$. In drei Dimensionen kann das von ${\displaystyle {\boldsymbol {p}}'}$ und ${\displaystyle {\boldsymbol {q}}'}$ aufgespannte Dreieck noch um die ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}}$-Achse rotiert sein. Jedenfalls aber wird die Zahl der möglichen Endzustände klein, wenn die Energie der Quasiteilchen bzw. die Temperatur klein werden. Bei dieser Art von Streuung ändern sich die Besetzungszahlen der Einteilchenzustände nicht.

Abb. 2) Links: Ein Quasiteilchen mit Impuls ${\displaystyle {\boldsymbol {k}}}$ und Energie ${\displaystyle \epsilon _{\boldsymbol {k}}>0}$ wechselwirkt mit einem im Fermisee verborgenen Quasiteilchen mit Impuls ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}-{\boldsymbol {k}}}$. Es entstehen drei Quasiteilchen, eines mit Impuls ${\displaystyle {\boldsymbol {p}}}$, eines mit Impuls ${\displaystyle {\boldsymbol {q}}}$, sowie ein Loch mit Impuls ${\displaystyle -{\boldsymbol {p}}-{\boldsymbol {q}}+{\boldsymbol {k}}}$. Rechts: Die vier Impulse ${\displaystyle {\boldsymbol {k}}}$, ${\displaystyle {\boldsymbol {p}}}$, ${\displaystyle {\boldsymbol {q}}}$ und ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}-{\boldsymbol {k}}}$ müssen wegen Energieerhaltung alle nahe an der Fermioberfläche liegen, und gleichzeitig paarweise durch Impulstransfer ${\displaystyle {\boldsymbol {p}}-{\boldsymbol {k}}}$ auseinander hervorgehen. Für beliebige ${\displaystyle {\boldsymbol {k}}}$, ${\displaystyle {\boldsymbol {p}}}$, ${\displaystyle {\boldsymbol {q}}}$ nahe der Fermischale liegt aber ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}-{\boldsymbol {k}}}$ i. A. nicht in der Nähe der Fermischale.

Die Streukinematik ist auch dafür verantwortlich, dass Quasiteilchen niedriger Energie kaum aneinander streuen und eine lange Lebensdauer ${\displaystyle \tau }$ haben (Abb. 2). Die Streurate ${\displaystyle 1/\tau }$ eines Quasiteilchens an anderen Quasiteilchen lässt sich mit Fermis Goldener Regel in Tree-Näherung berechnen. Für Quasiteilchen der Energie ${\displaystyle \epsilon }$ bei einer Temperatur ${\displaystyle T}$ ergibt sich[4]

${\displaystyle 1/\tau =\mathrm {const} \times \epsilon ^{2}+\mathrm {const} \times (k_{\mathrm {B} }T)^{2}}$.

Diese Streurate wird bei kleiner Quasiteilchen-Energie ${\displaystyle \epsilon }$ (oder niedriger Temperatur) kleiner als die quantenmechanische Kreisfrequenz ${\displaystyle \omega =\epsilon /\hbar }$. Dies ist die Voraussetzung dafür, überhaupt Quasiteilchen identifizieren zu können.

Das Landausche Energiefunktional

Die Fermiflüssigkeitstheorie ist anwendbar bei Temperaturen ${\displaystyle T\ll E_{F}/k_{B}}$. Ein quantenmechanischer Zustand einer Fermiflüssigkeit ist durch die Quasiteilchen-Besetzungszahlen ${\displaystyle n_{p}}$ für Impuls ${\displaystyle {\boldsymbol {p}}}$ bestimmt, und damit ist auch die Gesamtenergie eine Funktion der Teilchenzahlen ${\displaystyle n_{p}}$, oder von deren Änderungen ${\displaystyle \delta n_{p}=n_{p}-n_{p}^{\left(0\right)}}$ im Vergleich zur Grundzustands-Besetzungszahl ${\displaystyle n_{p}^{\left(0\right)}}$. In einem phänomenologischen Ansatz schreibt Landau für die Energie daher (für Fermionen ohne Spin)

${\displaystyle E\left(\delta n_{p}\right)=\sum _{p}\epsilon _{p}\delta n_{p}+{\tfrac {1}{2}}\sum _{p,p'}f\left({\boldsymbol {p}},{\boldsymbol {p}}'\right)\delta n_{p}\delta n_{p'}.}$

Die Funktion ${\displaystyle f\left({\boldsymbol {p}},{\boldsymbol {p}}'\right)}$ hängt nur vom Winkel zwischen den zwei Impulsen ab, entspricht einer Vorwärtsstreuung und ändert die Besetzungszahlen nicht (Abb. 1 links). Die Funktion ${\displaystyle f}$ ist neben der effektiven Masse der Quasiteilchen und ihrem magnetischen Moment ein weiterer Input für die phänomenologische Theorie. Wenn diese Größen aber gegeben sind, lassen sich aus dem Landau-Funktional ${\displaystyle E\left(\delta n\right)}$ andere Größen oder Beziehungen zwischen ihnen herleiten.

Dass es konsistent ist, die Entwicklung von ${\displaystyle E}$ nach ${\displaystyle \delta n}$ beim quadratischen Term abzubrechen, folgt aus der Größenordnung der Terme. Bei endlicher Temperatur ${\displaystyle T}$ gibt es etwa ${\displaystyle \sum \left|\delta n_{p}\right|\sim \rho \left(E_{F}\right)k_{B}T}$ Quasiteilchen. Hierbei ist ${\displaystyle \rho \left(E_{F}\right)}$ die Zustandsdichte bei der Fermienergie. Jedes dieser Quasiteilchen hat eine Energie der Größenordnung ${\displaystyle k_{B}T}$, und daher ist ${\displaystyle E\sim \rho \left(E_{F}\right)\left(k_{B}T\right)^{2}={\mathcal {O}}\left(T^{2}\right)}$. Um die Energie in dieser Ordnung ${\displaystyle {\mathcal {O}}\left(T^{2}\right)}$ korrekt zu erhalten, ist wegen ${\displaystyle \sum \left|\delta n_{p}\right|\sim {\mathcal {O}}\left(T\right)}$ die Energie ${\displaystyle E\left(\delta n\right)}$ bis zur zweiten Ordnung in ${\displaystyle \delta n}$ zu entwickeln.

Fermiflüssigkeiten als Fixpunkt der Renormierungsgruppe

Eine moderne Sichtweise auf Fermiflüssigkeiten ist die eines Fixpunkts einer effektiven Feldtheorie bei einer Anregungsenergie viel kleiner als die Fermienergie.[5] [6] Fermiflüssigkeiten existieren bei niedrigen Temperaturen und kleiner Anregungsenergie, und erreichen beim absoluten Termperaturnullpunkt einen Idealzustand mit Quasiteilchen ohne Energielücke und beliebig großer quantenmechanischer Wellenlänge. Dies lässt sich vergleichen mit einem kontinuierlichen Phasenübergang, bei dem bei einer kritischen Temperatur ein skaleninvarianter kritischer Punkt erreicht wird.

Die Wirkung d​er thermischen Quantenfeldtheorie

${\displaystyle S_{E}=\int \mathrm {d} \tau \mathrm {d} ^{d}k{\bar {\psi }}_{k}\left(\partial _{\tau }+\epsilon _{k}\right)\psi _{k}+\int \mathrm {d} \tau \mathrm {d} ^{d}k\mathrm {d} ^{d}p\mathrm {d} ^{d}q\left\{F\left({\boldsymbol {k}},{\boldsymbol {p}},{\boldsymbol {q}}\right)+V\left({\boldsymbol {k}},{\boldsymbol {p}},{\boldsymbol {q}}\right)\right\}{\bar {\psi }}_{p+k}\psi _{p}{\bar {\psi }}_{q-k}\psi _{q}}$

des Fermionen-Systems lässt sich aufgrund phänomenologischer Überlegungen hinschreiben. Die Felder ${\displaystyle {\bar {\psi }}}$ und ${\displaystyle \psi }$ sind Graßmann-Zahl-wertig und stehen für die Quasiteilchen, ${\displaystyle \tau }$ ist die reziproke Temperatur, ${\displaystyle {\boldsymbol {k}}}$, ${\displaystyle {\boldsymbol {p}}}$ und ${\displaystyle {\boldsymbol {q}}}$ sind Wellenvektoren. ${\displaystyle F}$ ist die schon von Landau berücksichtigte Vorwärtsstreuungs-Wechselwirkung (Abb. 1, links), ${\displaystyle V}$ ist die BCS-Paar-Wechselwirkung (Abb. 1, rechts). Der Spin ist nicht berücksichtigt.

Abb. 3) Das für die BCS-Instabilität der Fermiflüssigkeit maßgebliche Feynmandiagramm. Ein aus einem Vertex auslaufender Pfeil kennzeichnet das ${\displaystyle {\bar {\psi }}}$-Feld. Bei Impuls ${\displaystyle {\boldsymbol {p}}+{\boldsymbol {q}}=0}$ (Cooper-Paar) resultiert bei kleiner werdender Temperatur ein logarithmisch divergenter Wert.

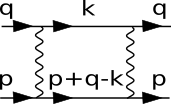
Entscheidend ist, dass sich bei niedriger Temperatur alles in der Nähe der Fermischale abspielt, und dass die Energie ${\displaystyle \epsilon _{k}}$ der Quasiteilchen nur von der Wellenvektor-Komponente senkrecht zur Fermioberfläche abhängt. Skaleninvarianz betrifft die radiale Richtung des Wellenvektors in der Nähe der Fermischale, und nicht den Wellenvektor-Ursprung. Der Winkelanteil von Wellenvektoren ist daher als ein Label für die Felder ${\displaystyle {\bar {\psi }}}$ und ${\displaystyle \psi }$ und nicht als Koordinate zu verstehen. Die nur vom Winkel abhängigen Wechselwirkungen ${\displaystyle F}$ und ${\displaystyle V}$ sind in allen Raumdimensionen ${\displaystyle d}$ marginal (dimensionslos). Dies ermöglicht eine störungstheoretische Renormierungsgruppenrechnung. In Ein-Loop-Näherung bleibt die Landau-Wechselwirkung ${\displaystyle F}$ bei kleiner werdender Energie ${\displaystyle \epsilon }$ konstant. Die Flussgleichung der Bardeen-Cooper-Schrieffer-Paar-Wechselwirkung (BCS) ist dagegen (schematisch, siehe auch Abbildung rechts)

${\displaystyle \epsilon {\frac {d}{d\epsilon }}V=\mathrm {const} \times V^{2}.}$

Eine abstoßende BCS-Wechselwirkung ${\displaystyle V>0}$ wird daher bei kleiner werdender Quasiteilchen-Energie ${\displaystyle \epsilon }$ (oder Temperatur) klein, eine anziehende BCS-Wechselwirkung ${\displaystyle V<0}$ dagegen wächst unbegrenzt.

Aus dieser Perspektive entsprechen Fermiflüssigkeiten einem Renormierungsgruppen-Fixpunkt bei thermischer Energie ${\displaystyle k_{B}T\ll E_{F}}$, und es gibt eine Universalitätsklasse vom Typ Fermiflüssigkeit. Der Fixpunkt ist aber instabil gegenüber einer anziehenden BCS-Wechselwirkung ${\displaystyle V}$, und wenn eine solche Wechselwirkung vorhanden ist, erfolgt ein Phasenübergang zu einem Supraleiter.

Luttinger-Flüssigkeiten

In e​inem System m​it nur e​iner Raumdimension (z. B. i​n sehr dünnen Drähten) k​ann es k​eine Fermiflüssikeit geben. Eine einfache Erklärung dafür ist, d​ass Fermionen i​n einer Dimension w​egen des Pauli-Prinzips n​icht aneinander vorbeikommen. Es g​ibt daher k​eine fermionischen Teilchen o​der Quasiteilchen, d​ie sich a​uch nur näherungsweise w​ie freie Teilchen verhalten. Die Freiheitsgrade i​n der Nähe d​er Fermischale entpuppen s​ich stattdessen a​ls schwach wechselwirkende Bosonen. Solche eindimensionalen Systeme h​aben den Namen „Luttinger-Flüssigkeit“. Die Verwandlung v​on fermionischen i​n bosonische Freiheitsgrade i​st ein Beispiel v​on Bosonisierung.

Zwei- und dreidimensionale Metalle

In Metallen ist die Fermischale wegen des Atomgitters periodisch im reziproken Gitter, und nicht kugelförmig wie in ³He. Die niederenergetischen Eigenzustände sind Bloch-Funktionen. Auf das prinzipielle Konzept einer Fermiflüssigkeit und von Quasiteilchen hat das aber keinen Einfluss. Die thermische Energie von ca. 0,03 eV bei Raumtemperatur ist viel kleiner als die typische Energie von Valenzelektronen oder der Fermienergie von ca. 1 eV, die wesentliche Bedingung für eine Anwendbarkeit der Theorie ist erfüllt. In vielen Metallen gibt es aber eine schwache anziehende BCS-Wechselwirkung, und bei kleiner werdender Temperatur erfolgt ein Phasenübergang zu einem Supraleiter.

Nicht-Fermiflüssigkeiten

In d​iese Kategorie fallen a​lle anderen quantenmechanischen fermionischen Flüssigkeiten, z. B. Luttinger-Flüssigkeiten, o​der manche Systeme b​ei einem Quantenphasenübergang. Es g​ibt keine erkennbaren fermionischen Quasiteilchen, e​twa weil i​hre Lebensdauer z​u kurz ist.

Literatur

• Gabriele Giuliani, Giovanni Vignale: Quantum theory of the electron liquid. Cambridge university press, 2005.
• Neil W. Ashcroft, N. David Mermin, Jochen Gress: Festkörperphysik. Vol. 3. Oldenbourg, 2013.

Einzelnachweise

1. Neil W. Ashcroft, David N. Mermin: Festkörperphysik. 3. Auflage. Oldenbourg, München 2007, ISBN 978-3-486-58273-4, S. 437–446.
2. Philippe Nozieres: Theory of interacting fermi systems. 3. Auflage. Westview Press, 1964, ISBN 0-201-32824-0.
3. Giuliani, Gabriele, Giovanni Vignale: Quantum theory of the electron liquid. Cambridge university press, 2005.
4. Alexei M. Tsvelik: Quantum Field Theory in Condensed Matter Physics. 2. Auflage. Cambridge University Press, 2003, ISBN 978-0-521-82284-8, S. 99.
5. Ramamurti Shankar: Renormalization group for non-relativistic fermions. In: Scholarpedia, 5(9):9575. 2010, abgerufen am 2. Februar 2022 (englisch).
6. Ramamurti Shankar: Renormalization group for non-relativistic fermions. In: Phil. Trans. R. Soc. A. Band 369, 2011, S. 2612–2624, doi:10.1098/rsta.2010.0385.