Fahrphysik (Fahrrad)

Das Fahren auf einem Fahrrad ist ein dynamischer Vorgang mit dem Ergebnis, dass ein einspuriges Fahrrad mit seinem auf ihm sitzenden Fahrer nicht umfällt.

Bedingungen dafür sind:[1][2]

eine Mindestgeschwindigkeit
die Balancierfähigkeit des Radfahrers (er lenkt intuitiv zu der Seite, in die das Rad umzufallen droht).

Zusätzlich erleichtert der gyroskopische Effekt durch das automatische Einlenken des Vorderrads beim Kippen des Fahrrads das Fahren, insbesondere das freihändige Fahren.

Das Fahrrad im labilen Gleichgewicht

Ein Fahrrad berührt den Boden an zwei Stellen – den Auflageflächen der Reifen. Eine auch nur geringe Abweichung der Rahmenebene von der Lotrichtung führt beim stehenden Fahrrad zum Umkippen. Sobald der Schwerpunkt nicht mehr über der die Auflageflächen umfassenden und verbindenden Unterstützungsfläche liegt, kippt das Rad um.

Durch abwechselndes starkes Einschlagen des Lenkers kann das Rad etwas um den Radaufstandspunkt des Hinterrads gedreht werden, wodurch sich die Unterstützungsfläche relativ zum Fahrer verschiebt. Dies kommt einer Schwerpunktsverlagerung des Fahrers gleich. Nur geübte Menschen können auf einem stehenden Fahrrad für längere Zeit balancieren ohne abzusteigen. Da diese Probleme beim Geradeausfahren nicht bestehen, muss die Fahrdynamik dafür ausschlaggebend sein.

Das Gleichgewicht während der Fahrt

Einem Umkippen in eine Richtung während der Fahrt wird dadurch entgegengewirkt, dass der Lenker in die gleiche Richtung ausschlägt, eine kurze Kurve einleitet und das Fahrrad nun durch die Fliehkraft zur anderen Seite aufgerichtet wird. Dabei lässt sich ein Überkippen kaum vermeiden, der Lenker muss wiederum in die andere Richtung gelenkt werden und so weiter.

Eine Geradeausfahrt kommt daher einem kaum merkbaren Pendeln um die Gleichgewichtslage zwischen Kippen und Wiederaufrichten gleich. Bei langsamer Fahrt äußert sich das Pendeln durch starke, abwechselnde Lenkausschläge.

Dass die Erzeugung von Fliehkräften zur Kontrolle des Kippwinkels ausreicht, um ein einspuriges Fahrzeug zu steuern, zeigen Versuche mit speziell ausgerüsteten Rädern[3] aber auch die Praxis bei anderen einspurigen Fahrzeugen, bei denen die Kreiselmomente keine oder eine untergeordnete Rolle spielen wie Velogemel, Monoskibob oder Tretroller. Wichtiger werden die Kreiseleffekte beim Freihändig-Fahren, sie tragen aber auch bei normaler Fahrweise zur Stabilisierung des Fahrrads bei.

Kurvenfahrt

Kurveneinfahrt, Kurvenausfahrt

Eine Kurve wird nicht direkt durch ein Drehen des Lenkers in die gewünschte Richtung eingeleitet. Radspuren auf Sand oder Schnee zeigen, dass zunächst eine leichte Lenkbewegung in die entgegengesetzte Richtung erfolgt. Schlüge man für eine Linkskurve einfach nach links ein, dann bewegte sich die Auflagefläche des Reifens nach links unter dem Schwerpunkt weg. Dies bewirkt eine Schräglage nach rechts, die im Folgenden durch die Schwerkraft noch verstärkt wird. Um eine Linkskurve zu fahren, ist aber grundsätzlich eine Neigung nach links notwendig, damit das Rad nicht nach außen kippt.

Eine andere Möglichkeit zur Einleitung einer Kurvenfahrt besteht in einer leichten Gewichtsverlagerung zur Kurveninnenseite. Anschließend wird die Schräglage durch Lenken stabilisiert. Damit wird ein neues Gleichgewicht erreicht, in dem das Kippmoment durch die Fliehkraft ausgeglichen wird.

Um die Kurvenfahrt zu beenden muss zunächst etwas mehr eingelenkt werden als es der Querneigung entspricht. Das Moment aus der Fliehkraft wird größer als das Moment der Gewichtskraft, wodurch sich das Rad aufrichtet.

Bestimmung des Neigungswinkels

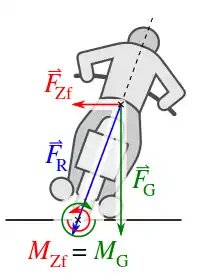
Zweirad bei stationärer Kurvenfahrt

Eine Kurve kann als Teil einer Kreisbahn betrachtet werden. Legt sich der Fahrer in die Kurve, ist der Neigungswinkel abhängig von Fahrgeschwindigkeit und Kurvenradius. Je schneller die Fahrt und je enger die Kurve, desto größer muss der einzunehmende Neigungswinkel sein. Dieser ist eindeutig bestimmbar: Die Verbindungslinie zwischen Schwerpunkt und Unterstützungsfläche muss nämlich in Richtung der Resultierenden $F_{\text{R}}$ von Fliehkraft $F_{\text{Zf}}$ und Gewichtskraft $F_{\text{G}}$ verlaufen. Für den Neigungswinkel $\alpha$ zwischen der Resultierenden und der Senkrechten gilt daher:

\tan {\alpha }={\frac {F_{\text{Zf}}}{F_{G}}}={\frac {v^{2}}{r\;g}}

Dabei ist $v$ die Geschwindigkeit, $r$ der Kurvenradius, und $g$ die Schwerebeschleunigung.

Da $\tan {\alpha }$ zugleich das Verhältnis von Zentripetalkraft und Normalkraft ist, ergibt sich somit für den erforderlichen Kraftschlussbeiwert auf ebener Fahrbahn:

\mu =\tan {\alpha }

Die Haftreibung der Laufräder bestimmt nun den maximalen Neigungswinkel, dessen Überschreitung zum Wegrutschen eines Rades und zum Sturz führt. Vor engen Kurven und auf schmierigen, schotterigen oder glattem Untergrund ist also ein Abbremsen notwendig, weil die Reibung sonst nicht ausreicht, die erforderliche Zentripetalkraft aufzubringen. Der maximale Neigungswinkel wird durch den Haftreibungskoeffizienten $\mu _{H}$ begrenzt:

\tan \alpha \leq \mu _{H}

Mit dem linearen Einspurmodell lässt sich eine Gleichung für den Zusammenhang zwischen Lenkeinschlag und Bahnkrümmung ableiten:

{\frac {1}{r}}\approx {\frac {\delta }{L}}

Dabei ist $L$ der Radstand und $\delta$ der Lenkeinschlag. Für den Neigungswinkel ergibt sich somit:

\tan \alpha \approx {\frac {v^{2}}{L\,g}}\cdot \delta

Die Gleichung verdeutlicht auch, warum eine Mindestgeschwindigkeit beim Fahrradfahren erforderlich ist. Bei sehr geringen Geschwindigkeiten müssen bereits kleine Neigungswinkel durch große Lenkeinschläge ausgeglichen, bzw. bei Geradeausfahrt überkompensiert werden. Oberhalb der Mindestgeschwindigkeit kann die zum Kreismittelpunkt gerichtete Zentripetalkraft, durch kleinere dosierte Lenkeinschläge aufgebracht werden.

Überhöhung

Der Kurvenradius kann erheblich verkleinert werden, wenn die Fahrbahn nicht eben, sondern in Richtung Kurvenmittelpunkt nach unten geneigt ist (Überhöhung). Ist der erforderliche Neigungswinkel gleich groß wie der Überhöhungswinkel, kann die Bahn seitenkraftfrei befahren werden. Diese Hilfe machen sich sowohl Cyclo-Cross-Fahrer und Mountainbiker als auch Bahnradfahrer zunutze:

Im Cyclocross- und Mountainbike-Sport nutzt man z. B. ausgefurchte Kurven, die hierdurch eine Überhöhung aufweisen, um Kurven schneller zu durchfahren.
Im Bahnradsport weisen die Radrennbahnen grundsätzlich in den Kurven Überhöhungen zwischen 30 Grad (lange Freiluft-Zementbahnen mit größerer Haftreibung) und gewöhnlich 45 Grad Überhöhungswinkel auf (in Ausnahmefällen sogar darüber: die nicht mehr existierenden Bahnen in Münster und Frankfurt am Main hatten Überhöhungen von über 55 Grad).

Fahrereinfluss bei Kurvenfahrten

Dem Fahrer ist beim Kurvenfahren die Feinabstimmung überlassen, ohne die eine kontrollierte Fahrt nicht möglich wäre. Beim sportlichen Radfahren (Radrennsport) sind zum erfolgreichen Durchfahren von Kurven weitere Techniken unerlässlich. Beispielsweise muss der Fahrer eine Körperspannung aufbauen, was durch Durchdrücken des fast gestreckten kurvenäußeren Beines (Pedale im tiefsten Punkt) bewirkt wird. Im Mountainbikesport hingegen, wo es eher um schnelle Verlagerung des Körperschwerpunktes aufgrund der Bodenbeschaffenheiten geht, hat sich eine Waagrechtstellung der Pedale als eher zweckmäßig erwiesen.

Ausweichmanöver

Bei Kurven, die im Zuge von kurzen Ausweichmanövern gefahren werden, ist die Technik des Gegenlenkens, um das Kippen einzuleiten, nicht notwendig, wenn der Fahrer anschließend die Fahrt auf der ursprünglichen Fahrlinie fortsetzen möchte. Statt der beschriebenen Technik lenkt der Fahrer das Fahrrad an dem Hindernis vorbei, während sein Körperschwerpunkt sich fast geradeaus weiterbewegt. Demzufolge ist diese Technik auch nur zum Ausweichen vor bodennahen Hindernissen, Schlaglöchern usw. geeignet. Wird sie in der falschen Situation angewandt, führt sie zu schweren Stürzen. Die Entscheidung über die Technik trifft der Fahrer nicht bewusst, sondern in Zehntelsekundenschnelle intuitiv.

Freihändig Fahren

Fahrrad mit Koordinatenachsen

Bei freihändigem Fahren bewirkt man durch das seitliche Neigen des Körpers eine Lenkbewegung. Je mehr man das Fahrrad neigt, desto mehr Lenkeinschlag wird entstehen, in einem gewissen Rahmen. Freihändiges Fahren ist bei langsamer Fahrt nahezu unmöglich. Erst der weiter unten beschriebene Nachlauf und die Kreiselkräfte ermöglichen dies, indem sie bei einer Radneigung einen kontrollierbaren Lenkeinschlag auslösen und so das Rad wieder in die gerade Fahrlinie zurückbringen, beziehungsweise eine stabile Kurvenfahrt ermöglichen. Der sich selbst einstellende Lenkeinschlag unterstützt auch das nicht-freihändige Fahren.

Kreiseleffekte – Stabilisation durch Präzession

Das Vorderrad stellt einen symmetrischen, nutationsfreien Kreisel dar; die Drehimpuls-, Rotations- und Figurenachsen sind identisch. Beim Versuch, auf einem Drehsessel ein solches sich drehendes Vorderrad um die Horizontale zu kippen, stellt man fest, dass sich der Sessel zu drehen anfängt. Um den Effekt allgemein zu formulieren, wird zuerst angenommen, ein solcher Kreisel dreht sich um die Rotationsachse. Er bleibt fortan in Bewegung. Wird er dann im weiteren um eine Senkrechte etwas gedreht, ohne sonstige Beeinflussung, dreht er sich auch etwas um die Längsachse. Der Effekt heißt Präzession.

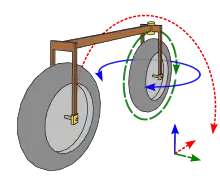
Das Modell kann auf 2 Arten auf das Vorderrad angewendet werden.

Kippt das Rad etwas um die rote Längsachse, dreht sich das Rad etwas um die blaue vertikale Achse. Ein Kippen des Vorderrads und damit des ganzen Fahrrads verursache eine Lenkung, der Lenker dreht sich in die Richtung der Neigung.[4]

Dreht man andererseits mit dem Lenker das rotierende Vorderrad um die blaue Vertikalachse nach links, kippt es um die rote Längsachse nach rechts. Lenken verursacht das Kippen des Fahrrads in die entgegengesetzte Richtung.

Konstruktionsmerkmale eines Fahrrads, die das Fahren beeinflussen

Fahrrad: Positiver Nachlauf, Radstand

Nachlauf

Als Nachlauf wird der Abstand zwischen dem Vorderradaufstandspunkt und dem Punkt, in dem die gedachte Verlängerung der Lenkachse den Boden trifft, dem so genannten Spurpunkt, bezeichnet. Geometrisch festgelegt wird der Nachlauf durch Laufradradius, Steuerkopfwinkel (zwischen Lenkachse und Boden) und der Gabelbiegung (senkrechter Abstand von Nabe zur Lenkachse). Der Name rührt daher, dass das Rad bei Lenkbewegungen dem Spurpunkt „hinterherläuft“. Ist der Nachlauf positiv, so befindet sich der Spurpunkt wie in der Abbildung dargestellt in Fahrtrichtung vor dem Aufsetzpunkt. Die Größe des Nachlaufs liegt meist zwischen fünf und siebeneinhalb Zentimeter.

Der Nachlauf ist wohl die wichtigste bauliche Unterstützung im Bemühen gegen das Umfallen während des Geradeausfahrens. Er wirkt auf folgende Arten:

Die bei Radneigung an der Vorderachse angreifende Schwerkraft des Vorderrades und des Lenkers bewirkt einen Lenkereinschlag in Richtung der Neigung. Dieser Effekt ist gut sichtbar, hält man den Sattel fest und neigt das Rad dreht sich das Vorderrad. Ebenso eindrehend ist das Moment der Radaufstandskraft um die Lenkachse. Beide Effekte nehmen mit dem Kippwinkel zu und unterstützen den Fahrer. Durch den Lenkereinschlag wird eine Kurvenfahrt eingeleitet, bei der die Fliehkraft das Rad aufrichtet.[5]
Die Seitenführungskraft erzeugt ein rückstellendes Moment. Bei stationärer Kurvenfahrt liegt die Resultierende aus Seitenkraft und Radlast etwa in der Ebene des Vorderrads. Die Momente der beiden Kräfte um die Lenkachse heben sich somit auf. Insgesamt ist der Lenker damit fast momentenfrei.

Dass ein Fahren mit einem negativen Nachlauf nur schwer möglich ist, zeigt das Experiment des Chemikers David E. H. Jones. Er versuchte im Jahr 1970 ein Fahrrad zu konstruieren, das unfahrbar ist. Die meisten entwickelten Radtypen waren jedoch mehr oder weniger trotzdem nutzbar. Erst ein Rad mit negativem Nachlauf war „sehr knifflig“ zu steuern und besaß vernachlässigbare Selbststabilisierung.[6]

Radstand

Ein Fahrrad mit zwei Laufrädern berührt den Boden in zwei Punkten. Der Abstand dieser Punkte heißt Radstand. Die Reaktion des Fahrrads auf einen Lenkeinschlag ist näherungsweise umgekehrt proportional zum Radstand. Das etwas träge Verhalten von Rädern mit langem Radstand, etwa Tandems, lässt sich hierdurch erklären.

Ein Fahrrad mit weit auseinanderstehenden Laufrädern ist weniger wendig, bleibt aber der Richtung treu. Mit nahe beieinanderstehenden Laufrädern reagiert es stärker auf Lenkbewegungen, dabei stellt sich aber ein eher nervöser Geradeauslauf ein. Seine Wendigkeit wird beim Rennrad genutzt.

Vor allem nicht betont sportlich konstruierte Fahrräder haben einen Radstand von deutlich über einen Meter, ein Tandem gar zwei. In Wettbewerben verwendete Rennräder weisen i. d. R. einen Radstand von 97 bis 100 Zentimeter auf.

Um den Radstand zu messen, misst man den Abstand der Radmittelpunkte (Nabenachsenmittelpunkt) bei geradeaus ausgerichtetem Lenker, die den gleichen Abstandhaben wie die Kontaktpunkte am Boden, sofern Vorder- und Hinterrad den gleichen Radius besitzen.

Laufradgröße und -gewicht

Je größer im Durchmesser und schwerer die Räder sind, desto größer sind die Kreiselmomente. Bei einem normalen Gebrauchsrad (Laufraddurchmesser 60 cm, Masse 1 kg) sind die Kreiselwirkungen etwa fünfmal so groß wie bei einem Kinderrad (30 cm; 0,4 kg). Korrekterweise hängt das Kreiselmoment natürlich nicht von der Masse des Laufrades, sondern von der Verteilung der Masse im Laufrad (Trägheitsmoment bzgl. der Achse) ab; beispielsweise hat ein Laufrad mit einer „schweren“ Felge ein größeres Kreiselmoment als ein gleich schweres Laufrad mit einer „leichten“ Felge mit einer „schweren“ Nabenschaltung. Konstruiert werden Fahrräder aber eher unter dem Gesichtspunkt des Energiesparens und daher so leicht wie möglich.

Sitzposition

Verlagert der Fahrer sein Gewicht auf das Hinterrad, sind geringere Lenkkräfte nötig. Dies führt allerdings zu Übersteuern und flatterigem Fahrverhalten aufgrund zu weiter oder zu schneller Richtungskorrekturen. Beugt man sich vor und belastet das Vorderrad, sind größere Lenkkräfte nötig. Man untersteuert und erreicht ein schwankendes Fahrverhalten wegen zu später und geringer Korrekturen.

Als Erfahrungswert gilt, dass ein ausgewogenes Fahrverhalten gewährleistet ist, wenn 55 bis 60 % des Gesamtgewichts von Fahrrad und Fahrer auf dem Hinterrad lasten.

Rahmengröße

Abgesehen vom Radstand hat die Rahmengröße keinen direkten Einfluss auf das Fahrverhalten. Dennoch erleichtert die optimale Anpassung an die Körpermaße die Kontrolle über das Fahrrad. Für jeden Fahrradtyp gibt es hierzu eigene Richtlinien, für die die eigene Schrittlänge zu beachten ist. Zu empfehlen ist bei sportlicher Fahrweise die Wahl eines kleineren, bei tourenorientierter Fahrweise die Wahl eines größeren Rahmens.

Literatur

Michael Gressmann: Fahrradphysik und Biomechanik. Moby Dick Verlag, Kiel 2002, ISBN 3-89595-023-8.
Frank Bollerey: Das Problem des Gleichgewichts beim Fahrradfahren aus physikalischer Sicht. Diplomarbeit. Universität Kassel, 1999.
Hans-Joachim Schlichting: Zur Gleichgewichtsproblematik beim Fahrradfahren. In: technic-didact. 9/4, 1984, S. 257. (Download 57 kB pdf)
H. Joachim Schlichting, Wilfried Suhr: Physik des Fahrradfahrens: Moderne Zentauren, Physik in unserer Zeit, Band 38, 2007, Nr. 4, S. 184–188
H. Joachim Schlichting, Wilfried Suhr: Physik des Fahrradfahrens: Gleichgewicht auf zwei Rädern, Physik in unserer Zeit, Band 38, 2007, Nr. 5, S. 238–241
H. Joachim Schlichting, Wilfried Suhr: Physik des Fahrradfahrens: Mit Pedalkraft gegen Berg und Wind, Physik in unserer Zeit, Band 38, 2007, Nr. 6, S. 294–298
H. Joachim Schlichting, Wilfried Suhr: Das Fahrrad als alltägliches Verkehrsmittel: Zweirädrige Energiesparbüchse, Physik in unserer Zeit, Band 39, 2008, Nr. 2, S. 86–89
Gert Franke, Wilfried Suhr, Falk Rieß: Physikalische Modelle der Fahrraddynamik. Warum ist Fahrradfahren so einfach ?, Pro Velo, Band 21, 1990, Heft 5
David E. H. Jones: The Stability of the Bicycle, Physics Today, Band 23, April 1970 S. 34–40
Roger Erb: Zum Problem der Stabilität beim Fahrradfahren. In: MNU. 5/54, 2001, S. 279–284. (online)
Felix Klein, Arnold Sommerfeld: Über die Theorie des Kreisels. Nachdruck der Erstauflage von 1897, 1898, 1903, 1910. Johnson Repr. u. a., New York u. a. 1965, ISBN 0-384-29720-X.
F. J. W. Whipple: The stability of motion of a bicycle, Quarterly Journal of Pure and Applied Math., Band 30, 1899, S. 312
Archibald Sharp: Bicycles & tricycles; an elementary treatise on their design and construction (1896), (archive.org)

Weblinks

Wiktionary: Rad fahren – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Fahrradfahren – Sammlung von Bildern

Wikibooks: Fahrrad fahren lernen – Lern- und Lehrmaterialien

Einzelnachweise

Für die Balancesteuerung reichte eine einzige Zeile Code. auf: heise.de, 2. November 2012.
Neues Freihand-Fahrrad: Die Masse macht's. In: Spiegel online. 15. April 2011.
J. D. G. Kooijman, A. L. Schwab, J. P. Meijaard, J. M. Papadopoulos, A. Ruina: A Bicycle Can Be Self-Stable Without Gyroscopic or Caster Effects. In: Science. Band 332, Nr. 6027, 2011, S. 339–342, doi:10.1126/science.1201959.,
Die Federung, Fahrwerk und Federung („Warum kippen wir mit einem einspurigen Fahrzeug eigentlich nicht einfach um?“), oelsumpfonline.de, 2004.
Roger Erb: Zum Problem der Stabilität beim Fahrradfahren. In: MNU – Verband zur Förderung des Mint-Unterrichts. Nr. 5/54, 2001, S. 279–284. (online) (PDF 489 KB S. 6–9)
David E. H. Jones: The Stability of the Bicycle. In: Physics Today. 23 (April 1970) S. 34–40. ( PDF (Memento vom 30. Oktober 2008 im Internet Archive), 9 MB, englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Für die Balancesteuerung reichte eine einzige Zeile Code. auf: heise.de, 2. November 2012.

[2] Neues Freihand-Fahrrad: Die Masse macht's. In: Spiegel online. 15. April 2011.

[3] J. D. G. Kooijman, A. L. Schwab, J. P. Meijaard, J. M. Papadopoulos, A. Ruina: A Bicycle Can Be Self-Stable Without Gyroscopic or Caster Effects. In: Science. Band 332, Nr. 6027, 2011, S. 339–342, doi:10.1126/science.1201959.,

[4] Die Federung, Fahrwerk und Federung („Warum kippen wir mit einem einspurigen Fahrzeug eigentlich nicht einfach um?“), oelsumpfonline.de, 2004.

[5] Roger Erb: Zum Problem der Stabilität beim Fahrradfahren. In: MNU – Verband zur Förderung des Mint-Unterrichts. Nr. 5/54, 2001, S. 279–284. (online) (PDF 489 KB S. 6–9)

[Jones1970-6] David E. H. Jones: The Stability of the Bicycle. In: Physics Today. 23 (April 1970) S. 34–40. ( PDF (Memento vom 30. Oktober 2008 im Internet Archive), 9 MB, englisch).