Dilogarithmus

In der Mathematik werden verschiedene spezielle Funktionen als Dilogarithmus bezeichnet. Der klassische Dilogarithmus ist ein Spezialfall des Polylogarithmus.

Klassischer Dilogarithmus

Werte des klassischen Dilogarithmus auf der reellen Achse. (Der Imaginärteil ist dort identisch Null.)

→ Hauptartikel: Polylogarithmus

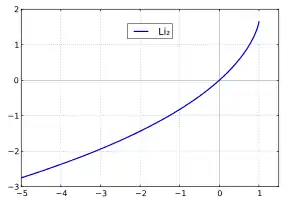
Der klassische Dilogarithmus ist für komplexe Zahlen ${\displaystyle z}$ mit ${\displaystyle |z|<1}$ definiert durch die Potenzreihe

${\displaystyle \operatorname {Li} _{2}(z)=\sum _{k=1}^{\infty }{\frac {z^{k}}{k^{2}}}}$.

Er lässt sich durch analytische Fortsetzung auf ${\displaystyle \mathbb {C} \setminus \left[1,\infty \right]}$ fortsetzen:

${\displaystyle \operatorname {Li} _{2}(z)=-\int _{0}^{z}{\frac {\ln(1-t)}{t}}\,\mathrm {d} t}$.

(Hierbei muss entlang eines Weges in ${\displaystyle \mathbb {C} \setminus \left[1,\infty \right]}$ integriert werden.)

Bloch-Wigner-Dilogarithmus

Der Bloch-Wigner-Dilogarithmus ist für ${\displaystyle z\in \mathbb {C} }$ definiert durch

${\displaystyle \operatorname {D} _{2}(z)=\operatorname {Im} (\operatorname {Li} _{2}(z))+\arg(1-z)\ln(|z|)}$.

Er ist wohl-definiert und stetig, auch in ${\displaystyle \left[1,\infty \right]}$.

Er ist analytisch in ${\displaystyle \mathbb {C} \setminus \left\{0,1\right\}}$, in 0 und 1 hat er Singularitäten vom Typ ${\displaystyle r\ln(r)}$.

Rogers-Dilogarithmus

Der Rogers-Dilogarithmus ist definiert durch

${\displaystyle L(x)={\frac {6}{\pi ^{2}}}\left(\operatorname {Li} _{2}(x)+{\frac {1}{2}}\ln(x)\ln(1-x)\right)}$

für ${\displaystyle 0<x<1}$.

Eine andere gebräuchliche Definition ist

${\displaystyle R(x)=\operatorname {Li} _{2}(x)+{\frac {1}{2}}\ln(x)\ln(1-x)-{\frac {\pi ^{2}}{6}}}$.

Diese hängt mit der erstgenannten via

${\displaystyle R(x)={\frac {\pi ^{2}}{6}}(L(x)-1)}$

zusammen.

Man kann ${\displaystyle R}$ (unstetig) auf ganz ${\displaystyle \mathbb {R} }$ fortsetzen durch ${\displaystyle R(1)=0,R(0)=-{\frac {\pi ^{2}}{6}}}$ und

${\displaystyle R(x)=\left\{{\begin{array}{ll}-R(1/x)\ &{\mbox{für}}\ x>1\\-R(x/(x-1))\ &{\mbox{für}}\ x<0\end{array}}\right\}}$.

Elliptischer Dilogarithmus

Sei ${\displaystyle E}$ eine über ${\displaystyle \mathbb {Q} }$ definierte elliptische Kurve. Mittels der Weierstraßschen ℘-Funktion lässt sie sich mittels eines Gitters ${\displaystyle \Lambda =\left\{1,\tau \right\}}$ parametrisieren durch

${\displaystyle \mathbb {C} /\Lambda \rightarrow E(\mathbb {C} )}$

${\displaystyle u}$ mod ${\displaystyle \Lambda \mapsto (p(u),p^{\prime }(u))}$.

Der elliptische Dilogarithmus ${\displaystyle D^{E}\colon E(\mathbb {C} )\rightarrow \mathbb {C} }$ ist dann definiert durch

${\displaystyle D^{E}(p(u),p^{\prime }(u))=\sum _{n=-\infty }^{\infty }D_{2}(e^{2\pi i(n\tau +u)})}$,

wobei ${\displaystyle D_{2}}$ den Bloch-Wigner-Dilogarithmus bezeichnet.

Der elliptische Dilogarithmus stimmt bis auf rationale Vielfache von ${\displaystyle \pi }$ mit dem Wert ${\displaystyle L(E,2)}$ der L-Funktion überein.[1]

Spezielle Werte

Klassischer Dilogarithmus

Für die folgenden Zahlen lassen sich ${\displaystyle z}$ und ${\displaystyle \operatorname {Li} _{2}(z)}$ in geschlossener Form darstellen:

${\displaystyle \operatorname {Li} _{2}(-1)=-{\frac {{\pi }^{2}}{12}},\qquad \operatorname {Li} _{2}(0)=0,}$

${\displaystyle \operatorname {Li} _{2}\left({\frac {1}{2}}\right)={\frac {{\pi }^{2}}{12}}-{\frac {\ln ^{2}(2)}{2}},\qquad \operatorname {Li} _{2}(1)={\frac {{\pi }^{2}}{6}}}$,

${\displaystyle \operatorname {Li} _{2}\left(-{\frac {{\sqrt {5}}-1}{2}}\right)=-{\frac {{\pi }^{2}}{15}}+{\frac {1}{2}}\ln ^{2}\left({\frac {{\sqrt {5}}+1}{2}}\right),\qquad \operatorname {Li} _{2}\left(-{\frac {{\sqrt {5}}+1}{2}}\right)=-{\frac {{\pi }^{2}}{10}}-\ln ^{2}\left({\frac {{\sqrt {5}}+1}{2}}\right),}$

${\displaystyle \operatorname {Li} _{2}\left({\frac {3-{\sqrt {5}}}{2}}\right)={\frac {{\pi }^{2}}{15}}-\ln ^{2}\left({\frac {{\sqrt {5}}+1}{2}}\right),\qquad \operatorname {Li} _{2}\left({\frac {{\sqrt {5}}-1}{2}}\right)={\frac {{\pi }^{2}}{10}}-\ln ^{2}\left({\frac {{\sqrt {5}}+1}{2}}\right)}$.

Mit der sechsten Einheitswurzel ${\displaystyle \omega ={\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i}$ und der Gieseking-Konstante ${\displaystyle V_{0}=1{,}0149\ldots }$ hat man außerdem

${\displaystyle \operatorname {Li} _{2}(\omega )={\frac {\pi ^{2}}{36}}+V_{0}i,\qquad \operatorname {Li} _{2}(\omega ^{2})=-{\frac {\pi ^{2}}{18}}+{\frac {2}{3}}V_{0}i,}$

${\displaystyle \operatorname {Li} _{2}(1+\omega )={\frac {\pi ^{2}}{9}}+\left({\frac {2}{3}}V_{0}+{\frac {1}{3}}\ln(3)\pi \right)i,\qquad \operatorname {Li} _{2}\left({\frac {1}{1+\omega }}\right)={\frac {5\pi ^{2}}{72}}-{\frac {1}{8}}\ln(3)+\left(-{\frac {2}{3}}V_{0}+{\frac {1}{12}}\ln(3)\pi \right)i}$.

Bloch-Wigner-Dilogarithmus

Werte des Bloch-Wigner-Dilogarithmus können bisher nur numerisch berechnet werden und man kennt nur wenige algebraische Relationen zwischen Werten des Bloch-Wigner-Dilogarithmus. Eine Vermutung von John Milnor besagt für ${\displaystyle N\geq 3}$:

die Zahlen ${\displaystyle D_{2}(e^{2\pi i{\frac {j}{N}}})}$ für ${\displaystyle 0<j<{\frac {N}{2}}}$ und ${\displaystyle \operatorname {ggT} (j,N)=1}$ sind linear unabhängig über ${\displaystyle \mathbb {Q} }$.

Rogers-Dilogarithmus

Es gibt zahlreiche algebraische Identitäten zwischen Werten von ${\displaystyle L}$ in rationalen oder algebraischen Argumenten. Beispiele spezieller Werte sind

${\displaystyle L(0)=0,\quad L\left({\frac {1}{2}}\right)={\frac {1}{2}},\quad L(1)=1,\quad L\left({\frac {3-{\sqrt {5}}}{2}}\right)={\frac {2}{5}},\quad L\left({\frac {{\sqrt {5}}-1}{2}}\right)={\frac {3}{5}}}$.

Mit der sechsten Einheitswurzel ${\displaystyle \omega ={\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i}$ und der Gieseking-Konstante ${\displaystyle V_{0}=1,0149...}$ hat man

${\displaystyle R(\omega )=-{\frac {\pi ^{2}}{12}}+V_{0}i,\qquad R(\omega ^{2})=-{\frac {\pi ^{2}}{6}}+\left({\frac {2}{3}}V_{0}+{\frac {1}{6}}\ln(3)\pi \right)i,}$

${\displaystyle R(1+\omega )=\left({\frac {2}{3}}V_{0}+{\frac {1}{6}}\ln(3)\pi \right)i,\qquad R\left({\frac {1}{1+\omega }}\right)=-{\frac {\pi ^{2}}{12}}-{\frac {1}{8}}\ln(3)+{\frac {1}{8}}\ln ^{2}(3)+\left(-{\frac {2}{3}}V_{0}+{\frac {1}{12}}\ln(3)\pi \right)i}$.

Funktionalgleichungen

Klassischer Dilogarithmus

Der klassische Dilogarithmus genügt zahlreichen Funktionalgleichungen, zum Beispiel

${\displaystyle \operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(-z)={\frac {1}{2}}\operatorname {Li} _{2}(z^{2}),}$

${\displaystyle \operatorname {Li} _{2}(1-z)+\operatorname {Li} _{2}\left(1-{\frac {1}{z}}\right)=-{\frac {\ln ^{2}(z)}{2}},}$

${\displaystyle \operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1-z)={\frac {{\pi }^{2}}{6}}-\ln(z)\cdot \ln(1-z),}$

${\displaystyle \operatorname {Li} _{2}(-z)-\operatorname {Li} _{2}(1-z)+{\frac {1}{2}}\operatorname {Li} _{2}(1-z^{2})=-{\frac {{\pi }^{2}}{12}}-\ln(z)\cdot \ln(z+1),}$

${\displaystyle \operatorname {Li} _{2}(z)+\operatorname {Li} _{2}\left({\frac {1}{z}}\right)=-{\frac {\pi ^{2}}{6}}-{\frac {1}{2}}\ln ^{2}(-z),}$

${\displaystyle \operatorname {Li} _{2}(z)-{\frac {1}{4}}\operatorname {Li} _{2}(z^{2})=\int _{0}^{1}{\frac {\operatorname {arcsin} (xz)}{\sqrt {1-x^{2}}}}\,\mathrm {d} x}$. Daraus folgt: ${\displaystyle \operatorname {Li} _{2}(1)={\frac {{\pi }^{2}}{6}}}$.

Bloch-Wigner-Dilogarithmus

Der Bloch-Wigner-Dilogarithmus genügt den Identitäten

${\displaystyle \operatorname {D} _{2}(z)=\operatorname {D} _{2}\left(1-{\frac {1}{z}}\right)=\operatorname {D} _{2}\left({\frac {1}{1-z}}\right)=-\operatorname {D} _{2}\left({\frac {1}{z}}\right)=-\operatorname {D} _{2}(1-z)=-\operatorname {D} _{2}\left({\frac {-z}{1-z}}\right)}$

und der 5-Term-Relation

${\displaystyle \operatorname {D} _{2}(x)+\operatorname {D} _{2}(y)+\operatorname {D} _{2}\left({\frac {1-x}{1-xy}}\right)+\operatorname {D} _{2}(1-xy)+\operatorname {D} _{2}\left({\frac {1-y}{1-xy}}\right)=0}$.

Rogers-Dilogarithmus

Der Rogers-Dilogarithmus erfüllt die Beziehung

${\displaystyle L(x)+L(1-x)=1}$

und Abels Funktionalgleichung

${\displaystyle L(x)+L(y)=L(xy)+L\left({\frac {x(1-y)}{1-xy}}\right)+L\left({\frac {y(1-x)}{1-xy}}\right)}$.

Für ${\displaystyle R}$ hat man

${\displaystyle R(x)+R(1-x)=-{\frac {\pi ^{2}}{6}}}$

und die 5-Term-Relation

${\displaystyle R(x)-R(y)+R\left({\frac {y}{x}}\right)-R\left({\frac {1-x^{-1}}{1-y^{-1}}}\right)+R\left({\frac {1-x}{1-y}}\right)=0}$,

insbesondere ist ${\displaystyle R}$ eine wohldefinierte Funktion auf der Bloch-Gruppe.

Integration von Funktionen

Folgende Gleichung gilt für ${\displaystyle v\not =0}$ und ${\displaystyle {\frac {uv-tw}{v}}>0}$:

${\displaystyle {\frac {\ln(tx+u)}{vx+w}}={\frac {\mathrm {d} }{\mathrm {d} x}}\left[{\frac {1}{v}}\ln \left({\frac {uv-tw}{v}}\right)\ln(vx+w)-{\frac {1}{v}}\operatorname {Li} _{2}\left(-t{\frac {vx+w}{uv-tw}}\right)\right]}$

Beispiel:

${\displaystyle {\begin{aligned}\int _{0}^{5}{\frac {\ln(x+2)}{3x+4}}\mathrm {d} x&=\left[{\frac {1}{3}}\ln \left({\frac {2}{3}}\right)\ln(3x+4)-{\frac {1}{3}}\operatorname {Li} _{2}\left(-{\frac {3}{2}}x-2\right)\right]_{(x=5)}-\left[{\frac {1}{3}}\ln \left({\frac {2}{3}}\right)\ln(3x+4)-{\frac {1}{3}}\operatorname {Li} _{2}\left(-{\frac {3}{2}}x-2\right)\right]_{(x=0)}\\&=-{\frac {1}{3}}\ln \left({\frac {3}{2}}\right)\ln \left({\frac {19}{4}}\right)-{\frac {1}{3}}\operatorname {Li} _{2}\left(-{\frac {19}{2}}\right)+{\frac {1}{3}}\operatorname {Li} _{2}(-2)\\\end{aligned}}}$

Weitere Funktionen lassen sich mit dem Dilogarithmus integrieren:

${\displaystyle {\frac {\operatorname {artanh} (x)}{x}}={\frac {\mathrm {d} }{\mathrm {d} x}}\left[\operatorname {Li} _{2}(x)-{\frac {1}{4}}\operatorname {Li} _{2}(x^{2})\right]}$

${\displaystyle {\frac {\operatorname {artanh} (x)}{x{\sqrt {1-x^{2}}}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\left[2\operatorname {Li} _{2}\left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)-{\frac {1}{2}}\operatorname {Li} _{2}\left({\frac {x^{2}}{(1+{\sqrt {1-x^{2}}})^{2}}}\right)\right]}$

${\displaystyle {\frac {\operatorname {artanh} (x)}{x(1-x^{2})}}={\frac {\mathrm {d} }{\mathrm {d} x}}\left[{\frac {1}{2}}\operatorname {Li} _{2}\left({\frac {2x}{x+1}}\right)+{\frac {1}{2}}\operatorname {artanh} (x)^{2}\right]}$

${\displaystyle {\frac {\operatorname {arsinh} (x)}{x}}={\frac {\mathrm {d} }{\mathrm {d} x}}\left[{\frac {1}{2}}\operatorname {Li} _{2}\left(2x({\sqrt {x^{2}+1}}-x)\right)+{\frac {1}{2}}\operatorname {arsinh} (x)^{2}\right]}$

Deswegen gilt: ${\displaystyle \int _{0}^{1/2}{\frac {\operatorname {arsinh} (x)}{x}}\mathrm {d} x={\frac {1}{2}}\operatorname {Li} _{2}\left({\frac {1}{2}}{\sqrt {5}}-{\frac {1}{2}}\right)+{\frac {1}{2}}\operatorname {arsinh} \left({\frac {1}{2}}\right)^{2}={\frac {\pi ^{2}}{20}}}$

Daraus folgt: ${\displaystyle \sum _{k=0}^{\infty }{\frac {(-1)^{k}(2k)!}{16^{k}(2k+1)^{2}(k!)^{2}}}={\frac {\pi ^{2}}{10}}}$

${\displaystyle {\frac {\operatorname {arsinh} (x)}{x{\sqrt {x^{2}+1}}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\left[2\operatorname {Li} _{2}\left({\frac {x}{{\sqrt {x^{2}+1}}+1}}\right)-{\frac {1}{2}}\operatorname {Li} _{2}\left({\frac {x^{2}}{({\sqrt {x^{2}+1}}+1)^{2}}}\right)\right]}$

${\displaystyle {\frac {\operatorname {arsinh} (x)}{x(x^{2}+1)}}={\frac {\mathrm {d} }{\mathrm {d} x}}\left[\operatorname {Li} _{2}\left({\frac {x}{\sqrt {x^{2}+1}}}\right)-{\frac {1}{4}}\operatorname {Li} _{2}\left({\frac {x^{2}}{x^{2}+1}}\right)\right]={\frac {\mathrm {d} }{\mathrm {d} x}}\left[\operatorname {Li} _{2}\left(2x({\sqrt {x^{2}+1}}-x)\right)-{\frac {1}{4}}\operatorname {Li} _{2}\left(4x({\sqrt {x^{2}+1}}-x)^{2}{\sqrt {x^{2}+1}}\right)\right]}$

Siehe auch

• Quantendilogarithmus
• Trilogarithmus

Weblinks

• Eric W. Weisstein: Dilogarithm. In: MathWorld (englisch).
• Don Zagier: The dilogarithm function (PDF; 1,5 MB)
• Matilde Lalin: The dilogarithm
• Dupont, Zickert: A dilogarithmic formula for the Cheeger-Chern-Simons class

Einzelnachweise

1. K₂ and L-functions of elliptic curves