Copula (Mathematik)

Eine Copula (Pl. Copulas o​der Copulae) i​st eine Funktion, d​ie einen funktionalen Zusammenhang zwischen d​en Randverteilungsfunktionen verschiedener Zufallsvariablen u​nd ihrer gemeinsamen Wahrscheinlichkeitsverteilung angeben kann.

Mit i​hrer Hilfe k​ann man stochastische Abhängigkeit deutlich flexibler modellieren a​ls beispielsweise m​it Korrelationskoeffizienten.

Definition

Eine Copula ist eine multivariate Verteilungsfunktion ${\displaystyle C\colon [0,1]^{n}\rightarrow [0,1]}$, deren eindimensionale Randverteilungen gleichverteilt über dem Intervall ${\displaystyle [0,1]}$ sind. Formal ausgedrückt bedeutet dies folgendes:

• ${\displaystyle C}$ ist multivariate Verteilungsfunktion, das heißt
  • ${\displaystyle \forall u\in [0,1]^{n}\colon \min\{u_{1},\dotsc ,u_{n}\}=0\implies C(u)=0}$,
  • ${\displaystyle C}$ ist ${\displaystyle n}$-steigend, das heißt für jedes Hyperrechteck ${\displaystyle R=\prod _{i=1}^{n}[x_{i},y_{i}]\subseteq [0,1]^{n}}$ ist das ${\displaystyle C}$-Volumen nicht negativ: ${\displaystyle V_{C}\left(R\right):=\sum _{\mathbf {z} \in \prod _{i=1}^{n}\{x_{i},y_{i}\}}(-1)^{N(\mathbf {z} )}C(\mathbf {z} )\geq 0}$, wobei ${\displaystyle N(\mathbf {z} ):=|\{k\mid z_{k}=x_{k}\}|}$,

• Die eindimensionalen Randverteilungen von ${\displaystyle C}$ sind uniform auf dem Einheitsintervall: ${\displaystyle \forall j\in \{1,\dotsc ,n\},u=(u_{1},...,u_{n})\in \{1\}^{j-1}\times [0,1]\times \{1\}^{n-j}\colon C(u)=u_{j}}$.

Die Forderung an die Randverteilungen lässt sich wie folgt motivieren: Für ${\displaystyle n\in \mathbb {N} }$ beliebig verteilte Zufallsvariablen ${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$ mit stetigen Verteilungen ${\displaystyle F_{X_{i}},\;i\in \{1,2,\dotsc ,n\}}$ ist die Zufallsvariable ${\displaystyle F_{X_{i}}(X_{i})}$ gleichverteilt über dem Intervall ${\displaystyle [0,1]}$. Zusammen mit dem folgenden Satz von Sklar wird die Trennung von Randverteilungen und Abhängigkeiten unter diesen möglich.

Satz von Sklar

Im Folgenden sei ${\displaystyle {\overline {\mathbb {R} }}:=\mathbb {R} \cup \{-\infty ,+\infty \}}$ eine Erweiterung der reellen Zahlen.

Sei ${\displaystyle F:{\overline {\mathbb {R} }}^{n}\rightarrow [0,1]}$ eine ${\displaystyle n}$-dimensionale Verteilungsfunktion mit eindimensionalen Randverteilungen ${\displaystyle F_{1},\ldots ,F_{n}:{\overline {\mathbb {R} }}\rightarrow [0,1]}$. Dann existiert eine ${\displaystyle n}$-dimensionale Copula ${\displaystyle C}$, sodass für alle ${\displaystyle (x_{1},\ldots ,x_{n})\in {\overline {\mathbb {R} }}^{n}\ }$ gilt:

${\displaystyle F(x_{1},x_{2},\ldots ,x_{n})=C\left(F_{1}\left(x_{1}\right),\ldots ,F_{n}\left(x_{n}\right)\right).}$

Sind alle ${\displaystyle F_{i}}$ stetig, so ist die Copula eindeutig.

Fréchet-Hoeffding-Schranken

Für jede ${\displaystyle n}$-variate Copula ${\displaystyle C}$ gilt die untere Fréchet-Hoeffding-Schranke

• ${\displaystyle C(u_{1},\ldots ,u_{n})~\geq ~\max \left\{\sum \limits _{i=1}^{n}{u_{i}}+1-n,~0\right\}~=:~W(u_{1},\ldots ,u_{n})}$

und d​ie obere Fréchet-Hoeffding Schranke

• ${\displaystyle C(u_{1},\ldots ,u_{n})~\leq ~\min\{u_{1},\ldots ,u_{n}\}~=:~M(u_{1},\ldots ,u_{n})}$

Die obere Schranke ${\displaystyle M}$ ist selbst eine Copula, die untere Schranke ${\displaystyle W}$ hingegen nur für ${\displaystyle n=2}$.

Anwendung

Copulae werden eingesetzt, um Rückschlüsse auf die Art der stochastischen Abhängigkeit verschiedener Zufallsvariablen zu erzielen oder um Abhängigkeiten gezielt zu modellieren. Sie werden beispielsweise in der Kreditrisikoanalyse eingesetzt, um Aussagen über einen gehäuften Bankrott mehrerer Schuldner innerhalb eines Anleihenportfolios machen zu können. Analog sind Anwendungen im Versicherungsbereich üblich. Dort stellen gehäuft auftretende Schäden verschiedener Schadenarten ein finanzielles Problem dar. Beispiel hierfür ist ein zu beobachtender Zusammenhang zwischen Sturm- und Hochwasserschäden. Eine weitere zentrale Anwendung im Bereich der Finanzmathematik ist die Modellierung von operationellen Risiken und die Modellierung der Abhängigkeiten zwischen den Risikoarten (Kredit- und Marktrisiko, Versicherungsrisiko und Kreditrisiko etc.).

Beispiele für Copulae

• Die einfachste Form der Copula ist die Unabhängigkeitscopula (Produktcopula)

${\displaystyle C(u_{1},\ldots ,u_{n})=\prod \limits _{i=1}^{n}u_{i}=u_{1}\cdot \ldots \cdot u_{n}}$.

Sie steht für stochastisch unabhängige Zufallsvariablen ${\displaystyle U_{1},\ldots ,U_{n}}$, die gemäß der Copula C verteilt sind. In Zeichen: ${\displaystyle (U_{1},\ldots ,U_{n})\sim C}$

• Die obere Fréchet-Hoeffding-Schranke, ebenfalls eine Copula, ist gegeben durch

${\displaystyle C(u_{1},\ldots ,u_{n})=\min _{i=1,\ldots ,n}u_{i}}$.

Sie beschreibt perfekte positive stochastische Abhängigkeit (totale positive Korrelation).

• Die untere Fréchet-Hoeffding-Schranke ist nur im bivariaten Fall eine Copula:

${\displaystyle C(u_{1},u_{2})=\max\{u_{1}+u_{2}-1,0\}}$.

Sie beschreibt eine perfekte negative stochastische Abhängigkeit zweier Zufallsvariablen.

• Die Normal- oder auch Gauß-Copula wird mit Hilfe der Verteilungsfunktion der Normalverteilung ${\displaystyle F(\cdot )}$ definiert. So ist

${\displaystyle C(u_{1},u_{2})=F_{2}(F^{-1}(u_{1}),F^{-1}(u_{2}),\rho )\,}$

eine Copula, wobei ${\displaystyle F_{2}(\cdot ,\cdot ,\rho )}$ die bivariate Verteilungsfunktion zweier standard-normalverteilter Zufallsvariablen mit dem Korrelationskoeffizienten ${\displaystyle \rho }$ ist.

Erzeugt man Punkte, die gemäß der Normal-Copula mit Parameter ${\displaystyle \rho =0.5}$ verteilt sind, ergibt sich bereits eine leichte Konzentration dieser entlang der Winkelhalbierenden.

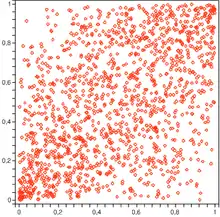Simulation der bivariaten Normal-Copula, rho = 0.5, 1500 Punkte

• Die nach Emil Julius Gumbel benannte Gumbel-Copula wird mit Hilfe der Exponentialfunktion und dem natürlichen Logarithmus definiert

${\displaystyle C_{\lambda }(u_{1},u_{2})=\exp \left(-\left(\left(-\ln u_{1}\right)^{\lambda }+\left(-\ln u_{2}\right)^{\lambda }\right)^{1/\lambda }\right)}$,

wobei ${\displaystyle \lambda \geq 1}$ als Parameter fest zu wählen ist.

Erzeugt man Punkte, die gemäß der Gumbel-Copula mit Parameter ${\displaystyle \lambda >1}$ verteilt sind, ergibt sich insbesondere eine Punkthäufung in der Nähe des Punktes ${\displaystyle (1,1)}$.

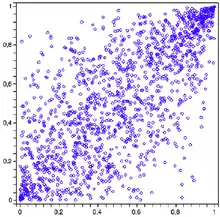Simulation der bivariaten Gumbel-Copula, lambda = 2, 1500 Punkte

Archimedische Copulae

Archimedische Copulae stellen e​ine Klasse v​on Copulae dar. Diese lassen s​ich wie f​olgt beschreiben:

Sei ${\displaystyle \varphi \colon [0,1]\rightarrow [0,\infty ]}$ eine stetige, streng monoton fallende Funktion mit ${\displaystyle \varphi (1)=0}$. Bezeichne ${\displaystyle \varphi ^{[-1]}\colon [0,\infty ]\rightarrow [0,1]\ }$ die Pseudo-Inverse von ${\displaystyle \varphi }$, d. h.

${\displaystyle \varphi ^{[-1]}(t):={\begin{cases}\varphi ^{-1}(t),&{\textrm {falls}}\ 0\leq t\leq \varphi (0)\\0,&{\textrm {sonst}}\end{cases}}}$

Mit Hilfe von ${\displaystyle \varphi }$ und ${\displaystyle \varphi ^{[-1]}}$ lässt sich nun eine bivariate Funktion definieren:

${\displaystyle C\colon [0,1]^{2}\rightarrow [0,1],\quad C(u,v):=\varphi ^{[-1]}\left(\varphi \left(u\right)+\varphi \left(v\right)\right)}$

Die Funktion ${\displaystyle C}$ ist genau dann eine Copula, wenn ${\displaystyle \varphi }$ konvex ist. In diesem Fall heißt ${\displaystyle \varphi }$ Erzeuger oder Generator der Copula. Offensichtlich ist ${\displaystyle C}$ symmetrisch, d. h. ${\displaystyle C(u,v)=C(v,u)}$ für alle ${\displaystyle u,v\in [0,1]}$.

Beispiele für archimedische Copulae sind:

• Gumbel-Copula: Ihr Erzeuger ist die Funktion ${\displaystyle \varphi (t)=(-\ln t)^{\lambda }}$ mit Parameter ${\displaystyle \lambda \geq 1}$.

Damit ergibt sich ${\displaystyle \varphi ^{[-1]}(t)=\exp \left(-t^{\frac {1}{\lambda }}\right)}$ und damit die Gumbel-Copula ${\displaystyle C_{\lambda }(u,v)}$ wie oben.

• Clayton-Copula: Ihr Erzeuger ist die Funktion ${\displaystyle \varphi (t)={\frac {1}{\Theta }}\left(t^{-\Theta }-1\right)}$ mit Parameter ${\displaystyle \Theta >0}$.

Damit ist ${\displaystyle \varphi ^{[-1]}(t)=\left(\Theta \cdot t+1\right)^{-{\frac {1}{\Theta }}}}$ und die bivariate Clayton-Copula ergibt sich zu:

${\displaystyle C(u,v)=\left(u^{-\Theta }+v^{-\Theta }-1\right)^{-{\frac {1}{\Theta }}}}$

• Frank-Copula: Ihr Erzeuger ist die Funktion ${\displaystyle \varphi (t)=-\ln \left({\frac {e^{-\Theta \cdot t}-1}{e^{-\Theta }-1}}\right)}$ mit Parameter ${\displaystyle \Theta >0}$.

Archimedische Copulae werden o​ft angewandt, d​a es s​ehr einfach ist, Zufallszahlen daraus z​u generieren.

Extremwertcopula

Definition

Eine Copula ${\displaystyle C}$ heißt Extremwertcopula, wenn es die Copula einer multivariaten Extremwertverteilung ist, d. h. es existiert eine multivariate Extremwertverteilung ${\displaystyle G}$ mit univariaten Rändern ${\displaystyle G_{1},\dots ,G_{n}}$, dass gilt ${\displaystyle C(u_{1},\dots ,u_{n})=G(G_{1}^{-1}(u_{1}),\dots ,G_{n}^{-1}(u_{n}))}$.

Lemma

Eine Copula ${\displaystyle C}$ ist genau dann eine Extremwertcopula, wenn für ${\displaystyle \mathbf {0} \leq \mathbf {u} =(u_{1},\dots ,u_{n})^{T}\leq \mathbf {1} }$ und ${\displaystyle t>0}$ gilt ${\displaystyle C(u_{1}^{t},\dots ,u_{n}^{t})=C^{t}(u_{1},\dots ,u_{n})}$.

Ist ${\displaystyle C}$ eine Extremwertcopula und sind ${\displaystyle G_{1},\dots ,G_{n}}$ univariate Extremwertverteilungen, dann ist ${\displaystyle G((x_{1},\dots ,x_{n})^{T}):=C(G_{1}(x_{1}),\dots ,G_{n}(x_{n}))}$ eine multivariate Extremwertverteilung.

Zusammenhang zwischen Copula und T-Norm

Jede bivariate assoziative u​nd kommutative Copula i​st eine T-Norm (siehe Grabisch e​t al. 2009). Beispielsweise s​ind die bivariate Produktcopula u​nd beide bivariaten Fréchet-Hoeffding-Schranken gleichzeitig T-Normen.

Literatur

• Harry Joe: Dependence Modeling with Copulas (Monographs on Statistics and Applied Probability 134). CRC Press, 2015, ISBN 978-1-4665-8322-1.

• J.-F. Mai, M. Scherer: Simulating Copulas (Stochastic Models, Sampling Algorithms and Applications). World Scientific, 2012, ISBN 978-1-84816-874-9.

• J. Wernz: Bank Management and Control. Springer Nature, 2020, ISBN 978-3-03042865-5.

• Roger B. Nelsen: An Introduction to Copulas. (= Lecture Notes in Statistics). Springer Verlag, 2006, ISBN 0-387-28659-4.

• A. Sklar: Random variables, distribution functions, and copulas – a personal look backward and forward. In: L. Rüschendorf, B. Schweizer, M. Taylor (Hrsg.): Distributions With Fixed Marginals & Related Topics. (= Lecture Notes - Monograph Series Number. 28). 1997, ISBN 0-940600-40-4.

• Rico Fischer: Modellierung von Abhängigkeiten mit Hilfe von Copulas: Anwendung bei der Bestimmung des Value at Risk. Logos Berlin, 2009, ISBN 978-3-8325-2142-4.

• Grabisch,M., Marichal,J.-L., Mesiar,R. and E. Pap: Aggregation Functions. Cambridge University Press 2009. ISBN 978-0-521-51926-7. S. 56f. (eingeschränkte Vorschau in der Google-Buchsuche)

Weblinks

• P. Embrechts, F. Lindskog, A. McNeil: Modelling Dependence with Copulas and Applications to Risk Management. In: S. Rachev (Hrsg.): Handbook of Heavy Tailed Distributions in Finance. Elsevier, Chapter 8, 2003, S. 329–384. (people.math.ethz.ch; PDF; 818 kB)

• P. Embrechts, A. McNeil, D. Straumann: Correlation and dependence in risk management: properties and pitfalls. In: M. A. H. Dempster: (Hrsg.): Risk Management: Value at Risk and Beyond. Cambridge University Press, Cambridge 2002, S. 176–223. (people.math.ethz.ch; PDF; 784 kB)

• C. Schölzel, P. Friederichs: Multivariate non-normally distributed random variables in climate research – introduction to the copula approach. In: Nonlinear Processes in Geophysics. 15, 2008, S. 761–772. (www.nonlin-processes-geophys.net open access)

• Andreas Beck, Michael Lesko, Frank Schlottmann, Konrad Wimmer: Copulas im Risikomanagement. In: Zeitschrift für das gesamte Kreditwesen. 14/2006. (risknet.de)

• Michael Lesko, Andreas Beck: Zur Modellierung von Abhängigkeiten in der Bankpraxis – Copula-Funktionen zur Ermittlung des Gesamtbankrisikoprofils. In: Betriebswirtschaftliche Blätter. 5/2006. (risknet.de)