Carolyn Gordon

Carolyn Sue Gordon (* 26. Dezember 1950 in Charleston, West Virginia) ist eine US-amerikanische Mathematikerin, die sich mit Differentialgeometrie beschäftigt. Sie ist insbesondere für Beiträge zur inversen Spektraltheorie bekannt.

Wissenschaftlicher Werdegang

Gordon studierte Mathematik an der Purdue University und wurde 1979 an der Washington University bei Edward Nathan Wilson über Isometriegruppen homogener Mannigfaltigkeiten promoviert. Danach war sie als Lady Davis Fellow am Technion in Haifa, war an der Lehigh University und der Washington University, bevor sie 1992 zum Dartmouth College ging, wo sie Professorin für Mathematik ist.

2003 bis 2005 war sie Präsidentin der Association for Women in Mathematics.

Werk

Gordon befasste sich mit riemannscher Geometrie, und dort speziell mit spektralen Problemen (das heißt zu den Eigenwerten, dem Spektrum, des Laplace-Operators auf riemannschen Mannigfaltigkeiten), mit der Geometrie der Lie-Gruppen und symmetrischen Räumen und mit Kähler- und symplektischen Strukturen auf Mannigfaltigkeiten.

Sie wurde bekannt, als sie mit Scott Wolpert und David Webb ein Beispiel zweier einfach zusammenhängender zweidimensionaler Mannigfaltigkeiten gab[1], die zwar das gleiche Schallspektrum (was mathematisch dem Spektrum des Laplace-Operators auf diesen Flächen entspricht) haben, aber verschiedene Form (isospektrale Mannigfaltigkeiten)[2]. Damit beantworteten sie eine berühmte Frage von Mark Kac[3] von 1966 negativ, ob man die Form einer Trommel hören könne (Can one hear the shape of a drum?). Dass dies in mehr als zwei Dimensionen nicht möglich war, war schon vorher bekannt[4], die Frage in zwei Dimensionen (dem eigentlichen Ziel der Frage von Kac) aber offen.[5] Sie benutzten dabei eine Konstruktion von Toshikazu Sunada.

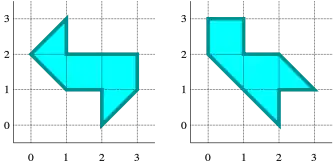
Isospektrale Flächen nach Gordon, Scott, Wolpert

Gordon erweiterte die Beispiele isospektraler Mannigfaltigkeiten später zum Beispiel im hyperbolischen Raum -- zum Beispiel durch Angabe konvexer ebener hyperbolischer Polygone -- oder durch Angabe isospektraler konvexer Körper (ihr erstes Beispiel war nicht konvex) im euklidischen Raum. Sie fand auch geschlossene isospektrale Mannigfaltigkeiten, die lokal nicht isometrisch sind.[6]

Sie ist Mitherausgeberin des Journal of Geometric Analysis.

Auszeichnungen

1990 erhielt sie eine Centennial Fellowship der American Mathematical Society (AMS).
Zusammen mit David Webb erhielt sie den Chauvenet-Preis der Mathematical Association of America (MAA) für You can’t hear the shape of a drum[7].
1999 war sie Invited Speaker auf dem Joint-Meeting der AMS und der MAA.
2010 war sie Noether Lecturer.
Sie ist Fellow der American Mathematical Society.

Weblinks

Commons: Carolyn S. Gordon – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Gordon, Webb, Wolpert One cannot hear the shape of a drum, Bulletin AMS, Band 27, 1992, S. 134–138 (Online), Isospectral plane domains and surfaces via Riemannian orbifolds, Inventiones Mathematicae, Band 110, 1992, S. 1–22
Genauer wird bei berandeten Mannigfaltigkeiten nach Dirichlet- und Neumann Randbedingungen unterschieden, wobei in der Frage nach dem Schallspektrum Dirichlet-Randbedingungen gemeint sind (die Funktion verschwindet auf dem Rand), Gordon bewiesen dies allerdings auch für Neumann Randbedingungen (erste Ableitung verschwindet auf dem Rand). Verschiedene Form wird mathematisch als die Frage danach formuliert, ob sie isometrisch sind.
Kac schreibt das Problem Salomon Bochner zu, machte es aber in seinem Aufsatz populär. Im Ansatz geht es auch auf die Arbeiten von Hermann Weyl Anfang des 20. Jahrhunderts zurück, der zeigte, dass das Volumen aus dem Spektrum bestimmt wird.
John Milnor wies zuerst 1964 (Proc. Nat. Acad. Sci., Band 51, 542) darauf hin, dass zwei isospektrale Tori in 16 Dimensionen aus einem Satz von Ernst Witt konstruiert werden konnten. Weitere Beispiele stammten von Peter Buser, Marie-France Vignéras, Robert Brooks, Gordon selbst und anderen.
Weitere Beispiele in zwei Dimensionen geben zum Beispiel Buser, John Conway, Doyle, Semmler.
Isospectral closed Riemannian manifolds which are not locally isometric, Teil 2, Contemporary Mathematics, Band 173, 1994, S. 121–131
American Scientist, Band 84, Januar/Februar 1996, S. 46–55

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Gordon, Webb, Wolpert One cannot hear the shape of a drum, Bulletin AMS, Band 27, 1992, S. 134–138 (Online), Isospectral plane domains and surfaces via Riemannian orbifolds, Inventiones Mathematicae, Band 110, 1992, S. 1–22

[2] Genauer wird bei berandeten Mannigfaltigkeiten nach Dirichlet- und Neumann Randbedingungen unterschieden, wobei in der Frage nach dem Schallspektrum Dirichlet-Randbedingungen gemeint sind (die Funktion verschwindet auf dem Rand), Gordon bewiesen dies allerdings auch für Neumann Randbedingungen (erste Ableitung verschwindet auf dem Rand). Verschiedene Form wird mathematisch als die Frage danach formuliert, ob sie isometrisch sind.

[3] Kac schreibt das Problem Salomon Bochner zu, machte es aber in seinem Aufsatz populär. Im Ansatz geht es auch auf die Arbeiten von Hermann Weyl Anfang des 20. Jahrhunderts zurück, der zeigte, dass das Volumen aus dem Spektrum bestimmt wird.

[4] John Milnor wies zuerst 1964 (Proc. Nat. Acad. Sci., Band 51, 542) darauf hin, dass zwei isospektrale Tori in 16 Dimensionen aus einem Satz von Ernst Witt konstruiert werden konnten. Weitere Beispiele stammten von Peter Buser, Marie-France Vignéras, Robert Brooks, Gordon selbst und anderen.

[5] Weitere Beispiele in zwei Dimensionen geben zum Beispiel Buser, John Conway, Doyle, Semmler.

[6] Isospectral closed Riemannian manifolds which are not locally isometric, Teil 2, Contemporary Mathematics, Band 173, 1994, S. 121–131

[7] American Scientist, Band 84, Januar/Februar 1996, S. 46–55