Bootstrapping-Verfahren

Das Bootstrapping-Verfahren oder Bootstrap-Verfahren (selten Münchhausenmethode) ist in der Statistik eine Methode des Resampling. Dabei werden wiederholt Statistiken auf der Grundlage lediglich einer Stichprobe berechnet. Verwendung finden Bootstrap-Methoden, wenn die theoretische Verteilung der interessierenden Statistik nicht bekannt ist. Diese Methode wurde erstmals von Bradley Efron 1979 beschrieben[1] und geht aus Überlegungen zur Verbesserung der Jackknife-Methode hervor[2].

Der Bootstrap ersetzt in der Regel die theoretische Verteilungsfunktion $F$ einer Zufallsvariablen durch die empirische Verteilungsfunktion (relative Summenhäufigkeitsfunktion) ${\hat {F}}$ der Stichprobe $x_{1},\ldots ,x_{n}$ . Es ist daher offensichtlich, dass Bootstrapping nur dann gut funktioniert, wenn die empirische Verteilungsfunktion die tatsächliche Verteilungsfunktion hinreichend gut approximieren kann, was eine gewisse Größe der ursprünglichen Stichprobe voraussetzt. Bootstrapping kann als Monte-Carlo Methode verstanden werden, da es wiederholt zufällige Stichproben einer Verteilung zieht.[3]

Nichtparametrisches Bootstrapping ermöglicht weitestgehend ohne oder mit wenigen Modellannahmen, zuverlässig Verteilungen von Statistiken zu schätzen. Es ist unzuverlässig, falls die zugrundeliegende Verteilung $F$ unendliche Varianz besitzt[4].

Anwendungen

Das Verfahren eignet sich einerseits für deskriptive Kennzahlen wie das arithmetische Mittel oder den Median, aber auch für komplexere Methoden der Inferenzstatistik wie Regressionsmodelle. Durch die Flexibilität des Verfahrens ist es möglich, Standardfehler beliebiger Statistiken zu generieren und somit Inferenzen zu erleichtern.

Bootstrap-Konfidenzbereiche
Bootstrap-Tests
Bootstrap aggregating

Verfahren

Es gibt viele Bootstrap-Verfahren, unter anderem Bayesian Bootstrap, Smooth Bootstrap, Parametric Bootstrap, Residual Bootstrap, Gaussian process regression Bootstrap, Wild Bootstrap, Block Bootstrap.

i.i.d Bootstrap

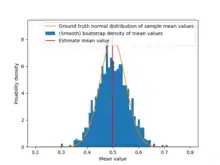
Histogramm der Bootstrap-Mittelwerte (blau)

Für unabhängig und identisch verteilte Zufallsvariablen (i.i.d) werden im einfachsten Fall $B$ Bootstrap-Stichprobenwiederholungen $x_{b}=(x_{1}^{*},\ldots ,x_{n}^{*})\,,b=1,\ldots ,B$ generiert, indem je Ziehung $n$ mal aus der gegebenen Stichprobe ein Wert mit Zurücklegen gezogen wird. Dies entspricht dem wiederholten Ziehen von Zufallszahlen aus der empirischen Verteilungsfunktion ${\hat {F}}$ . Für jede Bootstrap-Stichprobe wird der Wert $T_{b}(x_{1}^{*},\ldots ,x_{n}^{*})=T(x_{b})$ der interessierenden Statistik $T$ berechnet. Die Verteilung von $T(X_{1},\ldots ,X_{n})$ wird schließlich durch die empirische Verteilung der $B$ Werte $T_{b}(x_{1}^{*},\ldots ,x_{n}^{*})$ approximiert. Aus dieser Verteilung der Statistik T kann direkt ein Konfidenzintervall mithilfe der inverse Verteilungsfunktion erzeugt werden.[2]

Block-Bootstrap

Block-Bootstrap[5][6] wird bei zeitlich korrelierten Daten eingesetzt, da i.i.d Bootstrap die zeitliche Korrelation zerstören würde. Beim Block-Bootstrap werden die Daten zunächst in überlappende oder nichtüberlappende, zusammenhängende, Blöcke eingeteilt. Das Signal wird dann z. B. durch Anpassung einer Modellfunktion in einen Trend- und einen Residualanteil aufgeteilt. Nun werden so viele Residualblöcke durch Zurücklegen gezogen und aneinander angehängt, bis die ursprüngliche Länge des Signals erreicht ist. Diese gezogenen Residuuen werden auf die Trendzeitreihe addiert und so wird eine Stichprobenwiederholung erhalten. Dieser Vorgang wird nun oft (z. B. $B=100...1000$ ) wiederholt. Dann kann auf diesen Stichprobenwiederholungen die gewünschte Statistik (Funktion) berechnet werden.

Parametrisches Bootstrap

Beim parametrischen Bootstrap wird angenommen, dass die originale Stichprobe einer bekannten Verteilung mit Parametern $\theta$ folgt. Diese Parameter werden zum Beispiel mithilfe der Maximum-Likelihood-Methode geschätzt, sodass man die Schätzer ${\hat {\theta }}$ erhält. Die geschätzte Verteilungsfunktion ist ${\hat {F}}=F_{\hat {\theta }}$ und aus dieser Verteilung werden wie beim nichtparametrischen Bootstrap wiederholt Stichproben gezogen.

Probleme

In hohen Dimensionen ist Residual-Bootstrap (eine Methode zum Bootstrapen von Regressionsmodellen)[7] sehr anti-konservativ bzw. Pair-Bootstrap sehr konservativ[8].

Bei der Stichprobenwiederholung mit Zurücklegen gilt für eine Stichprobe der Größe $n$ , dass die Wahrscheinlichkeit für ein Sample nicht ausgewählt zu werden $p=1-1/n$ ist. Somit ist bei einer Stichprobenwiederholung mit Zurücklegen die Wahrscheinlichkeit, dass der Wert n mal nicht ausgewählt wird (für große Stichprobenumfänge im Limes) $\lim _{n\to \infty }(1-1/n)^{n}=e^{-1}\approx 0.368=1-0.632$ . Daher enthält eine Stichprobenwiederholung im Schnitt nur 63,2 % der zugrundeliegenden Werte (wobei diese dann auch mehrfach vorliegen dürfen). Dies führt zu Korrekturen wie dem 632 Bootstrap[9].

Die Größe der Bootstrap Stichprobe kann zum Beispiel beim Bootstrapping der Verteilung von Extremwerten Einfluss auf das Ergebnis haben, dort muss die Bootstrap Stichproben-Größe kleiner sein als die originale Stichprobengröße um konsistente Ergebnisse zu erhalten.[10]

Weblinks

Ausgabe des Journals Statistical Science anlässlich des 25-jährigen Jubiläums der Bootstrap-Methode (Statist. Sci. 18(2), Mai 2003)

Literatur

Felix Bittmann: Bootstrapping - An Integrated Approach with Python and Stata. De Gruyter, 2021.
Bradley Efron: Bootstrap Methods: Another Look at the Jackknife. In: The Annals of Statistics. 7, Nr. 1, 1979, S. 1–26. doi:10.1214/aos/1176344552.
Bradley Efron, Robert J. Tibshirani: An introduction to the bootstrap. Chapman & Hall, New York 1993.
Jun Shao, Dongsheng Tu: The Jackknife and Bootstrap. Springer, 1995.

Einzelnachweise

Bradley Efron: Bootstrap Methods: Another Look at the Jackknife. In: The Annals of Statistics. Band 7, Nr. 1, 1. Januar 1979, ISSN 0090-5364, doi:10.1214/aos/1176344552 (projecteuclid.org).
Bradley Efron: Second Thoughts on the Bootstrap. In: Statistical Science. Band 18, Nr. 2, 1. Mai 2003, ISSN 0883-4237, doi:10.1214/ss/1063994968.
William Howard Beasley, Joseph Lee Rodgers: Bootstrapping and Monte Carlo methods. In: APA handbook of research methods in psychology, Vol 2: Research designs: Quantitative, qualitative, neuropsychological, and biological. American Psychological Association, Washington 2012, S. 407–425, doi:10.1037/13620-022.
K. B. Athreya: Bootstrap of the Mean in the Infinite Variance Case. In: The Annals of Statistics. Band 15, Nr. 2, 1. Juni 1987, ISSN 0090-5364, doi:10.1214/aos/1176350371.
Hans R. Kunsch: The Jackknife and the Bootstrap for General Stationary Observations. In: The Annals of Statistics. Band 17, Nr. 3, 1. September 1989, ISSN 0090-5364, doi:10.1214/aos/1176347265.
S. Mignani, R. Rosa: The moving block bootstrap to assess the accuracy of statistical estimates in Ising model simulations. In: Computer Physics Communications. Band 92, Nr. 2-3, Dezember 1995, ISSN 0010-4655, S. 203–213, doi:10.1016/0010-4655(95)00114-7.
Freedman, D. A.: Bootstrapping Regression Models. The Institute of Mathematical Statistics, November 1981.
Noureddine El Karoui, Elizabeth Purdom: Can We Trust the Bootstrap in High-dimensions? The Case of Linear Models. In: Journal of Machine Learning Research. Band 19, Nr. 5, 2018, ISSN 1533-7928, S. 1–66 (jmlr.org [abgerufen am 21. Juli 2021]).
Bradley Efron, Robert Tibshirani: Improvements on Cross-Validation: The 632+ Bootstrap Method. In: Journal of the American Statistical Association. Band 92, Nr. 438, 1. Juni 1997, ISSN 0162-1459, S. 548–560, doi:10.1080/01621459.1997.10474007.
Jaap Geluk, Laurens de Haan: On bootstrap sample size in extreme value theory. In: Publications de l'Institut Mathematique. Band 71, Nr. 85, 2002, ISSN 0350-1302, S. 21–26, doi:10.2298/pim0271021g.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Bradley Efron: Bootstrap Methods: Another Look at the Jackknife. In: The Annals of Statistics. Band 7, Nr. 1, 1. Januar 1979, ISSN 0090-5364, doi:10.1214/aos/1176344552 (projecteuclid.org).

[Efron_2003-2] Bradley Efron: Second Thoughts on the Bootstrap. In: Statistical Science. Band 18, Nr. 2, 1. Mai 2003, ISSN 0883-4237, doi:10.1214/ss/1063994968.

[3] William Howard Beasley, Joseph Lee Rodgers: Bootstrapping and Monte Carlo methods. In: APA handbook of research methods in psychology, Vol 2: Research designs: Quantitative, qualitative, neuropsychological, and biological. American Psychological Association, Washington 2012, S. 407–425, doi:10.1037/13620-022.

[4] K. B. Athreya: Bootstrap of the Mean in the Infinite Variance Case. In: The Annals of Statistics. Band 15, Nr. 2, 1. Juni 1987, ISSN 0090-5364, doi:10.1214/aos/1176350371.

[5] Hans R. Kunsch: The Jackknife and the Bootstrap for General Stationary Observations. In: The Annals of Statistics. Band 17, Nr. 3, 1. September 1989, ISSN 0090-5364, doi:10.1214/aos/1176347265.

[6] S. Mignani, R. Rosa: The moving block bootstrap to assess the accuracy of statistical estimates in Ising model simulations. In: Computer Physics Communications. Band 92, Nr. 2-3, Dezember 1995, ISSN 0010-4655, S. 203–213, doi:10.1016/0010-4655(95)00114-7.

[7] Freedman, D. A.: Bootstrapping Regression Models. The Institute of Mathematical Statistics, November 1981.

[8] Noureddine El Karoui, Elizabeth Purdom: Can We Trust the Bootstrap in High-dimensions? The Case of Linear Models. In: Journal of Machine Learning Research. Band 19, Nr. 5, 2018, ISSN 1533-7928, S. 1–66 (jmlr.org [abgerufen am 21. Juli 2021]).

[9] Bradley Efron, Robert Tibshirani: Improvements on Cross-Validation: The 632+ Bootstrap Method. In: Journal of the American Statistical Association. Band 92, Nr. 438, 1. Juni 1997, ISSN 0162-1459, S. 548–560, doi:10.1080/01621459.1997.10474007.

[10] Jaap Geluk, Laurens de Haan: On bootstrap sample size in extreme value theory. In: Publications de l'Institut Mathematique. Band 71, Nr. 85, 2002, ISSN 0350-1302, S. 21–26, doi:10.2298/pim0271021g.