Eulersche Gerade

Die eulersche Gerade oder Euler-Gerade ist eine spezielle Gerade eines nicht-gleichseitigen Dreiecks. Auf ihr liegen eine Reihe von ausgezeichneten Dreieckspunkten, darunter der Schwerpunkt, der Umkreismittelpunkt, der Höhenschnittpunkt und der Mittelpunkt des Feuerbachkreises. Benannt ist sie nach dem Mathematiker Leonhard Euler. Für das allgemeine Tetraeder im dreidimensionalen Raum gibt es den analogen Begriff (s. u.).

Euler-Gerade e (schwarz),
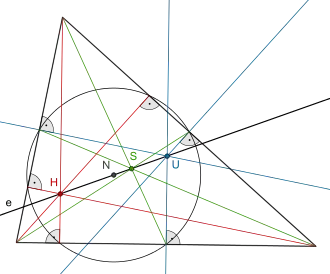
Höhenschnittpunkt H (rot),
Schwerpunkt S (grün, Schnittpunkt der Seitenhalbierenden),
Umkreismittelpunkt U (blau, Schnittpunkt der Mittelsenkrechten),
Feuerbachkreis mit Mittelpunkt N (schwarz)

Eigenschaften

In einem Dreieck liegen der Schwerpunkt S, der Höhenschnittpunkt H und der Umkreismittelpunkt U auf einer gemeinsamen Geraden, der Euler-Geraden. Da der Mittelpunkt des Feuerbachkreises N zugleich der Mittelpunkt der Strecke HU ist (Satz von Feuerbach), liegt dieser ebenfalls auf der Eulergeraden. Darüber hinaus gelten für diese vier Punkte die folgenden Streckenverhältnisse |HU|=3|US|=6|NS|, |HS|=4|NS|, |HN|=3|NS|, |NU|=3|NS| und |SU|=2|NS|.

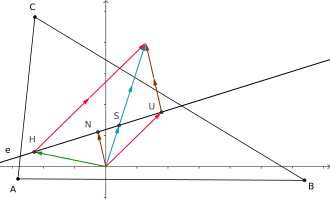
Euler-Gleichung und Feuerbach-Gleichung

Für die Koordinaten der vier Punkte S, H, U und N gelten die folgenden Gleichungen:

$3{\vec {S}}={\vec {H}}+2{\vec {U}}$ (Euler-Gleichung)
$3{\vec {S}}={\vec {U}}+2{\vec {N}}$ (Feuerbach-Gleichung)

In einem gleichschenkligen Dreieck stimmt die eulersche Gerade mit der zur Basis gehörigen Seitenhalbierenden (Mittelsenkrechten, Höhe, Winkelhalbierenden) überein. Im Falle eines gleichseitigen Dreiecks kann man nicht mehr von der eulerschen Geraden sprechen, weil dann die drei bestimmenden Punkte S, U und H zu einem Punkt zusammenfallen. (Sonst könnte ja jede Gerade durch diesen einen Punkt als eulersche Gerade aufgefasst werden, was man aber der Eindeutigkeit halber vermeidet.)

Auf der eulerschen Geraden des Dreiecks ABC liegt auch der Umkreismittelpunkt des Dreiecks, das von den Tangenten an den Umkreis des Dreiecks ABC in den Punkten A, B und C gebildet wird. Darüber hinaus enthält die eulersche Gerade noch weitere ausgezeichnete Punkte des Dreiecks, unter anderem den Longchamps-Punkt, den Schiffler-Punkt und den Exeter-Punkt.

Der Mittelpunkt des Inkreises des Dreiecks liegt auf der eulerschen Gerade genau dann, wenn das Dreieck gleichschenklig ist.[1]

Tetraeder

Euler-Gerade in schwarz

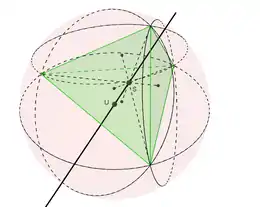
Für ein allgemeines Tetraeder ${\mathcal {T}}\subset \mathbb {R} ^{3}$ nennt man (in Analogie zum zweidimensionalen Fall des Dreiecks) die eulersche Gerade oder Euler-Gerade von ${\mathcal {T}}$ diejenige Gerade $e({\mathcal {T}})\subset \mathbb {R} ^{3}$ , welche den Schwerpunkt $S({\mathcal {T}})$ von ${\mathcal {T}}$ und den Mittelpunkt $U({\mathcal {T}})$ der Umkugel von ${\mathcal {T}}$ verbindet.[2]

Siehe auch

Euler-Gerade in Baryzentrische Koordinaten

Literatur

Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3, S. 162–166
Nathan Altshiller-Court: Modern Pure Solid Geometry. 2. Auflage. Chelsea Publishing Company, Bronx NY 1964, OCLC 1597161.

Weblinks

Eric W. Weisstein: Euler Line. In: MathWorld (englisch).
Heinz Theo Lutstorf: Die Euler-Gerade und ihre ursprüngliche Herleitung. Betrachtungen zu Eulers Urtext - eine Studie in klassischer Algebra. 1. Dezember 2012

Einzelnachweise

Allan L. Edmonds, Mowaffaq Hajja, Horst Martini: Orthocentric Simplices and Biregularity. In: Results in Mathematics. Band 52, Nr. 1-2, August 2008, ISSN 1422-6383, S. 41–50, doi:10.1007/s00025-008-0294-4 (springer.com [abgerufen am 29. August 2019]).
Altshiller-Court, S. 77

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Allan L. Edmonds, Mowaffaq Hajja, Horst Martini: Orthocentric Simplices and Biregularity. In: Results in Mathematics. Band 52, Nr. 1-2, August 2008, ISSN 1422-6383, S. 41–50, doi:10.1007/s00025-008-0294-4 (springer.com [abgerufen am 29. August 2019]).

[2] Altshiller-Court, S. 77