BDF-Verfahren

Die BDF-Verfahren (englisch Backward Differentiation Formulas) s​ind lineare Mehrschrittverfahren z​ur numerischen Lösung v​on Anfangswertproblemen gewöhnlicher Differentialgleichungen:

${\displaystyle y'(x)=f(x,y(x)),\quad y(x_{0})=y_{0},\quad y\colon \mathbb {R} \to \mathbb {R} ^{n}}$.

Dabei wird für ${\displaystyle y(x)}$ eine Näherungslösung an den Zwischenstellen ${\displaystyle x_{i}}$ berechnet:

${\displaystyle y_{i}\approx y(x_{i})\quad i=1,\dotsc ,m}$.

Die Verfahren wurden 1952 v​on Charles Francis Curtiss u​nd Joseph Oakland Hirschfelder eingeführt u​nd sind s​eit dem Erscheinen d​er Arbeiten v​on C. William Gear 1971 a​ls Löser für steife Anfangswertprobleme w​eit verbreitet.

Beschreibung

Im Gegensatz zu Adams-Moulton-Verfahren wird bei BDF-Verfahren nicht die rechte Seite durch ein Interpolationspolynom approximiert, stattdessen konstruiert man ein Polynom ${\displaystyle q_{k}}$ mit (maximalem) Grad ${\displaystyle k}$, welches die letzten ${\displaystyle k}$ Approximationen ${\displaystyle y_{n},\dotsc ,y_{n+k-1}}$ an die Lösung sowie den unbekannten Wert ${\displaystyle y_{n+k}}$ interpoliert:

${\displaystyle q_{k}(x_{i})=y_{i},\quad {\text{für }}i=n,\dots ,n+k}$.

Zusätzlich fordert man, dass das Interpolationspolynom ${\displaystyle q_{k}}$ die gegebene Differentialgleichung im Punkt ${\displaystyle x_{n+k}}$ löst, also dass gilt

${\displaystyle q_{k}'(x_{n+k})=f(x_{n+k},y_{n+k})}$,

und erhält so ein nichtlineares Gleichungssystem für die Bestimmung des implizit gegebenen Wertes ${\displaystyle y_{n+k}}$.

Lagrange-Darstellung

Eine Möglichkeit für die Darstellung des Interpolationspolynoms ${\displaystyle q_{k}}$ ist die Lagrange-Darstellung. Dabei sind die Lagrange-Basispolynome mit den ${\displaystyle k+1}$ Stützstellen ${\displaystyle x_{n},\dots ,x_{n+k}}$ definiert durch

${\displaystyle l_{j}(x_{n+i})=\delta _{ji}={\begin{cases}1&{\text{falls }}j=i,\\0&{\text{falls }}j\neq i.\end{cases}}}$

wobei ${\displaystyle \delta _{ji}}$ das Kronecker-Delta ist. Damit folgt wegen ${\displaystyle q_{k}(x_{n+i})=\sum _{j=0}^{k}l_{j}(x_{n+j})y_{n+j}=y_{n+i}}$ direkt die Darstellung

${\displaystyle q_{k}(x)=\sum _{j=0}^{k}l_{j}(x)y_{n+j}}$.

Mit der Forderung ${\displaystyle q_{k}'(x_{n+k})=f(x_{n+k},y_{n+k})}$ erhält man nun die lineare Rekursionsformel für die BDF-Verfahren:

${\displaystyle \sum _{j=0}^{k}\alpha _{j}y_{n+j}=f(x_{n+k},y_{n+k})}$,

wobei die Koeffizienten ${\displaystyle \alpha _{j}}$ gegeben sind durch

${\displaystyle \alpha _{j}=l_{j}'(x_{n+k}),\quad j=0,\dots ,k}$.

Alternative Lagrange-Darstellung

Alternativ betrachten w​ir die Lagrange-Basispolynome definiert durch

${\displaystyle L_{j}(-s)=\delta _{js}={\begin{cases}1&{\text{falls }}j=s,\\0&{\text{falls }}j\neq s.\end{cases}}}$

Damit f​olgt die Darstellung

${\displaystyle q_{k}(x_{n+k}+sh)=\sum _{j=0}^{k}L_{k-j}(s)y_{n+j}}$.

Dabei ist ${\displaystyle h=x_{i+1}-x_{i}}$ der Abstand der Stützstellen und die konstante Schrittweite des Verfahrens. Mit der Forderung ${\displaystyle q_{k}'(x_{n+k})=f(x_{n+k},y_{n+k})}$, wobei hier

${\displaystyle q_{k}'(x)={\frac {d}{dx}}q_{k}(x)={\frac {d}{d(sh)}}q_{k}(x_{n+k}+sh)={\frac {1}{h}}{\frac {d}{ds}}q_{k}(x_{n+k}+sh)}$

gilt, erhält man nun für die Berechnung der Koeffizienten ${\displaystyle \alpha _{j}}$

${\displaystyle \alpha _{j}=L_{k-j}'(0),\quad j=0,\dots ,k}$

und d​amit die Rekursionsformel

${\displaystyle \sum _{j=0}^{k}L_{k-j}'(0)y_{n+j}=hf(x_{n+k},y_{n+k})}$

Newton-Darstellung

Die Newton-Darstellung des Interpolationspolynoms ${\displaystyle q_{k}}$ verwendet Rückwärtsdifferenzen, welche rekursiv definiert sind durch

${\displaystyle \nabla ^{0}y_{i}=y_{i},\quad \nabla ^{j+1}y_{i}=\nabla ^{j}y_{i}-\nabla ^{j}y_{i-1}.}$

Damit lässt sich ${\displaystyle q_{k}}$ schreiben als

${\displaystyle q_{k}\left(x_{n+k}+sh\right)=\sum _{j=0}^{k}(-1)^{j}{\binom {-s}{j}}\nabla ^{j}y_{n+k}}$.

Diese Formel führt wegen ${\displaystyle \left.{\frac {d}{ds}}(-1)^{j}{\binom {-s}{j}}\right|_{s=0}={\frac {1}{j}}}$ für ${\displaystyle j=1,\dots ,k}$ auf die Darstellung

${\displaystyle \sum \limits _{j=1}^{k}{\frac {1}{j}}\nabla ^{j}y_{n+k}=hf(x_{n+k},y_{n+k})}$

der BDF-Verfahren.

Berechnungsformeln

Alle oben betrachteten Darstellungen der Berechnungsformeln sind äquivalent, da sie nur verschiedene Arten der Darstellung des eindeutigen Interpolationspolynoms ${\displaystyle q_{k}}$ verwendet haben. Für ${\displaystyle k\leq 6}$ lauten die impliziten Berechnungsformeln der BDF(k)-Verfahren:

• BDF(1) – implizites Euler-Verfahren:

${\displaystyle y_{n+1}-y_{n}=hf(x_{n+1},y_{n+1})}$

• BDF(2):

${\displaystyle 3y_{n+2}-4y_{n+1}+y_{n}=2hf(x_{n+2},y_{n+2})}$

• BDF(3):

${\displaystyle 11y_{n+3}-18y_{n+2}+9y_{n+1}-2y_{n}=6hf(x_{n+3},y_{n+3})}$

• BDF(4):

${\displaystyle 25y_{n+4}-48y_{n+3}+36y_{n+2}-16y_{n+1}+3y_{n}=12hf(x_{n+4},y_{n+4})}$

• BDF(5):

${\displaystyle 137y_{n+5}-300y_{n+4}+300y_{n+3}-200y_{n+2}+75y_{n+1}-12y_{n}=60hf(x_{n+5},y_{n+5})}$

• BDF(6):

${\displaystyle 147y_{n+6}-360y_{n+5}+450y_{n+4}-400y_{n+3}+225y_{n+2}-72y_{n+1}+10y_{n}=60hf(x_{n+6},y_{n+6})}$

Eigenschaften

Die BDF-Verfahren sind alle implizit, da der unbekannte Wert ${\displaystyle y_{n+k}}$ in die Gleichung eingeht. BDF(k) besitzt genau die Konsistenzordnung k. Das Verfahren BDF(1) ist das implizite Euler-Verfahren. Dieses und BDF(2) sind A-stabil, die Verfahren höherer Ordnung A(${\displaystyle \alpha }$)-stabil, wobei der Öffnungswinkel ${\displaystyle \alpha }$ sich mit höherer Ordnung verkleinert. Insbesondere BDF(2) ist aufgrund seiner optimalen Eigenschaften bezüglich der zweiten Dahlquist-Barriere bei der Berechnung steifer Differentialgleichungen sehr beliebt. Für k<6 sind die Verfahren stabil und konsistent und damit auch konvergent. Der größte Anreiz der BDF-Verfahren sind ihre großen Stabilitätsgebiete, weshalb sie sich für den Einsatz bei der Lösung von steifen Anfangswertproblemen eignen. Für k>6 sind die Verfahren instabil.

• Stabilitätsgebiete der BDF-Verfahren
• 
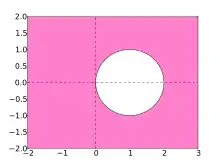  BDF1
• 
  BDF2
• 
  BDF3
• 
  BDF4
• 
  BDF5
• 
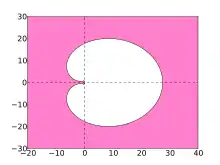  BDF6

Literatur

• E. Hairer, Syvert P. Nørsett, Gerhard Wanner: Solving Ordinary Differential Equations I, Nonstiff Problems, Springer Verlag, ISBN 3-540-56670-8
• E. Hairer, G. Wanner: Solving Ordinary Differential Equations II, Stiff problems, Springer Verlag, ISBN 3-540-60452-9
• H.R. Schwarz, N. Köckler: Numerische Mathematik, Teubner (2004)
• Curtiss, Hirschfelder Integration of stiff equations, Proc. Nat. Acad. Sci. U.S.A., Band 38, 1952, 235–243.

Weblinks

• Gear, Backward Differentiation Formulas, Scholarpedia