A/V-Verhältnis

Das Oberfläche-zu-Volumen-Verhältnis (A/V-Verhältnis) ist der Quotient aus der Oberfläche $A$ und dem Volumen $V$ eines geometrischen Körpers. Es hat die Dimension 1/Länge.

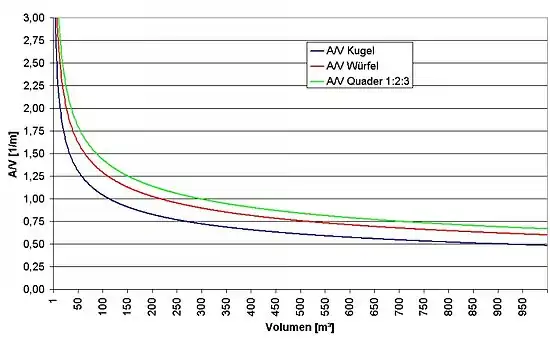
A/V-Verhältnis von Kugel, Würfel und Quader (Seitenverhältnis 1:2:3) bei gleichem Volumen

Bei gegebenem Volumen weist von allen Körpern die Kugel die kleinste Oberfläche auf. Bei wachsendem Volumen nimmt das A/V-Verhältnis bei allen Körpern ab, da die Oberfläche quadratisch, das Volumen jedoch kubisch (in der dritten Potenz) wächst. Das ist von Bedeutung für die Abkühlungsgeschwindigkeit verschieden großer Massen: Die Abkühlung erfolgt proportional zur Größe der Oberfläche, die beim Größerwerden jedoch langsamer wächst als das Volumen, so dass größere Massen langsamer abkühlen als kleine. Das ist auch eine Erklärung dafür, dass Kaiserpinguine in der Antarktis größer sind und somit mehr Wärme behalten als Galápagos-Pinguine nahe dem Äquator, die Wärme eher abgeben wollen (Bergmannsche Regel und Allometrie).[1]

Betrachtung

Allgemein gilt für Körper: wenn man die Kantenlänge eines Quaders verdoppelt, vervierfacht sich seine Fläche (allgemeinsprachlich: Oberfläche; oder auch bei Berücksichtigung von Austauschprozessen, seine Grenzfläche); sein Volumen aber verachtfacht sich. Große Körper haben deshalb eine (z. B. für die Wärmespeicherung) günstigere Relation von Volumen zu Oberfläche:

V_{1}=a\times b\times c

(beim Würfel:

V_{1}=a\times a\times a

)

A_{1}=2\times a\times b+2\times b\times c+2\times a\times c

(Würfel:

A=6\times a\times a

)

V_{2}=2a\times 2b\times 2c=2\times 2\times 2\times a\times b\times c=8\times a\times b\times c

Das gilt auch für den Zylinder: wenn man seinen Durchmesser und seine Höhe verdoppelt, verachtfacht sich sein Volumen. Auch wenn man den Durchmesser einer Kugel verdoppelt, verachtfacht sich ihr Volumen. Eine Kugel hat das größte Verhältnis von Volumen zu Oberfläche aller geometrischen Körper.

Physiologische Implikationen

Der Stoffaustausch einer Zelle erfolgt über deren Oberfläche. Aufnahme und Abgabe von für den Stoffwechsel wichtigen Molekülen vollzieht sich über die Zellmembran (Phasengrenzflächen). Dabei spielt auch das Verhältnis von Zelloberfläche zu Zellvolumen eine wichtige Rolle. Je kleiner eine Zelle (oder auch ein Körper) ist, desto weniger Volumen hat er, im Verhältnis zu seiner Oberfläche. Eine stoffwechselaktive Zelle ist deshalb meist klein, da bei einem kleinen Zellkörper das Verhältnis von Oberfläche zu Volumen günstiger ist als bei großvolumigen Zellen. Soll nun aber eine Zelle aufgrund des evolutionären Drucks sowohl großvolumig als auch stoffwechselaktiv sein ist dies nur durch eine zusätzliche Vergrößerung der Oberfläche durch Falten oder Ausstülpungen möglich, als Beispiel sei hier der Osteoklast angeführt.[2]

Bei verschiedengroßen Organismen führt das Verhältnis von Oberfläche zu Volumen zu ökogeographischen Beobachtungen wie beispielsweise der Bergmannschen Regel.

Bauphysik

In der Bauphysik und beim Wärmeschutznachweis ist das A/V-Verhältnis eine wichtige Kenngröße für die Kompaktheit eines Gebäudes. Es berechnet sich als der Quotient aus der wärmeübertragenden Hüllfläche, d. h. Flächen, die Wärme an die Umwelt abgeben, wie Wände, Fenster, Dach, und dem beheizten Gebäudevolumen. Das A/V-Verhältnis beeinflusst entscheidend den Heizenergiebedarf. Ein geringeres A/V-Verhältnis bedeutet bei gleichem Gebäudevolumen eine kleinere Wärme übertragende Außenfläche. Pro m³ Volumen ist somit weniger Energie notwendig, um die Wärmeverluste über die Hülle auszugleichen.

Große Gebäude weisen naturgemäß kleinere A/V-Verhältnisse auf, als z. B. Einfamilienhäuser. Typische Werte für Einfamilienhäuser liegen zwischen 0,8 und 1,0 ${\textstyle \mathrm {\frac {1}{m}} }$ . Bei großen, kompakten Gebäuden sind Werte bis unter 0,2 ${\textstyle \mathrm {\frac {1}{m}} }$ möglich.

Beispiele

Körper	Länge $a$	Oberfläche	Volumen	A/V-Verhältnis	A/V-Verhältnis pro Raumeinheit
Tetraeder	Seite	${\sqrt {3}}a^{2}$	${\frac {{\sqrt {2}}a^{3}}{12}}$	${\frac {6{\sqrt {6}}}{a}}\approx {\frac {14{,}697}{a}}$	7,21
Würfel	Seite	$6a^{2}$	$a^{3}$	${\frac {6}{a}}$	6
Oktaeder	Seite	$2{\sqrt {3}}a^{2}$	${\frac {1}{3}}{\sqrt {2}}a^{3}$	${\frac {3{\sqrt {6}}}{a}}\approx {\frac {7{,}348}{a}}$	5,72
Dodekaeder	Seite	$3{\sqrt {25+10{\sqrt {5}}}}a^{2}$	${\frac {1}{4}}(15+7{\sqrt {5}})a^{3}$	${\frac {12{\sqrt {25+10{\sqrt {5}}}}}{(15+7{\sqrt {5}})a}}\approx {\frac {2{,}694}{a}}$	5,31
Ikosaeder	Seite	$5{\sqrt {3}}a^{2}$	${\frac {5}{12}}(3+{\sqrt {5}})a^{3}$	${\frac {12{\sqrt {3}}}{(3+{\sqrt {5}})a}}\approx {\frac {3{,}970}{a}}$	5,148
Kugel	Radius	$4\pi r^{2}$	${\frac {4\pi r^{3}}{3}}$	${\frac {3}{r}}$	4,836

Einzelnachweise

Hans Joachim Schlichting; Bernd Rodewald: Von großen und kleinen Tieren. In: Praxis der Naturwissenschaften – Physik. 37/5, 2 (1988).
Werner Buselmaier: Biologie für Mediziner. 12. Auflage. Springer, 2012, ISBN 978-3-642-27174-8, S. 4 f.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Hans Joachim Schlichting; Bernd Rodewald: Von großen und kleinen Tieren. In: Praxis der Naturwissenschaften – Physik. 37/5, 2 (1988).

[2] Werner Buselmaier: Biologie für Mediziner. 12. Auflage. Springer, 2012, ISBN 978-3-642-27174-8, S. 4 f.