Wurzelschnecke

Die Wurzelschnecke, Wurzelspirale oder Spirale des Theodorus (nach Theodoros von Kyrene (5. Jh. v. Chr.)) ist eine Spirale, die von rechtwinkligen Dreiecken mit Seitenlängen 1, ${\sqrt {n}}$ und ${\sqrt {n+1}}$ erzeugt wird.

Die Spirale bis

{\sqrt {17}}

Die ersten drei Windungen

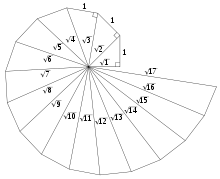
Konstruktion und Eigenschaften

Das erste Dreieck hat also die Seitenlängen 1, ${\sqrt {1}}$ und ${\sqrt {2}}$ . Auf der Hypotenuse dieses Dreiecks wird das rechtwinklige Dreieck mit den Seitenlängen 1, ${\sqrt {2}}$ und ${\sqrt {3}}$ errichtet usw. Die aneinandergrenzenden Katheten bilden dann eine Spirale.

Im Gegensatz zur Archimedischen oder Logarithmischen Spirale besteht die Wurzelschnecke aus Geradenstücken. Sie ist damit als Kurve nicht differenzierbar, lässt sich aber dafür exakt durch die abzählbar vielen Eckpunkte beschreiben.

1958 bewies Erich Teuffel, dass sich niemals zwei der Hypotenusen decken werden, egal, wie weit man die Spirale zeichnet.[1]

Die kleinste Anzahl von Dreiecken, die die k-te Drehung der Spirale vollendet, findet sich in der On-Line Encyclopedia of Integer Sequences.[2] Die ersten Folgeglieder sind 17, 54, 110, 186, …

Verwendung

Mit Hilfe der Wurzelschnecke lassen sich die Quadratwurzeln von positiven Ganzzahlen geometrisch konstruieren.

Es wird angenommen, dass Theodoros mit Hilfe der Wurzelschnecke bewies, dass die Wurzeln der nicht quadratischen Ganzzahlen von 3 bis 17 irrationale Zahlen sind. (Dass die Wurzel aus 2 irrational ist, war schon lange vor Theodoros bekannt.)[3]

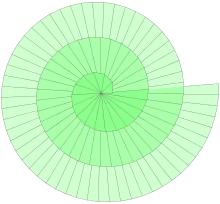
Zusammenhang mit der Archimedischen Spirale

Mit wachsender Windungszahl nähert sich die Wurzelschnecke asymptotisch einer Archimedischen Spirale an.

Der Spiralabstand nähert sich somit mit zunehmender Windungszahl der Zahl $\pi$ an.[4]

Windungsnummer:	Berechneter durchschnittlicher Windungsabstand	Genauigkeit des durchschnittlichen Windungsabstandes im Vergleich zu $\pi$
2	3.1592037	99.44255%
3	3.1443455	99.91245%
4	3.14428	99.91453%
5	3.142395	99.97447%
→ ∞	→ $\pi$	→ 100%

Literatur

Detlef Gronau: The Spiral of Theodorus. The American Mathematical Monthly, Vol. 111, No. 3 (März, 2004), S. 230–237 (JSTOR 4145130)
James Tanton: Mathematics Galore! MAA, 2012, ISBN 978-0-88385-776-2, S. 8–9
Julian Havil: The Irrationals. Princeton University Press, 2012, ISBN 978-0-691-14342-2, S. 7, 272–274
Paul J. Nahin: An Imaginary Tale: The Story of √-1. Princeton University Press, 2012, ISBN 978-1-4008-3389-4, S. 33–34

Weblinks

Commons: Wurzelschnecke – Sammlung von Bildern, Videos und Audiodateien

Wurzelspirale

Einzelnachweise

Erich Teuffel: Eine Eigenschaft der Quadratwurzelschnecke. In: Math.-Phys. Semesterber. 6 (1958), S. 148–152.
http://oeis.org/A072895
Paul J. Nahin: An Imaginary Tale: The Story of √-1. Princeton University Press, 2012, ISBN 978-1-4008-3389-4, S. 33–34
http://kociemba.org/themen/spirale/spirale.htm

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Erich Teuffel: Eine Eigenschaft der Quadratwurzelschnecke. In: Math.-Phys. Semesterber. 6 (1958), S. 148–152.

[2] ttp://oeis.org/A072895

[3] Paul J. Nahin: An Imaginary Tale: The Story of √-1. Princeton University Press, 2012, ISBN 978-1-4008-3389-4, S. 33–34

[4] ttp://kociemba.org/themen/spirale/spirale.htm