Vorwärtsinduktion
Die Aufgabe der Vorwärtsinduktion in der Spieltheorie ist es, für rationale Spieler die optimalen Strategien in einem Spiel mit aufeinanderfolgenden Zügen herauszufinden. Um das Spiel besser darzustellen, betrachtet man den sogenannten Spielbaum und analysiert das Spiel von seinem Beginn bis zum Ende, d. h. man arbeitet sich „vorwärts“ durch den Baum. Somit steht die Vorwärtsinduktion im Gegensatz zu der Rückwärtsinduktion[1], bei der die vorherigen Spielzüge analysiert werden, um die besten Optionen für die Spieler zu finden.
Beispiel I
Tabelle
| Sp.1(Mann) / Sp.2(Frau) | Kino | Theater |
|---|---|---|
| Kino | 1,3 | 0,0 |
| Theater | 0,0 | 3,1 |
Spielablauf
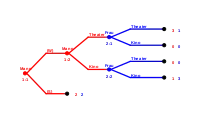
Das Spiel wird wie folgt gespielt: Spieler 1 (Mann) erhält am Anfang eine sogenannte Außenoption. Er kann sich entscheiden, ob er an dem Spiel teilnehmen möchte - Strategie (W)- oder an dem Spiel nicht teilnehmen möchte - Strategie (S). Entscheidet er sich dafür, das Spiel zu beenden (S), so erhalten beide Spieler die Auszahlung 2. Nimmt er dagegen an dem Spiel teil, wird weiter ein Kampf-der-Geschlechter-Spiel gespielt. Bei diesem Spiel wollen sich die Spieler koordinieren, indem sie jeweils die gleiche Aktion - (Kino,Kino) oder (Theater,Theater) durchführen. So erhalten sie eine höhere Auszahlung als im Falle unterschiedlicher Verhaltensweise, in dem sie nur eine Auszahlung von Null erhalten.
Für den Mann, der rational handelt, wäre es sinnvoll, das Spiel fortzusetzen, wenn er eine höhere Auszahlung als 2 erhalten kann. Die Auszahlung von 2 kann er sich sofort garantieren, indem er die Strategie (S) spielt und das Spiel beendet. Eine höhere Auszahlung als 2 bekommt er nur, wenn er im Teilspiel die Strategie (Theater) spielt. Denn, wenn er (Kino) spielt, bekommt er nur eine Auszahlung von 1.
Für die Frau wäre die optimale Strategie auch (Theater), weil sie weiß, dass der Mann rational handelt und im Teilspiel auch die Strategie (Theater) spielt. So bekommt sie zumindest eine Auszahlung von 1, statt einer Auszahlung von 0 (wenn sie die Strategie (Kino) gespielt hätte).
Fazit:
Wird ein Knoten erreicht, der möglicherweise außerhalb des Gleichgewicht-Pfades liegt, dann sollte der an diesem Knoten entscheidende Spieler sich überlegen, welche Aktionen der andere Spieler stattdessen gewählt haben könnte, aber nicht gewählt hat. Dann sollte er vorwärts schauen und überlegen, welche Strategie der andere Spieler im weiteren Spielverlauf zu wählen plant. Die Spieler sollten also vorwärts - vom Beginn zum Ende des Baums denken, und eine Abweichung eines Spielers vom Gleichgewicht-Pfad sollte interpretiert werden als Signal dafür, wie dieser Spieler in Zukunft zu entscheiden plant.[2][3]
Gleichgewichte
Das Teilspiel (Koordinationsspiel) hat folgende Nash-Gleichgewichte
1 (Kino,Kino) - Spieler 1 spielt (Kino) und Spieler 2 spielt (Kino)
2.(Theater,Theater) - Spieler 1 spielt (Theater) und Spieler 2 spielt (Theater)
Die beiden Spieler hier präferieren ein Gleichgewicht gegenüber einem Nicht-Gleichgewicht. Die Präferenzen bezüglich der beiden Gleichgewichte können allerdings unterschiedlich sein, müssen aber nicht.
Ein teilspielperfektes Gleichgewicht des modifizierten Spiels (mit Außenoption) ist, dass der Mann (S) und (Kino) und die Frau (Kino) spielt. Da aber (Kino,Kino) ein Nash-Gleichgewicht des Teilspiels ist und der Mann in diesem Nash-Gleichgewicht eine Auszahlung von nur 1 erwartet, wird er im ersten Zug die Strategie (S) spielen, um die Auszahlung 2 zu erhalten.
Beispiel II
Es wird das folgende Spiel betrachtet:
Bimatrix
| Spieler 1 / Spieler 2 | A2 | (B2,C2) | (B2,D2) |
|---|---|---|---|
| A1 | 9,9 | 9,9 | 9,9 |
| (B1,C1) | 9,9 | 10,1 | 0,0 |
| (B1,D1) | 9,9 | 0,0 | 1,10 |
Spielablauf
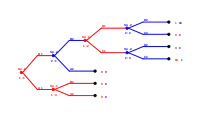
Für dieses Beispiel besagt die Logik der Vorwärtsinduktion, dass man den Verzicht auf Ai , i=(1,2) so zu interpretieren hat, dass in dem auf (B1,B2) folgenden Teilspiel Spieler i mehr als 9 verdienen will. Also wird Spieler 1 nicht (D1) spielen und Spieler 2 wird nicht (C2) wählen, weil so die beiden Spieler nur eine Auszahlung von maximal 1 erhalten werden. Dass dies natürlich für die beiden Spieler so zu interpretieren wäre, weist darauf hin, dass solche Interpretationen manchmal absurd sein können. Nach den Zügen (B1) und (B2) sind solche Ansprüche an das Verhalten im Teilspiel inkonsistent und sollten revidiert werden.[4]
Gleichgewichte
In diesem Beispiel sind die Strategien (B1,D1) durch A1 und die Strategien (B2,C2) durch A2 schwach dominiert und werden daher mit Wahrscheinlichkeit von Null verwendet. Im nach der Zugfolge (B1,B2) folgenden Teilspiel wird die Strategie (C1,D2) verfolgt, die aber zu keinem Gleichgewicht des Teilspiels führt.
Vorwärtsinduktion vs. Rückwärtsinduktion
Die Spieltheorie beschreibt optimierendes Verhalten in einer interaktiven Situation durch Gleichgewichtskonzepte.
Bei der Vorwärtsinduktion kann man durch Aktionen sein Vorhaben mitteilen - wie man gedenkt, im Folgenden zu spielen. Das Spiel wird von Beginn bis zum Ende des Spielbaums analysiert, man arbeitet sich also “vorwärts”. So kann man durch die Vorwärtsinduktion ein Gleichgewichtskonzept wie teilspielperfektes Gleichgewicht ausschließen.
Im Unterschied zu der Vorwärtsinduktion beginnt die Analyse des Spiels bei der Rückwärtsinduktion am unteren Ende des Spielbaums, d. h. an den Entscheidungsknoten, an denen der letzte Spieler am Zug ist. An jedem dieser Knoten wird die beste Antwort dieses Spielers bestimmt. So arbeitet man sich “rückwärts” durch den Baum. Diese Prozedur wird solange wiederholt, bis die optimalen Strategien aller Spieler an jedem Knoten gefunden sind.
Mit Hilfe der Rückwärtsinduktion kann ein Gleichgewichtskonzept wie das teilspielperfekte Gleichgewicht im Falle eines Extensivformspiels mit vollkommener Information gefunden werden. Das teilspielperfekte Gleichgewicht stellt eine Verallgemeinerung des Prinzips der Rückwärtsinduktion dar. Hier wird ein rationales Verhalten im Sinne des Nash-Gleichgewichts nicht nur für den gesamten Spielbaum gefordert, sondern auch für alle Teilspiele. Das sind alle Teilbereiche des Spielbaums, die selbst wieder die Struktur eines Spielbaums haben. Das unglaubwürdige Verhalten wird bei der Rückwärtsinduktion auch an den Entscheidungsknoten eliminiert, die im Verlauf des Spiels nicht erreicht werden können.[5]
Literatur
- D. Fudenberg, Jean Tirole: Game Theory. MIT Press, 1991.
- Gernot Sieg: Spieltheorie. Oldenbourg Verlag, München 2005.
- Siegfried K. Berninghaus, Karl-Martin Ehrhart, Werner Güth: Strategische Spiele: Eine Einführung in die Spieltheorie. Springer, Berlin/Heidelberg 2006.
- David. M. Kreps, Robert Wilson: Reputation and Imperfect Information. In: Journal of Economic. Theory, vol. 27, 1982.
Einzelnachweise
- http://wikiludia.mathematik.uni-muenchen.de/wiki/index.php?title=R%C3%BCckw%C3%A4rtsinduktion
- Gernot Sieg: Spieltheorie. Oldenbourg Verlag, München 2005, S. 112–113
- D. Fudenberg, Jean Tirole: Game Theory. MIT Press, 1991. S. 460–463
- Siegfried K. Berninghaus, Karl-Martin Ehrhart, Werner Güth: Strategische Spiele: Eine Einführung in die Spieltheorie. Springer, Berlin/Heidelberg 2006. S. 141–143
- David M. Kreps, Robert Wilson: Reputation and Imperfect Information. In: Journal of Economic. Theory, vol. 27, 1982