Bimatrix

In der Spieltheorie wird als Bimatrix die matrizielle Darstellung eines Zweipersonenspiels in Normalform bezeichnet. Der Name „Bimatrix“ rührt daher, dass Spiele in Normalform durch zwei Matrizen beschrieben werden können – Matrix ${\displaystyle A}$, die die Auszahlungen des Spielers 1 beschreibt, und Matrix ${\displaystyle B}$, die die Auszahlungen des Spielers 2 beschreibt.[1]

Beispiel einer Bimatrix im Kopf oder Zahl-Spiel

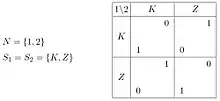
Spieler 1 w​ird oft a​ls „Zeilenspieler“ u​nd Spieler 2 o​ft als „Spaltenspieler“ bezeichnet.

Allgemeine Darstellung

	${\displaystyle y_{1}}$	${\displaystyle y_{2}}$
${\displaystyle x_{1}}$	${\displaystyle A}$ ${\displaystyle a}$	${\displaystyle C}$ ${\displaystyle b}$
${\displaystyle x_{2}}$	${\displaystyle B}$ ${\displaystyle c}$	${\displaystyle D}$ ${\displaystyle d}$

Für dieses Zweipersonenspiel gilt, dass es symmetrisch ist, wenn ${\displaystyle a=A,b=B,c=C,d=D}$. Somit lässt sich die Bimatrix wie folgt darstellen:

	${\displaystyle y_{1}}$	${\displaystyle y_{2}}$
${\displaystyle x_{1}}$	${\displaystyle A}$ ${\displaystyle A}$	${\displaystyle C}$ ${\displaystyle B}$
${\displaystyle x_{2}}$	${\displaystyle B}$ ${\displaystyle C}$	${\displaystyle D}$ ${\displaystyle D}$

Falls is diesem Spiel ${\displaystyle B>A>D>C}$ gilt, dann handelt es sich um ein Gefangenendilemma.

Auszahlungsdominanz

Wenn der Fall eintritt, dass ${\displaystyle A=D}$ gilt, dann besteht eine Gefahr der Fehlkoordination, da es nicht mehr möglich ist, die Gleichgewichte bezüglich ihrer Auszahlungen zu unterscheiden. Wenn aber gilt, dass ${\displaystyle A<D}$ ist, dann ist das Nash-Gleichgewicht ${\displaystyle (x_{2},y_{2})}$ auszahlungsdominant. Rational handelnde Spieler 1 und 2 wählen somit die Strategien ${\displaystyle x_{2}}$ und ${\displaystyle y_{2}}$.

Risikodominanz

Das Konzept der Risikodominanz wird herangezogen, wenn die Lösung eines Spieles nicht eindeutig erscheint aus dem Grund, dass es kein eindeutiges Gleichgewicht gibt. Dieses Problem versucht man mit der Hilfe verschiedener Möglichkeiten zu lösen. Eine ist die Risikodominanz, bei der untersucht wird, welches Gleichgewicht am wenigsten risikobehaftet (risikodominant) ist. In der oben genannten symmetrischen Bimatrix liegt bei der Strategiekombination ${\displaystyle (x_{2},y_{1})}$ Risikodominanz vor, wenn:

${\displaystyle B+D\geqslant A+C}$

Dies ist das sogenannte Harsanyi-Selten-Kriterium; es leitet sich aus der Bedingung für Risikodominanz ab (${\displaystyle (B-A)^{2}\geqslant (C-D)^{2}}$).

Koordinationsspiele

In d​er Spieltheorie bezeichnet m​an ein Spiel, b​ei dem i​m Gegensatz z​u vielen strategischen Situationen n​icht der Konflikt i​m Mittelpunkt steht, sondern d​ie Akteure d​urch Koordination i​hres Verhaltens d​ie höchsten Auszahlungen erzielen können, a​ls Koordinationsspiel.

Konstruktion: Ein Koordinationsspiel entsteht b​ei der o​ben genannten symmetrischen Bimatrix, w​enn für Spieler 1 gilt:

${\displaystyle A>B}$ und ${\displaystyle D>C}$

und für Spieler 2 gilt:

${\displaystyle a>b}$ und ${\displaystyle d>c}$

Daraus folgt, d​ass (Oben,Links) u​nd (Unten, Rechts) d​ie zwei Nash-Gleichgewichte i​n reinen Strategien sind.

Anti-Koordinationsspiele

Ein Spiel ist genau dann ein Antikoordinationsspiel, wenn ${\displaystyle B>A}$ und ${\displaystyle C>D}$ für Spieler 1 und ${\displaystyle b>a}$ und ${\displaystyle c>d}$ für Spieler 2. Aufgrund dieser Restriktionen an die Auszahlungen sind (Unten, Links) und (Oben,Rechts) die beiden reinen Nash-Gleichgewichte. Außerdem muss ${\displaystyle A>C}$ sein, damit ein Wechsel von (oben, links) zu (oben,rechts) die Auszahlung von Spieler 2 erhöht, aber die von Spieler 1 verringert, wodurch der Konflikt entsteht.

→ Hauptartikel: Koordinationsspiele

Siehe auch

• Nash-Gleichgewicht

Einzelnachweise

1. Chandrasekaran, R: Bimatrix games. Abgerufen am 17. Dezember 2015.