Volatilitäts-Smile
Unter Volatilitäts-Smile (auch Volatilitätslächeln, englisch smile bedeutet ‚lächeln‘) wird in den Wirtschaftswissenschaften der Zusammenhang verstanden, dass die implizite Volatilität – dies ist jene, die nach dem Black-Scholes-Modell vorliegen muss, damit der aktuelle Marktpreis einer Option zustande kommt – umso niedriger ist, je mehr die Option „am Geld“ ist.
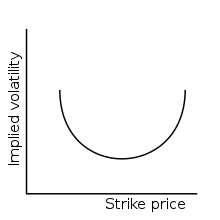
Häufig, insbesondere bei Devisenoptionen, steigt die implizite Volatilität sowohl bei Ausübungspreisen unterhalb als auch oberhalb des aktuellen Marktpreises an; sie hat also ihr Minimum bei Ausübungspreisen „am Geld“. Der Name des Begriffes kommt daher, dass die implizite Volatilität als Funktion in Abhängigkeit vom Ausübungspreis einen Kurvenverlauf ergibt, der an einen lächelnden Mund erinnert.
Die Form der Volatilitätskurve ist abhängig vom jeweiligen Markt und vom Optionstyp. In vielen Fällen beobachtet man auch eine Schiefe (englisch skew), bei der die implizite Volatilität bei niedrigen Ausübungspreisen steigt und bei höheren Ausübungspreisen fällt.
Während das Phänomen des Volatilitäts-Smile bei Devisenoptionen schon länger zu beobachten war, trat es für Aktienoptionen erst nach dem Börsencrash von 1987 auf.[1]
Ursachen und Modellierung
Für das Auftreten von Volatilitäts-Smiles gibt es verschiedene konkurrierende Erklärungsansätze, über die keine Einigkeit herrscht. Da das Black-Scholes Modell eine konstante Volatilität voraussetzt, kann es das Auftreten von Volatilitäts-Smiles nicht erklären.
Ein Erklärungsversuch aus der Verhaltensökonomik ist, dass die Marktteilnehmer nach dem Crash von 1987 aus Angst vor einem erneuten Crash Verkaufsoptionen, die weit aus dem Geld sind, bevorzugten, da diese eine günstige Absicherung gegen Kursabstürze darstellen. Dies erklärt eine höhere implizite Volatilität bei niedrigen Ausübungspreisen. Da diese Erklärung suggeriert, dass der Markt Optionen nicht rational bepreist, wird sie von Vertretern der Markteffizienzhypothese abgelehnt.[2]
Andere Erklärungen besagen, dass die Modellannahmen von Black-Scholes zu stark vereinfachend sind. Wenn die Volatilität nicht als konstant angenommen wird, sondern vom aktuellen Preis des Basiswerts sowie von der Zeit abhängt, spricht man von lokaler Volatilität. Wichtige Modelle hierfür sind das zeitdiskrete Derman-Kani-Modell[3] (eine Erweiterung des Binomialmodells) sowie das kontinuierliche Modell von Bruno Dupire[4].
Ein weiterer Ansatz zur Erklärung des Volatilitäts-Smile ist, die Volatilität als veränderliche Größe zu beschreiben. Bekannte Modelle mit veränderlicher Volatilität sind das Heston-Modell und die GARCH-Modelle.
Eine andere Erweiterung besteht darin, den stetigen Wiener-Prozess, der für den Logarithmus des Basiswerts im Black-Scholes-Modell angenommen wird, durch einen Sprünge aufweisenden stochastischen Prozess zu ersetzen. Dies führt zu Sprungdiffusionsmodellen wie dem von Robert Carhart Merton[5], welche ebenfalls zur Modellierung von Volatilitäts-Smiles verwendet werden können.
Eine Modellerweiterung, die die oben erwähnte Volatilitätsschiefe erklären kann, ist die Miteinbeziehung von Ausfallrisiken ins Optionspreismodell.[6]
Literatur
- Jim Gatheral: The volatility surface. A practitioner's guide, Wiley (2006)
- Paul Wilmott: Paul Wilmott on quantitative finance, Wiley, 2nd edition (2006)
- Neil A. Chriss: Black Scholes and beyond. McGraw-Hill Professional (1997)
Einzelnachweise
- Mark Rubinstein: Implied Binomial Trees. Journal of finance, 1994
- Hersh Shefrin: A behavioral approach to asset pricing. Academic Press, 2005.
- Emanuel Derman, Iraj Kani: Riding on a Smile RISK, 7(2), 1994, pdf
- Bruno Dupire: Pricing with a Smile, Risk (1994)
- Robert C. Merton: Option pricing when underlying stock returns are discontinuous. Journal of financial economics, 1976
- Jim Gatheral: The volatility surface. A practitioner's guide, Wiley (2006) Kapitel 6