Urlauberdilemma
Das Urlauberdilemma ist ein 1994 von Kaushik Basu erdachtes, spieltheoretisches Gedankenexperiment, bei dem die Beteiligten durch spieltheoretisch falsches Handeln mehr Gewinn erzielen können als bei der „korrekten“ Lösung. Der englische Originaltitel „traveler's dilemma“ ist nicht mit dem „traveling salesman problem“, also dem Problem des Handlungsreisenden, zu verwechseln. Das Dilemma ist kein Nullsummenspiel, denn es werden immer positive Werte, also Gewinne, bezahlt, auch wenn der Vorteil des einen Spielers dem Nachteil des andern Spielers gleich ist.
Rahmenhandlung
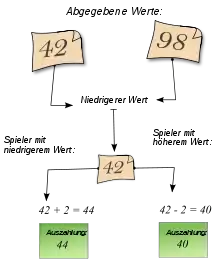
Die Hintergrundgeschichte existiert in mehreren Versionen, da Basu das Dilemma mehrfach publizierte und dabei immer weiter ausschmückte. Die hier dargestellte Fassung stammt aus einem Artikel aus der Zeitschrift „Spektrum der Wissenschaft“, die vermutlich erste deutsche Erklärung des Dilemmas.
Tanja und Markus haben zwar zur gleichen Zeit auf derselben entlegenen Pazifikinsel Urlaub gemacht; aber sie lernen sich erst nach dem Rückflug auf dem heimatlichen Flughafen kennen – im Büro der Schadenersatzabteilung. Die Fluggesellschaft hat nämlich die antiken Vasen zerdeppert, von denen sich jeder der beiden vor Ort ein Exemplar gekauft hatte. Der Sachbearbeiter erkennt ihren Anspruch ohne weiteres an, kann jedoch beim besten Willen den Wert der Kunstwerke nicht beurteilen. Von einer Befragung der Reisenden verspricht er sich, abgesehen von großen Übertreibungen, herzlich wenig. Nach einigen Überlegungen entschließt er sich deshalb für ein trickreicheres Vorgehen. Er bittet beide, unabhängig voneinander den Wert der Vase in Euro auf ein Stück Papier zu schreiben, und zwar als ganze Zahl zwischen 2 und 100. Jegliche vorherige Absprache ist selbstverständlich verboten. Was er aber vorher bekannt gibt, ist das Auszahlungsverfahren: Geben beide denselben Wert an, so wird er diesen als den wahren Kaufpreis erachten und ihn an jeden von ihnen auszahlen. Unterscheiden sich die Angaben jedoch, so wird er die niedrigere Preisangabe für wahr und die höhere für einen Betrugsversuch halten. In diesem Fall bekommen beide den niedrigeren Betrag erstattet – allerdings mit einer Abweichung: Derjenige von beiden, der den niedrigeren Wert aufgeschrieben hat, bekommt 2 Euro mehr als Belohnung für Ehrlichkeit, dem anderen wird eine Strafgebühr von 2 Euro abgezogen. Wählt Tanja also zum Beispiel 46, Markus aber 100, so bekommt sie 48 Euro und er nur 44.[1]
Das Paradoxon
| 2 | 3 | 4 | … | 98 | 99 | 100 | |
|---|---|---|---|---|---|---|---|
| 2 | 2 2 | 4 0 | 4 0 | … | 4 0 | 4 0 | 4 0 |
| 3 | 0 4 | 3 3 | 5 1 | 5 1 | 5 1 | 5 1 | |
| 4 | 0 4 | 1 5 | 4 4 | 6 2 | 6 2 | 6 2 | |
| … | … | … | |||||
| 98 | 0 4 | 1 5 | 2 6 | … | 98 98 | 100 96 | 100 96 |
| 99 | 0 4 | 1 5 | 2 6 | 96 100 | 99 99 | 101 97 | |
| 100 | 0 4 | 1 5 | 2 6 | 96 100 | 97 101 | 100 100 | |
Das Erstaunliche an diesem Spiel ist, dass die Spieltheorie vorhersagt, rationalerweise wäre von den Spielern der Wert 2 € zu wählen. Diese Antwort widerspricht natürlich dem gesunden Menschenverstand, ist aber durch einige logische Überlegungen nachzuvollziehen.
Tanja und Markus – beziehungsweise abstrakt A und B – werden sich überlegen, wie der jeweils Andere handeln wird. Die erste Wahl ist logischerweise 100, da sich so der meiste Gewinn erzielen lässt. Allerdings kann Spieler A seine Auszahlung sogar auf 101 erhöhen, indem er 99 angibt und den Bonus einnimmt. Da Spieler B genauso denkt wie Spieler A – das ist eine der Eigenschaften, die die Spieltheorie unter dem Begriff „rational“ zusammenfasst – wird er zu demselben Schluss gelangt sein, sodass nun beide 99 wählen. A weiß, dass B genauso denkt, und versucht, wieder auf dieselbe Weise, seine Auszahlung zu erhöhen: Er wählt den nächstniedrigeren Wert 98, was ihm den Bonus (B wählt immer noch 99) und damit immerhin noch eine Auszahlung von 100 einbringt. B wird nun wieder nachziehen, durch dieselben Schlüsse von A unterboten werden usw. Die Folge ist, dass es zu jeder Zahl eine bessere gibt, und zwar die jeweils niedrigere. Also ist die logische Wahl für beide Spieler 2. Durch das Abweichen um eine Einheit (also auf 3) kann man nur eine Verschlechterung bewirken, unabhängig davon, was der andere Spieler wählt, ist die Auswahl 2 günstiger. Hier liegt also das sogenannte Nash-Gleichgewicht des Spiels. Die Wahl der Gleichgewichtsstrategie 2 durch beide Spieler ist im Endeffekt allerdings alles andere als vorteilhaft, da so nur minimale Auszahlungen erreicht werden können.[1]
Der Denkfehler
Es sind mindestens 3 mögliche Ziele der handelnden Personen zu unterscheiden. Die Wahl von 2 Euro ist für Spieler A unter der Zielsetzung, möglichst nicht weniger als Spieler B zu gewinnen, richtig und nachvollziehbar. Verfolgt ein Spieler das Ziel, einen möglichst hohen Gesamtauszahlungsbetrag der Versicherung zu erreichen, so wird er 100 Euro wählen. Schwieriger ist die Entscheidung für Spieler A, wenn es ihm um eine persönliche Gewinnmaximierung geht. Lediglich wenn er davon ausgeht, dass Spieler B mit vernachlässigbarer Wahrscheinlichkeit einen höheren Betrag als 3 Euro wählt, wird er selbst 2 Euro wählen. Spieler B wird aber eher selbst eine persönliche Gewinnmaximierung anstreben und einen hohen Betrag nennen.
Richtig ist, dass Spieler A beim Wechsel von 100 auf 99 Euro nicht schlechter abschneiden kann. Hat Spieler B 100 Euro gewählt, so gewinnt Spieler A 101 Euro, wählte Spieler B 99 Euro, so erhält Spieler A auch 99 Euro, jedoch gegenüber 97 Euro bei der ursprünglichen Wahl von 100 Euro. Ein Wechsel von 100 auf 98 Euro ist auch sinnvoll. Ein Wechsel von 99 auf 98 Euro ist es aber nicht in jedem Fall. Unter der Annahme, dass Spieler B Beträge im oberen Bereich mit annähernd gleicher Wahrscheinlichkeit wählt, wäre ein Wechsel von 97 auf 96 Euro mit keinem Vorteil mehr verbunden.
Gemischte Strategien als Erklärungsmöglichkeit
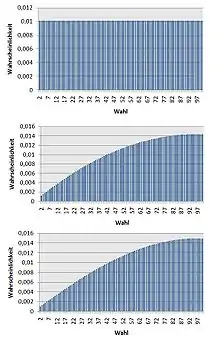
Mitte: Verteilung der Wahrscheinlichkeitswerte für Spieler A, wenn sich Spieler B die obere Verteilung hält und der Erwartungswert zur Wahrscheinlichkeit proportional ist.
Unten: Die Grenzwerte weichen von der Parabelform nur geringfügig ab
Eine Möglichkeit, das menschliche Verhalten anzunähern, beruht auf der Wahrscheinlichkeitstheorie statt auf der Spieltheorie. Die Spieler wählen keinen bestimmten Wert (von 2–100), sondern jeden Wert mit einer bestimmten Wahrscheinlichkeit. Da Spieler A nicht weiß, wie B seine Wahrscheinlichkeiten wählt, kann er beispielsweise eine Gleichverteilung annehmen. Für jede Wahl von A kann man nun seinen Erwartungswert ausrechnen. Wenn man annimmt, die Wahrscheinlichkeit, mit der A einen bestimmten Wert wählt, sei proportional zur Auszahlung, die er im Mittel bei der Wahl dieses Wertes zu erwarten hat, wenn sich B an seine eigene Verteilung hält (dem Erwartungswert), kann man die Verteilung der Wahrscheinlichkeiten von A berechnen. Das Ergebnis kann man nun statt der Gleichverteilung für B einsetzen. Wiederholt man das Verfahren mit der neuen Ausgangsverteilung, entsteht eine abweichende Verteilung, die man wiederum als Startverteilung eingeben kann. Bei mehrmaligem Durchführen konvergiert die Verteilung gegen eine Grenzverteilung mit dem Maximum bei 97.[2]
Wirkliches Verhalten von Menschen im Urlauberdilemma
Im Laufe der Zeit wurden mehrere Versuche durchgeführt, um herauszufinden, wie sich „echte“ Menschen im Urlauberdilemma verhalten. Fast immer gab (bei niedrigen Boni) die überwiegende Mehrheit das Maximum (in der ursprünglichen Version 100) an, der Rest verteilt sich zu ungefähr gleichen Teilen auf die drei Alternativen: Nash-Gleichgewicht, Werte dicht unter dem Maximum und zufällige Werte dazwischen. In jedem Fall lag der Durchschnitt der genannten Werte relativ hoch.
Ein wirklicher Spieler wird das oben berechnete Nash-Gleichgewicht nicht einfach akzeptieren, sondern Teile der logischen Schlusskette infrage stellen. Eventuell wird er die Versicherung als weiteren Gegenspieler betrachten oder die möglichen Gewinne in Bezug zu einem unbeteiligten fiktiven weiteren Mitspieler setzen.
Man muss beachten, dass der Wechsel zurück von 99 auf 100 Euro für einen streng logischen Spieler nur ausgeschlossen ist, wenn er das Spiel als reinen Zweikampf zwischen Tanja und Markus begreift. Durch einen Wechsel zurück hätte der andere Spieler die niedrigere Zahl angegeben und der Wechsler würde den Abzug bekommen. Auch ein Wechseln beider Spieler ist unmöglich, da jeder das Spiel nur aus seiner Perspektive betrachtet. Die ursprüngliche 100 × 100-Tabelle ist sozusagen auf eine 99 × 99-Tabelle verkürzt worden. Durch die Rückwärtsinduktion bleibt unter dieser Voraussetzung am Ende nur eine Zelle mit dem Wert 2 übrig.
Entgegen den theoretischen Überlegungen wird ein Mensch in der beschriebenen Situation das Augenmerk auf die persönliche Gewinnmaximierung richten. Der Vergleich mit dem anderen Versicherungsnehmer bleibt für ihn zweitrangig. Er wird es vorziehen einen möglichst hohen Betrag zu wählen, um damit die Chance auf einen hohen Gewinn zu wahren. Unsinnig wäre aus dieser Sicht einen möglichst kleinen Betrag zu wählen, um lediglich 2 Euro besser als der Gegenspieler abzuschneiden. Dadurch, dass der andere Spieler auch eine entsprechend hohe Zahl wählt, zahlt sich die Handlung erst aus. Basu nennt dies eine „übergeordnete Rationalität“.
Parallelen zu anderen Problemen
Das Urlauberdilemma ist im Grunde eine Verallgemeinerung des bekannteren Gefangenenproblems. Dieses entspricht einem Fall des Urlauberdilemmas mit der Untergrenze 2 und der Obergrenze 3, also den oberen linken vier Zellen der Auszahlungsmatrix. Das Gefangenendilemma wirft daher ähnliche Schwierigkeiten auf wie das Urlauberdilemma; der Unterschied zwischen der menschlichen Wahl und der Vorhersage der Spieltheorie tritt allerdings beim Urlauberdilemma wesentlich stärker zu Tage.
Siehe auch
Einzelnachweise
- Kaushik Basu: Das Urlauberdilemma. In: Spektrum der Wissenschaft. 08/07, 2007, S. 82–88.
- Christoph Pöppe: Was ist wirklich rational?. In: Spektrum der Wissenschaft. 10/07, 2007, S. 98–103.