Uran-Blei-Datierung

Die Uran-Blei-Datierung ist eine absolute Datierungsmethode, bei der die radioaktiven Zerfallsreihen von Uran ausgenutzt werden, um Proben zu datieren. Mit dieser Methode werden z. B. irdisches Gestein oder auch Meteoriten datiert. Das heute angenommene Alter der Erde von 4,55 Milliarden Jahren wurde zuerst von Fritz Houtermans[1] und Clair Cameron Patterson[2][3] mit der Uran-Blei-Datierung bestimmt. Das Alter des Sonnensystems wurde mittels dieser Datierungsmethode, angewandt auf die vermutlich ältesten in unserem Sonnensystem entstandenen Mineralien, den Calcium-Aluminium-reichen Einschlüssen in Meteoriten, auf 4,567 Milliarden Jahre bestimmt.[4] Für die ältesten auf der Erde entstandenen Minerale, Zirkone, die in Gesteinen in Australien gefunden wurden, ermittelte man ein Alter von bis zu 4,404 Milliarden Jahren.[5]

Grundlagen

Es gibt zwei Zerfallsreihen, die jeweils bei Uran-Isotopen beginnen und über mehrere Zwischenschritte bei Blei-Isotopen enden:

Uran-Radium-Reihe: Uran ²³⁸U → … → Blei ²⁰⁶Pb (Halbwertszeit: 4,5 Milliarden Jahre)
Uran-Actinium-Reihe: Uran ²³⁵U → … → Blei ²⁰⁷Pb (Halbwertszeit: 704 Millionen Jahre)

Die verschiedenen instabilen Zerfallsprodukte in diesen Reihen sind viel kurzlebiger als das jeweilige Uran-Isotop am Anfang der Reihe. Für die Altersbestimmung spielen daher nur die Halbwertszeiten der Uran-Isotope eine wesentliche Rolle. Nach dem Zerfallsgesetz gilt:

{}^{206}\mathrm {Pb} ={}^{238}\mathrm {U} \cdot (1-e^{-\lambda _{238}t}),\quad {\lambda }_{238}=1{,}55125\cdot 10^{-10}\,{\frac {1}{\mathrm {Jahr} }}

{}^{207}\mathrm {Pb} ={}^{235}\mathrm {U} \cdot (1-e^{-\lambda _{235}t}),\quad {\lambda }_{235}=9{,}8485\cdot 10^{-10}\,{\frac {1}{\mathrm {Jahr} }}

Damit lässt sich aus der Messung der Blei-Isotopenverhältnisse und des Pb/U-Verhältnisses das Alter auf drei verschiedene Weisen berechnen. Die ersten zwei Methoden ergeben sich direkt aus der Umformung des jeweiligen Zerfallsgesetzes:

t={\frac {1}{\lambda _{238}}}\cdot \ln \left(1+{\frac {{}^{206}\mathrm {Pb} }{{}^{238}\mathrm {U} }}\right)

t={\frac {1}{\lambda _{235}}}\cdot \ln \left(1+{\frac {{}^{207}\mathrm {Pb} }{{}^{235}\mathrm {U} }}\right)

Aus beiden Zerfallsgesetzen zusammen lässt sich auch einfach die dritte Gleichung für das Alter ableiten, in der keine Verhältnisse von Isotopen verschiedener Elemente, sondern nur noch Verhältnisse von Isotopen jeweils eines Elementes vorkommen:

{\frac {{}^{207}\mathrm {Pb} }{{}^{206}\mathrm {Pb} }}={\frac {{}^{235}\mathrm {U} }{{}^{238}\mathrm {U} }}\cdot {\frac {(e^{\lambda _{235}t}-1)}{(e^{\lambda _{238}t}-1)}}

Aus dieser Gleichung lässt sich durch iterative numerische oder grafische Verfahren das Alter $t$ bestimmen. Prinzipiell muss dafür nur das Verhältnis der Blei-Isotope ²⁰⁷Pb : ²⁰⁶Pb gemessen werden, wenn man davon ausgeht, dass das heutige natürliche Uran-Isotopenverhältnis auf der Erde homogen ist. Dies nahm man lange an, der Wert sollte bei ²³⁵U : ²³⁸U = 1 : 137,88 liegen.[6] Neue Messungen beziffern ihn jedoch auf ²³⁵U : ²³⁸U = 1 : 137,818 ± 0,045 (2σ), er kann zudem je nach Fundort leicht verschieden sein.[7] Da Isotopenverhältnisse eines Elementes viel genauer bestimmt werden können als das Verhältnis von verschiedenen Elementen, ist diese Methode sehr genau. Voraussetzung dieser Methode ist, dass das heutige Uran-Isotopenverhältnis in der Probe bekannt ist. Insbesondere die Anwendung zur Meteoriten-Datierung setzt eine Homogenität der Uran-Isotope im solaren Urnebel voraus, solange man das terrestrische Uran-Isotopenverhältnis zur Berechnung des Alters benutzt. Allerdings kann das benötigte Uran-Isotopenverhältnis im Prinzip auch in jeder individuellen Probe mitbestimmt werden, so dass diese Annahme nicht zwingend nötig ist bzw. sogar direkt überprüft werden kann. Eine aussagekräftige Methode, um zu überprüfen, ob die jeweiligen notwendigen Voraussetzungen bei einer konkreten Probe gegeben sind, ist die Anwendung des Konkordia-Diagrammes.

Ein weiterer Vorteil dieser Methode ist, dass die Zerfallskonstanten von Uran mit einer Genauigkeit im Promillebereich bekannt sind, während die Zerfallskonstanten anderer zur Datierung verwendeter radioaktiver Elemente in der Regel nur mit einer Genauigkeit im Prozentbereich bekannt sind.

Konkordia-Diagramm

Das Konkordia-Diagramm stellt eine Möglichkeit dar, die Zuverlässigkeit der gemessenen U-Pb-Alter nachzuprüfen. Trägt man das gemessene ²⁰⁶Pb/²³⁸U-Verhältnis und das ²⁰⁷Pb/²³⁵U Verhältnis einer gemessenen Probe in das Konkordia-Diagramm ein, so sollte der Datenpunkt im Idealfall auf der Konkordia genannten Kurve liegen. Das ist etwa bei Kristallen der Fall, die nur eine einstufige Geschichte hinter sich haben, also nach ihrer Kristallisation keine Störung im Uran-Blei-Isotopensystem mehr erfahren haben. Liegen die gemessenen Isotopenverhältnisse auf der Konkordia, ist also eine einstufige Geschichte anzunehmen und das Alter kann als sehr zuverlässig angesehen werden.

Eine Störung des U-Pb-Isotopensystems durch ein späteres als das zu datierende Ereignis kann z. B. eine Metamorphose des Gesteins oder auch Bleiverlust infolge von Diffusion sein. Ist die Probe gestört worden, so liegt der Datenpunkt daneben d. h., er ist diskordant. Auch nichtradiogene Bleianteile, d. h. Blei aus anderen Quellen als dem Zerfall von Uran (z. B. primordiales Blei), können eine Abweichung von der Konkordia verursachen, falls sie bei den Blei-Isotopenmessungen nicht hinreichend korrigiert wurden. Tatsächlich haben viele Gesteine eine komplexe Geschichte hinter sich, weswegen sich eine große Anzahl der in der Praxis gemessenen Uran-Blei-Verhältnisse als diskordant erweist.

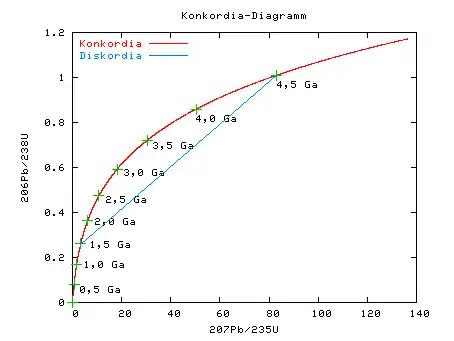
Konkordia-Diagramm

Selbst bei diskordanten Uran-Blei-Messungen kann aber häufig die Geschichte eines Gesteins rekonstruiert werden. Das ist der Fall, wenn Kristalle eines Gesteins etwa nach der ursprünglichen Kristallisation durch ein weiteres singuläres Ereignis, z. B. eine Metamorphose, gestört worden sind, also insgesamt eine zweistufige Geschichte aufweisen. Dann liegen die Datenpunkte solcher Kristalle im Konkordia-Diagramm auf einer Geraden, welche die Konkordia zu den Zeitpunkten des ersten Ereignisses (Kristallisation) und des zweiten Ereignisses (Metamorphose) schneidet. Eine solche Gerade wird Diskordia genannt. Misst man also mehrere Kristalle aus einem Gestein, welche alle dieselbe zweistufige Geschichte hinter sich haben, kann die Diskordia an die Datenpunkte angepasst werden, und damit die Schnittpunkte mit der Konkordia und deren zugehörige Zeitpunkte bestimmt werden.

Ein mögliches Problem kann hier sein, dass, wenn das Uran-Blei-Isotopensystem durch kontinuierlichen Bleiverlust gestört wurde, die Datenpunkte ebenfalls in einem weiten Bereich angenähert auf einer Geraden liegen können und erst bei kleinen ²⁰⁷Pb/²³⁵U-Verhältnissen zum Ursprung des Diagramms hin abbiegen. Die Gefahr ist hier, dass eine an solche Daten angepasste Gerade fälschlich als Diskordia interpretiert werden kann.

Korrektur des nichtradiogenen (primordialen) Blei-Anteils

Neben einem diskordanten Datenpunkt im Konkordia-Diagramm, welcher durch nichtradiogenes (auch primordial genanntes) Blei verursacht werden kann, ist auch das Bleiisotop ²⁰⁴Pb ein wichtiger Indikator für das Vorhandensein von nichtradiogenem Blei in einer Probe. Es gibt nämlich keine natürliche Zerfallsreihe in das Isotop ²⁰⁴Pb und also auch kein radiogenes ²⁰⁴Pb, sondern dieses Bleiisotop ist vollständig primordial und die Häufigkeit deswegen ein direktes Maß für den Anteil des nichtradiogenen Bleis in der Probe.

Bei Proben oder Mineralseparationen, in denen nichtradiogenes Blei einen nicht zu vernachlässigenden Anteil darstellt, muss dieses vor der Altersberechnung korrigiert werden. Dies geschieht meist, indem mit der gemessenen ²⁰⁴Pb Häufigkeit und den bekannten Isotopen-Verhältnissen des primordialen Bleis die primordialen ²⁰⁶Pb- und ²⁰⁷Pb-Häufigkeiten bestimmt werden und von den entsprechenden gemessenen Häufigkeiten dieser Isotope subtrahiert werden. Als Resultat erhält man die radiogenen ²⁰⁶Pb- und ²⁰⁷Pb-Häufigkeiten, mit denen dann die Alter berechnet werden können.

Wichtig bei dieser Korrektur ist die Kenntnis der Isotopen-Verhältnisse des primordialen Bleis. Diese wurden beispielsweise durch Tatsumoto et al. bestimmt und 1973 publiziert[8] und später durch Göpel et al. (1985) bestätigt. Die Untersuchungen von Göpel et al. unterstützen auch stark die Annahme, dass das primordiale Blei in der Protoplanetaren Scheibe homogen war.[9]

Entwicklung der Uran-Blei-Datierung

Eine Datierung aufgrund radioaktiven Zerfalls von Uran schlug zuerst 1905 Ernest Rutherford vor. Nachdem Bertram B. Boltwood 1907 Blei als das Endprodukt des Uranzerfalls nachgewiesen hatte, wurden 1911 von Arthur Holmes Alter von bis zu 1,64 Milliarden Jahren für einige Gesteine angegeben. Diese Alter waren aber zu hoch, da sie nicht auf Isotopen-Verhältnissen basierten, sondern auf den chemischen Verhältnissen von Uran und Blei. Isotope waren damals noch unbekannt.

Isotopenverhältnisse von Blei wurden erst 1927 durch Francis William Aston gemessen. Im Jahre 1930 bestimmte Otto Hahn das Alter der Erde mit der Uran-Blei-Methode auf 1,5 bis 3 Milliarden Jahre, wobei er allerdings immer noch chemische Verhältnisse anstatt Isotopen-Verhältnisse zur Berechnung benutzte und die Annahme machte, dass kein primordiales Blei in den von ihm betrachteten Gesteinen vorhanden sei.[10] Ab 1937 unternahm Alfred Nier Messungen von Bleiisotopenverhältnissen mit Massenspektrometern. Dabei versuchte er auch die Isotopenverhältnisse von primordialem Blei zu bestimmen. Die Entwicklung der Atombombe, besonders im Rahmen des Manhattan-Projekts, führte auch zur Entwicklung von verbesserten Techniken zur Bestimmung von Isotopenverhältnissen und zu besserem Verständnis des Uranzerfalls, was die Entwicklung der Uran-Blei-Datierungstechnik stark beschleunigte. 1953 publizierte Clair Cameron Patterson basierend auf Bleiisotopen-Messungen in einem Meteoriten das bis heute akzeptierte Alter der Erde von 4,55 Milliarden Jahren.

Siehe auch

Literatur

J. M. Mattinson (2013): Revolution and evolution: 100 years of U-Pb geochronology. Elements 9, 53–57
B. Heuel-Fabianek (2017): Natürliche Radioisotope: die “Atomuhr” für die Bestimmung des absoluten Alters von Gesteinen und archäologischen Funden. StrahlenschutzPraxis, 1/2017, S. 31–42.

Einzelnachweise

Determination of the Age of the Earth from the Isotopic Composition of Meteoritic Lead. In: Nuovo Cimento. 10, 1953, S. 1623–1633, doi:10.1007/BF02781658
Patterson C., Tilton G. and Inghram M. (1955): Age of the Earth, Science 121, 69–75, doi:10.1126/science.121.3134.69.
Patterson C. (1956): Age of meteorites and the Earth, Geochimica et Cosmochimica Acta 10, 230–237
Amelin Y., Krot A. N., Hutcheon E. D., and Ulyanov A. A. (2002): Lead isotopic ages of chondrules and calcium-aluminum-rich inclusions, Science, 297, 1678–1683, doi:10.1126/science.1073950.
S. A. Wilde, J. W. Valley, W. H. Peck, C. M. Graham (2001): Evidence from detrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyr ago, Nature, 409, 175–178. (PDF-Datei; 197 kB)
Steiger and Jäger: Submission on geochronology: Convention on the use of decay constants in geo- and cosmochronology, Earth and Planetary Science Letters, 36, 1977, 359–362
Hiess et al.: 238U/235U Systematics in Terrestrial Uranium-Bearing Minerals, Science, 335, 2012, 1610–1614, doi:10.1126/science.1215507
Tatsumoto et al., Science, 180, 1973, 1278–1283
Göpel et al.: U-Pb systematics in iron meteorites – Uniformity of primordial lead, Geochimica et Cosmochimica Acta, 49, 1985, 1681–1695
Otto Hahn: Das Alter der Erde. Die Naturwissenschaften 18 (1930) Heft 47–49, S. 1013–1019

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Determination of the Age of the Earth from the Isotopic Composition of Meteoritic Lead. In: Nuovo Cimento. 10, 1953, S. 1623–1633, doi:10.1007/BF02781658

[2] Patterson C., Tilton G. and Inghram M. (1955): Age of the Earth, Science 121, 69–75, doi:10.1126/science.121.3134.69.

[3] Patterson C. (1956): Age of meteorites and the Earth, Geochimica et Cosmochimica Acta 10, 230–237

[4] Amelin Y., Krot A. N., Hutcheon E. D., and Ulyanov A. A. (2002): Lead isotopic ages of chondrules and calcium-aluminum-rich inclusions, Science, 297, 1678–1683, doi:10.1126/science.1073950.

[5] S. A. Wilde, J. W. Valley, W. H. Peck, C. M. Graham (2001): Evidence from detrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyr ago, Nature, 409, 175–178. (PDF-Datei; 197 kB)

[6] Steiger and Jäger: Submission on geochronology: Convention on the use of decay constants in geo- and cosmochronology, Earth and Planetary Science Letters, 36, 1977, 359–362

[7] Hiess et al.: 238U/235U Systematics in Terrestrial Uranium-Bearing Minerals, Science, 335, 2012, 1610–1614, doi:10.1126/science.1215507

[8] Tatsumoto et al., Science, 180, 1973, 1278–1283

[9] Göpel et al.: U-Pb systematics in iron meteorites – Uniformity of primordial lead, Geochimica et Cosmochimica Acta, 49, 1985, 1681–1695

[10] Otto Hahn: Das Alter der Erde. Die Naturwissenschaften 18 (1930) Heft 47–49, S. 1013–1019