Tubulare Umgebung

In d​er Mathematik i​st die tubulare Umgebung o​der Tubenumgebung e​in häufig verwendetes technisches Hilfsmittel d​er Differentialtopologie.

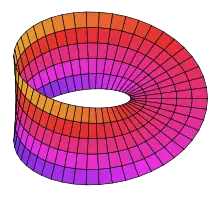
Tubenumgebung einer Kurve in der Ebene

Tubenumgebung einer Kurve in einer nicht-orientierbaren Fläche

Satz von der Tubularen Umgebung

Es sei ${\displaystyle M}$ eine differenzierbare Mannigfaltigkeit und ${\displaystyle N\subset M}$ eine kompakte differenzierbare Untermannigfaltigkeit. Dann gibt es eine Umgebung ${\displaystyle U(N)}$ von ${\displaystyle N}$ in ${\displaystyle M}$ mit der folgenden Eigenschaft:

Es gibt ein Faserbündel ${\displaystyle U(N)\to N}$ mit Totalraum ${\displaystyle U(N)}$, Basis ${\displaystyle N}$ und Faser diffeomorph zu

${\displaystyle B^{k}=\{x\in \mathbb {R} ^{k}\ |\ |x|<1\},k=\dim(M)-\dim(N)}$.

Weiterhin ist ${\displaystyle N\subset U(N)}$ der Nullschnitt dieses Faserbündels.

Diese Umgebung ${\displaystyle U(N)}$ wird als Tubenumgebung von ${\displaystyle N}$ bezeichnet, sie ist nur bis auf Isotopie eindeutig bestimmt.

Siehe auch

• Kragenumgebung

Literatur

• James R. Munkres: Elementary differential topology. Lectures given at Massachusetts Institute of Technology, Fall 1961. Revised edition. In: Annals of Mathematics Studies, No. 54. Princeton University Press, Princeton NJ 1966

Weblinks

• Schnürer: Differentialtopologie (PDF; 755 kB) Satz 1.16