Tibetische astronomische Kalenderrechnung
Die Tibetische astronomische Kalenderrechnung (tib.: lnga bsdus oder yan lag lnga bsdus) ist ein Teilgebiet der Tibetischen Astronomie (tib.: skar rtsis). Ziel dieser astronomischen Zeitrechnung ist der Aufbau des tibetischen Kalenders als Hilfsmittel der Zeitordnung und der Orientierung in der Zeit.

Für die tibetische Zeitrechnung ordnet sich das Weltgeschehen zeitlich durch Zeitzyklen, also durch periodisch wiederkehrende Zeiteinheiten wie „Weltalter“, „Sechzig-Jahres-Zyklus“, Jahr, Monat und Tag. Dabei sind die Zeiteinheiten dieser Zyklen in der Regel durch astronomische Phänomene definiert:
Das Weltalter beginnt und endet mit dem Zusammentreffen aller Planeten am Nullpunkt der Ekliptik, das Jahr ergibt sich aus der Vollendung der scheinbaren Umdrehung der Sonne um die Erde, der Monat beschreibt die Zeitspanne zwischen zwei Neumonden und der Kalendertag ist der natürliche Tag.
Im Rahmen der Zeitrechnung behandelt die tibetische Astronomie unter anderem die scheinbare Bewegung der Sonne und die Berechnung der ekliptikalen Länge des Mondes.
Durchgeführt wurden die astronomischen Berechnungen mit dem tibetischen Sandabakus.
Die Tibetische Kalenderrechnung wird auch heute noch sowohl in Tibet als auch außerhalb Tibets zur Erstellung des jährlichen Kalenders praktiziert.
Geschichtlich gesehen gründet die Tibetische Kalenderrechnung auf den Lehren des 1. Kapitels des Kālacakratantra und ist somit indischer Herkunft.
Zyklische Zeiteinheiten
Weltzeitalter
Den größten Zeitzyklus bilden die vier Weltzeitalter (tib.: dus bzhi). Die Länge eines Weltzeitalters wird als der Zeitabschnitt zwischen zwei aufeinanderfolgenden Konjunktionen aller in Tibet bekannten, beweglichen Himmelskörper bzw. Planeten am Nullpunkt der Ekliptik definiert. Außerdem ist dieses Ereignis stets dadurch gekennzeichnet, dass das astronomische Kalenderjahr beginnt und ein bestimmter, sechzig Jahre umfassender Jahreszyklus anfängt. Im Tibetischen wird dieses Ereignis einer großen Konjunktion als stong 'jug „Eintritt ins Leere“ bezeichnet.
Das Kālacakratantra nennt vier Weltalter, die unterschiedlicher Länge haben, die diese astronomischen Bedingungen erfüllen sollen und die aufeinander gefolgt sind, nämlich das
- Sanskrit: kṛtyuga, tib.: rdzogs ldan gyi dus mit 1.728.000 Jahren, das
- Sanskrit: tretāyuga, tib.: gsum ldan gyi dus .mit 1.269.000 Jahren, das
- Sanskrit: dvāparayuga, tib.: gnyis ldan gyu dus mit 864.000 Jahren und das
- Sanskrit: kaliyuga, tib.: rtsod pa'i dus mit 432.000 Jahren.
Die tibetischen Astronomen des 15. Jahrhunderts fanden nun heraus, dass mit dem im Kālacakratantra vorliegenden Zahlenmaterial von chronologischen Größen und Anfangswerten der Planeten eine große Konjunktion weder in diesen genannten Zeitintervallen noch überhaupt möglich war.
So verwendet das Kālacakratantra als Epoche seiner Zeitrechnung den Beginn des Monats nag zla ba (Sanskrit: Caitra) des Jahres 806, welches dem 23.3.806 entspricht. Am Beginn dieses Tages stehen nach dem Kālacakratantra Sonne und Mond am Nullpunkt der Ekliptik, welcher mit dem Beginn des Tierkreiszeichens Widder (tib.: lug) bzw. des Mondhauses tha skar zusammenfällt. Das Jahr 806 ist das 20. Jahr des Sechzig-Jahres-Zyklus, der in dem Jahr 787 beginnt.
Da eine große Konjunktion mit dem Beginn am 1. Jahres eines Sechzig-Jahres-Zyklus stattfinden muss und da das Umrechnungsverhältnis von solaren Monat zu synodischem Monat generell mit
angegeben wird, bedeutet dies nach den nachprüfbaren Berechnungen der tibetischen Astronomen, dass zu Beginn eines 20. Jahres eines Sechzig-Jahres-Zyklus der Beginn eines synodischen Monats niemals mit dem Beginn eines solaren Monats zusammenfallen kann.
Umgekehrt gerechnet ergab dies, dass bei Akzeptanz der entsprechenden Werte des Kālacakratantra eine große Konjunktion zu Anfang eines Sechzig-Jahres-Zyklus nicht erfolgen konnte.
Mit dieser und weiterer Kritik an den Anfangswerten errechneten die Astronomen der Phugpa-Schule für die Periode der Eintreffens großer Konjunktionen einen Wert, der im Weißen Beryll des Regenten Sanggye Gyatsho mit 279 623 511 548 502 090 600 Jahren beziffert wurde. Dies sind in Zahlennamen ausgedrückt 279 Trillionen, 623 Billiarden, 511 Billionen, 548 Milliarden, 502 Millionen, 90 Tausend und 6 Hundert Jahre.
Der Zyklus von 60 Jahren
Die nächste kleinere zyklische Zeiteinheit ist ein Zeitraum von 60 Jahren. In der Astronomie ist mit dem Sechzig-Jahres-Zyklus immer der sogenannte Rab byung-Zyklus indischer Herkunft gemeint. Die Zyklen werden mit Ordinalzahlen gezählt. Die einzelnen Jahre tragen individuelle Bezeichnungen.
Das Jahr
Die folgende kleinere zyklische Zeiteinheit wird als Jahr (tib.: lo) bezeichnet. Es ist einerseits festgelegt als die Zeit, die die Sonne benötigt, um die 12 Tierkreiszeichen zu durchlaufen. Dies ist das Tropische Jahr bzw. Solar-Jahr. Anderseits existiert als weitere Zeiteinheit das tibetische Kalenderjahr mit zeitlich unterschiedlichen Längen von jeweils 12 oder 13 synodischen Monaten. Die Größe des Solar-Jahres diente aber als Richtschnur dazu, die unterschiedlichen Jahreslängen des Kalenders zu regulieren.
Monate
Die nächste kleinere zyklische Zeiteinheit ist der Monat (tib.: zla ba). Hierzu unterscheiden die Astronomen drei Arten von Monaten:
- Solar-Monat (tib.: khyim zla), d. i. die Zeitspanne, die die mittlere Sonne benötigt, um ein Tierkreiszeichen zu durchlaufen.
- Lunarer Monat (tib.: tshes zla), d. i. die Zeitspanne, die der Mond für eine Änderung der Elongation von 360 Grad benötigt.
- Kalendermonat (tib.: zla ba), d i. eine Zeitspanne von 29 oder 30 natürlichen Tagen. Sie beginnt einen Tag nach dem natürlichen Tag, in dem der vorherige Lunare Monat endet. Sie wird mit dem natürlichen Tag beendet, in dem der laufende Lunare Monat endet.
Tage
Es gibt in der tibetischen Astronomie drei Arten von Tagen (tib.: zhag gsum):
- Zodiak-Tag (tib.: khyim zhag), d. i. eines Solar-Monats. Der Zodiak-Tag ist eine, nur für astronomische Berechnungen gebrauchte, nicht erfahrbare Zeitgröße.
- Lunarer Tag (tib.: tshes zhag), d. i. die Zeitspanne, die der Mond für eine Elongation (Winkelabstand von Sonne und Mond) von 12 Grad benötigt. Ein lunarer Monat umfasst 30 lunare Tage. Der Lunare Tag ist ebenfalls eine faktisch nicht erfahrbare, astronomische Zeitgröße. Er hat aber insofern für die Zeitordnung eine besondere Bedeutung, als er die Zählgrößen für die Nummerierung der natürlichen Tage innerhalb eines Monats liefert. Da bei der Berechnung der zeitlichen Länge eines lunaren Tages die Unregelmäßigkeit der Bewegung von Sonne und Mond durch sogenannte Mittelpunktsgleichungen berücksichtigt wird, bildet die Berechnung der lunaren Tage einen der schwierigsten Teile der tibetischen Kalenderrechnung.
- Natürlicher Tag (tib.: nyin zhag), die Zeitspanne zwischen zwei aufeinanderfolgenden Morgendämmerungen. Die Zeiteinheit natürlicher Tag wird in der modernen Wissenschaft meist mit dem Symbol „d“ bezeichnet.
Astronomische Unterteilung der drei Tagesarten
Für astronomische Berechnungen werden alle drei Tagesarten wie folgt unterteilt:
- 1 Tag = 60 chu tshod,
- 1 chu tshod = 60 chu srang,
- 1 chu srang = 6 dbugs.
Es ist zu beachten, dass die absolute Größe dieser Zeitgrößen je nach Tagesart unterschiedlich ist.
Durchführung der Kalenderrechnung
Zielsetzung

Im Zentrum steht die Berechnung des Datums (lunarer Tag) innerhalb eines Monats, mit dem ein natürlicher Tag bzw. Wochentag innerhalb eines Monats gezählt wird. Des Weiteren werden für jeden Wochentag die ekliptikalen Längen von Sonne und Mond sowie zwei weitere astrologisch bedeutsame Größen berechnet, die als byed pa (Sanskrit: karaṇa) und sbyor ba (Sanskrit: yoga) bezeichnet werden. Da die Rechnungen auf die Feststellung dieser fünf Komponenten hinauslaufen, wird die Kalenderrechnung auch als yan lag lnga bsdus „Zusammenfassung von fünf Komponenten“, häufig abgekürzt zu lnga bsdus, bezeichnet.
Mathematische Verfahrensweise
Tibetische Kalenderrechnungen sind Programmtexte, also eine Aneinanderreihung von Rechenvorschriften, zum Aufbau einer Zeitordnung. Die Rechnungen selbst werden auf dem Sandabakus durchgeführt.
Für die im Folgenden verwendete besondere Schreibweise mehrstelliger Zahlen des Sexagesimalsystems vgl. Rechnen mit Zahlen im Sexagesimalsystem. Als besondere Schreibweise wird mit das Ergebnis der Division zweier Ganzer Zahlen ohne Rest und mit der Rest dieser Division bezeichnet.
Strukturen der Zeiteinteilung
Grundsätzlich ist die Basis des Tibetischen Kalenders die Abfolge der natürlichen Tage (tib.: nyin zhag). Die Unterteilung des natürlichen Tages in 21.600 dbugs, das sind hier Atemzüge von der Länge von 4 Sekunden, bildet eine physikalische Grundlage für die Maßgröße dieser Zeiteinheit.
Eine Unterscheidbarkeit der natürlichen Tage entsteht durch ihre Bezeichnung als Wochentage. Die sieben Wochentage tragen in zyklischer Abfolge die Bezeichnungen der sieben wichtigsten Planeten. Sie werden in den astronomischen Berechnungen von 0 bis 6 gezählt. Dabei ist der mit 0 gezählte Wochentag immer der Samstag (tib.: spen pa). Die Woche selbst wird auch als Zyklus oder Rad der Planeten (tib.: gza' 'khor) bezeichnet. Das Rad der Wochentage oder Planeten verläuft kontinuierlich und in die Vergangenheit und Zukunft ohne Ende.
Der Monat als das nächste größere Zeitsegment zur Einordnung der natürlichen Tage definiert sich letztendlich aus der Zeitspanne zwischen zwei Neumonden, was ebenfalls eine gut erfahrbare Zeitgröße ist. Grundsätzlich ist es aber so, dass die zeitlichen Längen synodischer Monate zwischen 29,272 d und 29,833 d variieren. Dies hat zur Folge, dass eine ganze Zahl natürlicher Tage nicht in den Zyklus der lunaren Monate passen. Es sind also Anpassungen vorzunehmen, damit die beiden Zyklen ineinanderpassen. Letztendlich läuft dies darauf hinaus, dass die Anzahl der natürlichen Tage eines Monats unterschiedlich groß ist.
Die Einordnung der natürlichen Tage in den Monatszyklus erfolgt nicht durch einfaches Abzählen mit natürlichen Zahlen. Die einzelnen natürlichen Tage werden vielmehr mit der Nummer des lunaren Tages gezählt, der in dem betreffenden natürlichen Tag endet.
Dies hat wegen der unterschiedlichen Länge der lunaren Tage zur Folge, dass in bestimmten Tagen zwei lunare Tage enden können. In diesem Fall wird die Nummer des zweiten lunaren Tages nicht vergeben. Z. B. folgt dann auf den Wochentag Montag mit der Datumszahl neun ein Dienstag mit der Datumszahl 11. Das somit nicht auftretende Datum 10 wird als chad „ausgelassenes Datum“ bezeichnet.
Des Weiteren kann es vorkommen, dass in einem bestimmten Wochentag kein lunarer Tag endet. In diesem Fall wird diesem Wochentag das Datum des folgenden Wochentages zugeordnet. Als Beispiel folgt in diesem Fall auf einen Mittwoch mit der Datumszahl 12 ein Donnerstag mit dem Datum 13 und ein Freitag mit der gleichen Datumszahl 13. Der erste dieser beiden mit gleicher Datumszahl versehenen Tage wird als lhag „zusätzlich“ bezeichnet.
Bei der Einordnung der lunaren Monate, in der Regel sind dies 12, in den Zyklus der tropischen Jahre entstehen vergleichbare Anpassungsprobleme wie bei der Einfügung der natürlichen Tage in den Monatszyklus. 12 Lunare Monate sind kürzer als ein tropisches Jahr. Der Ausgleich erfolgt durch die Einfügung sogenannter Schaltmonate (tib.: zla lhag oder zla bshol).
Epoche und Anfangswerte
Eine Zeitrechnung bedarf eines bestimmten Ausgangspunkts, von dem ausgehend die zeitlichen Strukturen aufgebaut werden. Dieser Zeitpunkt wird allgemein als Epoche bezeichnet. In der astronomischen Zeitrechnung ist dies in der Regel der Beginn des ersten lunaren Tages des ersten astronomischen Monats (nag zla) des ersten Jahres (rab byung genannt) eines der Sechzig-Jahres-Zyklen. Eine der wenigen Ausnahmen ist das Kālacakratantra, dessen Epoche in das Jahr 806 fällt, welches als 20. Jahr eines Sechzig-Jahres-Zyklus gezählt wird. Für den tibetischen Kalender selbst sind Epochen auf den Beginn des ersten natürlichen Tages des ersten zivilen Monats eines Jahres festzulegen.
Das Problem dieser Epochen liegt darin, dass zu diesen Zeitpunkten die Anfänge der verschiedenen Zeitzyklen zumeist gegeneinander verschoben sind. Zwar beginnt das astronomische Jahr immer mit dem 1. lunaren Tag, doch entspricht dieser dann meist nicht dem Anfang des 1. Wochentages, der mit 0 gezählt wird, nämlich des Samstags. Der Jahresanfang korrespondiert meist nicht mit dem Anfang des Solar-Jahres. Die ekliptikalen Längen von Sonne, Mond und der übrigen Planeten sind natürlich nicht gleich Null. Die ideale Epoche wäre somit der Zeitpunkt einer großen Konjunktion, doch ist das Rechnen mit so großen Zahlen auf dem Sandabakus völlig unpraktisch.
In der Kalenderrechnung und Astronomie berücksichtigt man dies durch Anfangswerte (tib.: rtsis 'phro). Im Hinblick auf den Wochentag erfasst dann solch ein Anfangswert den Wochentag und die Tageszeit, an dem der erste lunare Tag beginnt. In Bezug auf Sonne und Mond erfassen die Anfangswerte die ekliptikalen Längen beider Himmelskörper am Beginn des Jahres.
Berechnung der 5 Komponenten eines Tages
Die genaue Aufgabenstellung lautet: In welchem Wochentag W und zu welcher Tageszeit endet der Lunare Tag T des tibetischen lunaren Monats M in einem tibetischen Jahr, das als Jahr J seit Epoche gezählt wird? Wie groß sind die ekliptikalen Längen von Sonne und Mond? Wie errechnen sich die beiden astrologischen Komponenten?
Im Folgenden wird als Epoche die des Kalacakratantra, also der Beginn des tibetischen Jahres gewählt, der in das Jahr 806 fällt.
Hier ist zu beachten, dass tibetische Datumsangaben das Jahr mit der Nummer des Rab byung-Zyklus (Z) und einer Jahresbezeichnung aufführen. Insofern ist individuell abzuzählen, um welches Jahr (JZ) es sich zahlenmäßig sich handelt. Um dann J für die Epoche des Jahres 826 zu ermitteln, rechnet man
- J = (Z -1) · 60 + (JZ – 1) + 221, da das 1. Jahr des 1. Rab byung-Zyklus in das Jahr 1027 fällt.
Beispiele:
- Es handelt sich um das 5. Jahr im 8. Rab byung-Zyklus. Dann ist J = (8-1) · 60 + (5-1)+ 221 = 645
- Es handelt sich um das 58. Jahr im 16. Rab byung-Zyklus. Dann ist J = (16-1) · 60 + (58-1)+ 221 = 1178
In der tibetischen Kalenderrechnung beginnt man naturgemäß mit dem 1. Tag des 1. Monats des neuen Jahres und rechnet für alle Tage des Jahres die fünf Komponenten nacheinander aus. Im Ergebnis erhält man einen Kalender, in dem für alle Tage der 12 bzw. 13 Monate eines Jahres die notwendigen Angaben verzeichnet sind.
Zahl der vergangenen lunaren Monate (tshes zla rnam par dag pa bzw. zla dag)
Ausgangspunkt aller Rechnungen ist zunächst die Ermittlung der Zahl der seit Epoche vergangenen Solar-Monate (tib.: khyim zla). Hierzu multipliziert man die Zahl der „vergangenen Jahre“ ( J-1) mit 12 und addiert die Zahl der „vergangenen Monate“ (M-1) des vorliegenden Jahres:
- SOL(J,M) = (J-1) · 12 + M-1.
Mit dem Kālacakratantra wurde als Größenverhältnis zwischen Solar-Monat und lunarem Monat der Wert.
überliefert. Dieser Umrechnungsfaktor wurde in Tibet niemals in Frage gestellt.
Für die Errechnung der Zahl der vergangenen lunaren Monate (tib.: tshes zla) ist zu beachten, dass bei einer beliebig gewählten Epoche in der Regel der Anfang des 1. solaren Jahres und der des 1. lunaren Monats nicht gleich sind. Insofern ist ein Anfangswert zu addieren, der hier mit R(m) bezeichnet wird.
Dabei unterscheiden sich diese Anfangswerte für die verschiedenen astronomischen Schulen Tibets, die hier mit m bezeichnet sind. Bezogen auf die Epoche des Kālacakratantra rechnet die Mehrzahl dieser Schulen mit R = 0. Die wichtigste Ausnahme ist die Phugpa-Schule (m=1), die mit dem Wert R(1) = 61 rechnet. Die Gründe hierfür ergeben sich aus den oben angeführten Überlegungen zur Errechnung der große Konjunktion.
Für die Errechnung der Zahl der vergangenen lunaren Monate L zu Beginn des Monats M ergibt sich dann folgendes:
Das Ergebnis wird als „exakte Zahl der vergangenen lunaren Monate“ (tib.: tshes zla rnam par dag pa) bezeichnet.
Für die Darstellung auf dem Sandabakus entspricht die obige Formel:
- [(J-1) · 12 + (M-1), ((J-1) · 12 + (M-1)) · 2 + R(m)]/(-,65) = [L(J,M), r(M)]/(-,65).
Die vorstehende Rechnung wird bei der Erstellung eines Kalenders nur für den Jahresanfang, also für M = 1, durchgeführt. Beim Übergang von einem Monat innerhalb eines Jahres zum nächsten Monat wiederholt man dann nicht die obige Rechnung, sondern addiert zu L(J,M) den Betrag 1 und zu r(M) den Betrag 2, rechnet also L(J,M+1) = L(J,M) + 1 und r(M+1) = r(M) + 2.
Schaltmonate
Der Rest r(M) der vorstehenden Rechnung, also , ist die Größe der Verschiebung des Anfangs des solaren Monats gegenüber dem lunaren Monat. Er wird als zla bshol rtsis ´phro „Kalkulationsrest für den Schaltmonat“ bezeichnet.
Diese Bezeichnung wurde aus folgendem Grunde gewählt: Ergibt sich r(M) = 0 oder r(M)=1, so übersteigt die Verschiebung der beiden Monatsarten gegeneinander die Länge eines Monats und der Wert L(J.M) steigt um 2 an. Dies hat zur Folge, dass die Abweichung des Jahresanfangs des Kalenders von dem des solaren Jahres größer als ein Monat ist. Um dies zu korrigieren, wird ein Schaltmonat (tib.: zla bshol oder zla lhag) hinzugefügt.
Nach Dragpa Gyeltshen (1147–1216) wurde beim Auftreten von r(M) = 0 oder r(M)=1 der vorangehende Monat doppelt gezählt. Diese vorgeordnete Einschaltung bedeutet, dass z. B. auf einen vorangehenden Sa ga-Monat, bei dem r(M) = 63 oder r(M) = 64 vorlag, ein zweiter Sa ga-Monat folgte, der dann auch als Schaltmonat angesehen wurde.
Daneben kann man den Gebrauch einer nachgeordneten Einschaltung beobachten, bei der nachfolgende Monat doppelt gezählt wurde. Auf den Sa ga-Monat, bei dem r(M) = 63 oder r(M) = 64 vorlag, folgte dann ein 1. und ein 2. sNron-Monat, wobei der 1. sNron-Monat der Schaltmonat war.
Des Weiteren kann man den Gebrauch beobachten, dass alternierend bei r(M)=0 der Schaltmonat dem vorhergehenden Monat zugeordnet wurde und bei r(M) = 1 der Schaltmonat dem gerade in Rechnung stehenden Monat vorangestellt bzw. zugeordnet wurde.
Eine folgenschwere Änderung der Errechnung der Schaltmonate wurde durch die Phugpa-Schule dadurch hervorgerufen, dass diese Schule rückgerechnet auf die Epoche des Kālacakratantra (Jahresbeginn im Jahre 806) den Anfangswert zur Umrechnung der vergangenen solaren Monate in synodische Monate von 0 auf 61 änderte. Dies hatte zur Folge, dass die Einfügung von Schaltmonaten im Vergleich zur vorstehend beschriebenen Methode drei Monate später stattfand. Natürlich ist nicht auszuschließen, dass hierzu sowohl eine nachgeordnete, vorgeordnete als auch alternierende Zählung der Schaltmonate gelegentlich in Gebrauch war.
Eine weitere radikale Änderung der Berechnung von Schaltmonaten fand im 17. Jahrhundert statt. Bei dieser neuen Methode orientierte man sich nunmehr an der Berechnung der sogenannten Ch´i-Zentren (tib.: sgang) der chinesischen Astronomie. Diese neue Schaltmethode wurde im Verwaltungsbereich der zentraltibetischen Regierung im Jahre 1696 nach dem Tod des 5. Dalai Lama eingeführt und wird auch heute noch verwendet.
Der Wochentag für den Beginn des mittleren lunaren Monats M (gza' yi dhru va)
Das Ziel dieser Berechnung ist die Ermittlung des Wochentages für den Beginn des mittleren lunaren Monats M.
Der der Verkündung durch den Buddha zugeschriebene Umrechnungswert von mittlerem lunaren Tag in die Zeitgröße natürlicher Tag wird mit
angegeben. Multipliziert man 30 (lunare Tage) mit B, so erhält man als Länge eines lunaren Monats in natürlichen Tagen den Betrag
- [29,31,50, 0, 480]/(-,60,60,6,707) d.
Der 28d, also der 4 ganze Wochen, übersteigende Betrag ist somit:
- W(1,1) = [1,31,50, 0, 480]/(7,60,60,6,707) d.
Um nun den Wochentag zu ermitteln, in dem der lunare Monat M beginnt, ist noch zu beachten, dass die Epoche in der Regel nicht mit dem Wochentag 0 beginnt. Insofern ist ein Anfangswert WA(m) zu berücksichtigen.
Wie man aus der folgenden Tabelle entnehmen kann, verwenden die bisher bekannt gewordenen verschiedenen tibetischen Schulen der Astronomie für W und WA und auch für R teilweise unterschiedliche Werte. Alle Anfangswerte beziehen sich auf die Epoche des Kālacakratantra.
Tabelle 1:
| Schule | W(m,1): 28d übersteigender Betrag der Länge
eines mittleren lunaren Monats |
W(m,2): Beim Übergang von einem Monat zum nächsten zu addierender Wert für den Wochentag | WA(m): Anfangswerte für den Wochentag | R(m): Anfangswerte für
den lunaren Monat |
|---|---|---|---|---|
| m=1: Phugpa-Schule | W(1,1) = [1,31,50,0,480]/(7,60,60,6,707) | W(1,2) = [1,31,50,0,480]/(7,60,60,6,707) | WA(1) = [0,50,44,2,38]/(7,60,60,6,707) | R(1)=61 |
| m=2: Sogenannte exakte byed rtsis | W(2,1) = [1,31,50]/(7,60,60) | W(2,2) = [1,31,50]/(7,60,60) | WA(2) = [2,30,0]/(7,60,60) | R(2)=0 |
| m=3: Kalenderrechnung des Kālacakratantra | W(3,1) = [1,31,50]/(7,60,60) | W(3,2) = [1,32,0]/(7,60,60) | WA(3) = [2,30,0]/(7,60,60) | R(3)=0 |
| m=4: Kalenderrechnung des Chögyel Phagpa | W(4,1) = [1,31,50]/(7,60,60) | W(4,2) = [1,31,50]/(7,60,60) | WA(4) = [2,30,0]/(7,60,60) | R(4)=0 |
| m=5: Kalenderrechnung des Kālacakrāvatāra | W(5,1) = [1,31,50]/(7,60,60) | W(5,2) = [1,32,0]/(7,60,60) | WA(5) = [2,30,0]/(7,60,60) | R(5)=0 |
| m=6: 1. abweichende Kalenderrechnung des Kālacakrāvatāra | W(6,1) = [1,31,50]/(7,60,60) | W(6,2) = [1,32,0]/(7,60,60) | WA(6) = [2,30,0]/(7,60,60) | R(6)=0 |
| m=7: 2. abweichende Kalenderrechnung des Kālacakrāvatāra | W(7,1) = [1,31,50]/(7,60,60) | W(7,2) = [1,32,0]/(7,60,60) | WA(7) = [2,30,0]/(7,60,60) | R(7)=0 |
| m=8: Kalenderrechnung der Tshurphu-Schule | W(8,1) = [1,31,50,0,480]/(7,60,60,6,707) | W(8,2) = [1,31,50,0,480]/(7,60,60,6,707) | WA(8) = [2,25,20,2,352]/(7,60,60,6,707) | R(8)=0 |
| m=9: Kalenderrechnung des Jamgön Kongtrül Lodrö Thaye | W(9,1) = [1,31,50,0,30]/(7,60,60,6,44) | W(9,2) = [1,31,50,0,30]/(7,60,60,6,44) | WA(9) = [2,21,43,5,2]/(7,60,60,6,44) | R(9)=0 |
| m=10: Neue Kalenderrechnung des Klosters Ganden | W(10,1) = [1,31,50,0,480]/(7,60,60,6,707) | W(10,2) = [1,31,50,0,480]/(7,60,60,6,707) | WA(10) = [2,26,50,4,352]/(7,60,60,6,707) | R(10)=0 |
Multipliziert man nun den Betrag W(m,1) mit der Zahl der vergangenen lunaren Monate L(J,M) und addiert den Anfangswert WA(m), so erhält man bei Weglassung der ganzzahligen Vielfachen von 7 (mod 7) den gesuchten mittleren Wochentag und die Tageszeit, für den Beginn des Monats M, bzw. wenn M = 1 ist, für den Beginn des Jahres, nach der Kalenderrechnung m.
- .
Dieser Wert wird im Tibetischen als gza' yi dhru va bezeichnet.
Beim Übergang von einem Monat zum anderen wiederholt man nicht die gesamte Rechnung, sondern addiert zu den in der vorstehenden Tabelle 1 verzeichneten Betrag W(m,2), ein Wert, der sich eigentlich von W(m,1) nicht unterscheiden sollte, der aber aus Gründen der Aufrundung bei einigen Kalenderrechnungen davon verschieden ist. Für die Erstellung eines Kalenders läuft diese Rechnung auf
hinaus.
Die Ergebnisse und unterscheiden sich für die Kalenderrechnungen m = 1, 2, 4, 8, 9 und 10 nicht. Bei allen anderen Kalenderrechnungen ist die Rechnung nach durchzuführen.
Übergang zum mittleren lunaren Tag (gza' yi bar ba)

Da ein lunarer Monat aus 30 lunaren Tagen (tshes zhag) besteht, dividiert man die Länge eines lunaren Monats in d durch 30, also z. B. für die Phugpa-Schule
- W(1;3) = (28 + W(1,1)):30 = [0,59,3,4,16]/(7,60,60,6,707),
und erhält die Länge eines lunaren Tages in natürlichen Tagen d.
Aus Gründen der Vereinfachung der weiteren Rechnung verwenden nicht alle Kalenderrechnungen diesen Wert der Phugpa-Schule, wie die folgende Tabelle zeigt.
Tabelle 2, Zeitliche Länge eines mittleren lunaren Tages in natürlichen Tagen d:
| Schule | W(m,3): Zeitliche Länge eines mittleren lunaren Tages in d |
|---|---|
| m=1: Phugpa-Schule | W(1,3) = [0,59,3,4,16]/ (7,60,60,6,707) |
| m=2: Sogenannte exakte byed rtsis | W(2,3) = [0,59,3,4]/(7,60,60,6) |
| m=3: Kalenderrechnung des Kālacakratantra | W(3,3) = [0,59]/(7,60) |
| m=4: Kalenderrechnung des Chögyel Phagpa | W(4,3) = [0,59]/(7,60) |
| m=5: Kalenderrechnung des Kālacakrāvatāra | W(5,3) = [0,59]/(7,60) |
| m=6: 1. abweichende Kalenderrechnung des Kālacakrāvatāra | W(6,3) = [0,59]/(7,60) |
| m=7: 2. abweichende Kalenderrechnung des Kālacakrāvatāra | W(7,3) = [0,59]/(7,60) |
| m=8: Kalenderrechnung der Tshurphu-Schule | W(8,3) = [0,59,3,4,16]/(7,60,60,6,707) |
| m=9: Kalenderrechnung des Jamgön Kongtrül Lodrö Thaye | W(9,3) = [0,59,3,4,1]/(7,60,60,6,44) |
| m=10: Neue Kalenderrechnung des Klosters Ganden | W(10,3) = [0,59,3,4,16]/(7,60,60,6,707) |
Zur Berechnung des Wochentages und der Tageszeit für das Ende des lunaren Tages T multipliziert man nun W(m,3) mit T und addiert das Ergebnis zu , rechnet also
- .
Das Ergebnis wird im Tibetischen gza' yi bar ba genannt. Es gibt Wochentag und Tageszeit für das Ende des mittleren lunaren Tages T im Monat M des Jahres J.
Um die sich die Rechnung T · W(m,3) zu ersparen, enthalten neuere tibetische Lehrbücher der Astronomie Tabellen, in denen man das Ergebnis dieser Multiplikation unmittelbar ablesen kann.
Berechnung der mittleren ekliptikalen Länge der Sonne
Die Aufgabenstellung ist die Berechnung der mittleren ekliptikalen Länge der Sonne SO(m,T) am Ende des lunaren Tages T nach der Kalenderrechnung m. Winkelmaß für die Bestimmung der Länge bilden die Einteilung der Ekliptik in Mondhäuser und deren Unterteilung. Da man diese Aufgabenstellung analog zur Berechnung von WO(m,T) durchführt, benötigt man folgende Größen für die verschiedenen Kalenderrechnungen m:
- Veränderung der mittleren Länge der Sonne pro lunarem Monat:S(m,1),
- Veränderung der mittleren Länge der Sonne pro lunarem Monat beim Übergang von einem Monat zum folgenden Monat: S(m,2),
- Veränderung der mittleren Länge der Sonne pro lunarem Tag: S(m,3),
- Den Anfangswert der ekliptikalen Länge der Sonne zur Epoche: SA(m).
Grundsätzlich lassen sich diese Werte, abgesehen vom Anfangswert, mit den Umrechnungsfaktoren A und B rein rechnerisch ermitteln. Dem folgt auch die Phugpa-Schule, aber die Werte der andern Schulen weichen aus unterschiedlichen Gründen hiervon ab.
Tabelle 3:
| Schule | S(m,1): Veränderung der Länge der Sonne pro lunarem Monat | S(m,2): Beim Übergang von einem Monat zum nächsten zu addierender Wert für die Veränderung der Länge der Sonne | S(m,3): Veränderung der Länge der Sonne pro lunarem Tag | SA(m): Anfangswerte für die Länge der Sonne |
|---|---|---|---|---|
| m=1: Phugpa-Schule | S(1,1) = [2,10,58,1,17]/(27,60,60,6,67) | S(1,2) = [2,10,58,1,17]/(27,60,60,6,67) | S(1,3) = [0,4,21,5,43]/(7,60,60,6,707) | SA(1) = [24,57,5,2,16]/(7,60,60,6,707) |
| m=2: Sogenannte exakte byed rtsis | S(2,1) = [2,10,58,2,10]/(27,60,60,6,13) | S(2,2) = [2,10,58,2,10]/(27,60,60,6,13) | S(2,3) = [0,4,21,5,9]/(27,60,60,6,13) | SA(2) = [26,58]/(27,60) |
| m=3: Kalenderrechnung des Kālacakratantra | S(3,1) = [2,10,58,2,10]/(27,60,60,6,13) | S(3,2) = [2,11]/(27,60) | S(3,3) = [0,4,20]/(7,60,60) | SA(3) = [26,58]/(27,60) |
| m=4: Kalenderrechnung des Chögyel Phagpa | S(4,1) = [2,10,58,2,10]/(27,60,60,6,13) | S(4,2) = [2,11]/(27,60) | S(4,3) = [0,4,26]/(7,60,60) | SA(4) = [26,58]/(27,60) |
| m=5: Kalenderrechnung des Kālacakrāvatāra | S(5,1) = [2,10,58,2,10]/(27,60,60,6,13) | S(5,2) = [2,11]/(27,60) | S(5,3) = [0,4,20]/(7,60,60) | SA(5) = [26,58]/(27,60) |
| m=6: 1. abweichende Kalenderrechnung des Kālacakrāvatāra | S(6,1) = [2,10,58,2,10]/(27,60,60,6,13) | S(6,2) = [2,11]/(27,60) | S(6,3) = [0,4,26]/(7,60,60) | SA(6) = [26,58]/(27,60) |
| m=7: 2. abweichende Kalenderrechnung des Kālacakrāvatāra | S(7,1) = [2,10,58,2,10]/(27,60,60,6,13) | S(7,2) = [2,11]/(27,60) | S(7,3) = [0,4,22]/(7,60,60) | SA(7) = [26,58]/(27,60) |
| m=8: Kalenderrechnung der Tshurphu-Schule | S(8,1) = [2,10,58,1,17]/(27,60,60,6,67) | S(8,2) = [2,10,58,1,17]/(27,60,60,6,67) | S(8,3) = [0,4,21,5,43]/(7,60,60,6,67) | SA(8) = [0,29,34,5,37]/(7,60,60,6,67) |
| m=9: Kalenderrechnung des Jamgön Kongtrül Lodrö Thaye | S(9,1) = [2,10,58,2,20]/(27,60,60,6,38) | S(9,2) = [2,10,58,2,20]/(27,60,60,6,38) | S(9,3) = [0,4,21,5,26]/(7,60,60,6,38) | SA(9) = [0,1,54,4,22]/(7,60,60,6,38) |
| m=10: Neue Kalenderrechnung des Klosters Ganden | S(10,1) = [2,10,58,2,500]/(27,60,60,6,707) | S(10,2) = [2,10,58,2,500]/(27,60,60,6,707) | S(10,3) = [0,4,21,5,488]/(27,60,60,6,707) | SA(10) = [0,18,0,0,135]/(27,60,60,6,707) |
Die mittlere Länge der Sonne für den Beginn des mittleren lunaren Monats M (tib.: nyi ma'i dhru va) errechnet sich somit mit
- .
Dies gilt generell nur für den Jahresanfang, da einige Kalenderrechnung beim Übergang von einem Monat zum nächsten teilweise verkürzte Werte S(m,2) addieren. Insofern ist allgemein mit
zu rechnen.
Zur Berechnung der Länge der mittleren Sonne am Ende des mittleren lunaren Tages T multipliziert man T mit S(m,3) und addiert das Ergebnis zu SO(m,M):
- .
Dies ist die mittlere ekliptikale Länge der Sonne am Ende des mittleren lunaren Tages T (tib.: nyi ma'i bar ba) nach der Kalenderrechnung m.
Die Füße des Mondes und der Sonne: Mittelpunktsgleichungen von Mond und Sonne
Da sich der Mond nicht auf einer Kreisbahn, sondern annähernd auf einer Ellipse um die Erde bewegt, variiert seine Winkelgeschwindigkeit. Am Punkt der größten Erdentfernung ist seine Winkelgeschwindigkeit am kleinsten und am Punkt der größten Erdnähe am größten. Das Gleiche gilt für die scheinbare Sonnenbahn.
Diese unterschiedlichen Winkelgeschwindigkeiten führen dazu, dass die beobachteten ekliptikalen Längen beider Himmelskörper von den berechneten mittleren Längen abweichen. Die mathematische Formel, mit der man diese Abweichung von der mittleren Länge berechnet, nennt man Mittelpunktsgleichung. In der graphischen Darstellung ergibt sich aus dieser Gleichung eine trigonometrische Kurve.
In der tibetischen Astronomie wird diese Abweichung auf dem Sandabakus mit Systemen von linearen Gleichungen berechnet, die Füße des Mondes (tib.: zla ba'i rkang pa) oder Füße der Sonne (tib.: nyi ma'i rkang pa) genannt werden.
Für die tibetische Kalenderrechnung spielen die Mittelpunktsgleichungen im Zusammenhang mit der Länge eines lunaren Tages insofern eine Rolle, als dieser als die Zeitspanne definiert ist, die benötigt wird, um den Winkelabstand zwischen Sonne und Mond um 12 Grad zu vergrößern. Bewegt sich nun der Mond langsamer als im Mittel, wird diese benötigte Zeitspanne im Vergleich zur mittleren Länge entsprechend größer. Bewegt sich die Sonne schneller, resultiert daraus das Gleiche. Mit den Mittelpunktsgleichungen von Mond und Sonne ist es daher möglich, die Verlängerung oder Verkürzung der Zeitdauer eines lunaren Tages im Vergleich zum Mittel aufgrund der Unregelmäßigkeit der Mond- und Sonnenbewegung zu berechnen.
Voraussetzung für die Rechnung mit einer Mittelpunktsgleichung ist die Bestimmung der mittleren Länge eines Himmelskörpers im sogenannten anomalistischen Umlauf, bei dem der Nullpunkt des Winkelabstands in der tibetischen Astronomie nicht mit dem erdfernsten oder erdnahesten Punkt, sondern mit dem Punkt zusammenfällt, bei dem die Abweichung von der mittleren Winkelgeschwindigkeit gleich 0 ist. Zudem ist dieser Punkt bei Sonne und Mond so festgelegt, dass sich beide Himmelskörper von hier aus auf den erdfernsten Punkt zubewegen.
Die Füße des Mondes

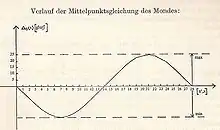
Für den Mond teilt man dabei den vollen anomalistischen Umlauf in 28 Teile, die ril po genannt werden. Diese Teile wiederum werden in 126 cha-shas unterteilt. Für die Sonne und die übrigen fünf Planeten erfolgt eine Unterteilung des anomalistischen Umlaufs in 12 Teile. Der Winkelabstand des Mondes in der sogenannten Anomalie vom Nullpunkt des anomalistischen Umlaufs zu einem bestimmten Zeitpunkt wird also mit
dargestellt, wobei und Ganze Zahlen sind. Dabei wird als Größenordnung ril po bezeichnet und ist kleiner als 28, wird als Größenordnung cha shas genannt und ist kleiner als 126.
Ziel der Rechnung ist zunächst die Berechnung des Winkelabstands des Mondes von Nullpunkt der Anomalie am Ende des mittleren lunaren Tages T des Monats M im Jahr J seit Epoche.
Die Berechnung dieses anomalistischen Winkels wird analog zur Berechnung der ekliptikalen Länge der Sonne durchgeführt. Dazu benötigt man folgende Angaben:
- Veränderung des Winkelabstands des Mondes pro lunarem Monat mod 28: AN(m,1),
- Veränderung des Winkelabstands des Mondes in der Anomalie beim Übergang von einem Monat zum folgenden Monat: AN(m,2),
- Veränderung des Winkelabstands des Mondes in der Anomalie pro lunarem Tag: AN(m,3),
- Den Anfangswert des Winkelabstands des Mondes zur Epoche: ANA(m).
Tabelle 3:
| Schule | AN(m,1): Veränderung des Winkelabstands des Mondes in der Anomalie pro lunarem Monat mod 28 | AN(m,2): Veränderung des Winkelabstands des Mondes in der Anomalie beim Übergang von einem Monat zum folgenden Monat | AN(m,3): Veränderung des Winkelabstands des Mondes in der Anomalie pro lunarem Tag | ANA(m): Anfangswerte des Winkelabstands des Mondes in der Anomalie |
|---|---|---|---|---|
| m=1: Phugpa-Schule | AN(1,1) = [2,1]/(28,126) | AN(1,2) = [2,1]/(28,126) | AN(1,3) = [1,0]/(28,126) | ANA(1) = [3,97]/(28,126) |
| m=2: Sogenannte exakte byed rtsis | AN(2,1) = [2,1]/(28,126) | AN(2,2) = [2,1]/(28,126) | AN(2,3) = [1,0]/(28,126) | ANA(2) = [5,112]/(28,126) |
| m=3: Kalenderrechnung des Kālacakratantra | AN(3,1) = [2,1]/(28,126) | AN(3,2) = [2,0]/(28,126) | AN(3,3) = [1,0]/(28,126) | ANA(3) = [5,112]/(28,126) |
| m=4: Kalenderrechnung des Chögyel Phagpa | AN(4,1) = [2,1]/(28,126) | AN(4,2) = [2,1]/(28,126) | AN(4,3) = [1,0]/(28,126) | ANA(4) = [5,112]/(28,126) |
| m=5: Kalenderrechnung des Kālacakrāvatāra | AN(5,1) = [2,1,]/(28,126) | AN(5,2) = [2,1]/(28,126) | AN(5,3) = [1,0]/(28,126) | ANA(5) = [5,112]/(28,126) |
| m=6: 1. abweichende Kalenderrechnung des Kālacakrāvatāra | AN(6,1) = [2,1,]/(28,126) | AN(6,2) = [2,0]/(28,126) | AN(6,3) = [1,0]/(28,126) | ANA(6) = [5,112]/(28,126) |
| m=7: 2. abweichende Kalenderrechnung des Kālacakrāvatāra | AN(7,1) = [2,1,]/(28,126) | AN(7,2) = [2,0]/(28,126) | AN(7,3) = [1,0]/(28,126) | ANA(7) = [5,112]/(28,126) |
| m=8: Kalenderrechnung der Tshurphu-Schule | AN(8,1) = [2,1,]/(28,126) | AN(8,2) = [2,1]/(28,126) | AN(8,3) = [1,0]/(28,126) | ANA(8) = [5,112]/(28,126) |
| m=9: Kalenderrechnung des Jamgön Kongtrül Lodrö Thaye | AN(9,1) = [2,1,]/(28,126) | AN(9,2) = [2,1]/(28,126) | AN(9,3) = [1,0]/(28,126) | ANA(9) = [5,112]/(28,126) |
| m=10: Neue Kalenderrechnung des Klosters Ganden | AN(10,1) = [2,1,]/(28,126) | AN(10,2) = [2,1]/(28,126) | AN(10,3) = [1,0]/(28,126) | ANA(10) = [5,112]/(28,126) |
Der Winkelabstand des Mondes im anomalistischen Umlauf für den Beginn des mittleren lunaren Monats M (tib.: ril cha) errechnet sich somit mit
- .
Dies gilt generell nur für den Jahresanfang, da einige Kalenderrechnung beim Übergang von einem Monat zum nächsten teilweise verkürzte Werte AN(m,2) addieren. Insofern ist allgemein mit
zu rechnen.
Zur Berechnung des Winkelabstands des Mondes am Ende des mittleren lunaren Tages T addiert man T, da für alle m AN(m,3) = 1 ist, und addiert das Ergebnis zu :
- .
Dies ist der Winkelabstand des Mondes im anomalistischen Umlauf am Ende des mittleren lunaren Tages T nach der Kalenderrechnung m.
Die aus der Beobachtung resultierenden Abweichungen der tatsächlichen Länge des Mondes von der mittleren Länge sind nun in der tibetischen Astronomie mit einer Tabelle erfasst, die für jedes ril po die Abweichung am Anfang dieses Winkelabschnitts verzeichnet und die Veränderung der Abweichung innerhalb der Winkelmaßeinheit ril po notiert.
Diese Tafel wird im Tibetischen mit zla rkang re'u mig „Tafel der Füße des Mondes“ bezeichnet, wobei die Füße des Mondes (zla ba'i rkang pa) einzelne Rechenvorschriften bezeichnen, die letztendlich lineare Gleichungen sind. Da die Abweichungen innerhalb eines vollen anomalistischen Umlaufs für jeweils 180 Grad symmetrisch sind, verzeichnet man in der Tafel nur 14 Werte, da die folgenden 14 Werte abgesehen vom Vorzeichen gleich sind. Für die Benutzung der Tafel errechnet man deshalb den Winkelabstand für jeweils einen halben anomalistischen Umlauf:
- A(m,T) = ( + T ) mod 14
- = [n,x]/(14,126) .
Dabei ist der Wert
zu notieren, da er darüber entscheidet, ob die mit den Mittelpunktsgleichungen errechneten Werte zu addieren oder subtrahieren sind.
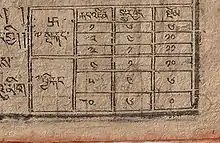
Tafel für die Mittelpunktsgleichungen des Mondes:
| n: Zugriffsnummern der Gleichungen (tib.: rkang ´dzin) | : Steigung der Funktion oder Multiplikator (tib.: sgyur byed) | : Anfangswerte der Funktionen (tib.: rkang sdom) | |
|---|---|---|---|
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 1 | 5 | 5 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 2 | 5 | 10 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 3 | 5 | 15 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 4 | 4 | 19 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 5 | 3 | 22 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 6 | 2 | 24 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 7 | 1 | 25 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 8 | -1 | 24 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 9 | -2 | 22 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 10 | -3 | 19 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 11 | -4 | 15 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 12 | -5 | 10 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 13 | -5 | 5 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 0 | -5 | 0 |
Grundsätzlich berechnet man in der Tibetischen Kalenderrechnung anhand der Mittelpunktsgleichungen die Änderung der Länge des lunaren Tages, die sich durch die Abweichung der tatsächlichen Winkelgeschwindigkeit des Mondes von der mittleren Geschwindigkeit ergibt. Bewegt sich der Mond langsamer als im Mittel, werden die lunaren Tage länger. Bewegt er sich schneller als im Mittel, werden die lunaren Tage kürzer.
Die im Folgenden zu berechnenden Beträge ergeben hierbei die Verlängerung oder Verkürzung der Zeitdauer eines lunaren Tages im Vergleich zum Mittel aufgrund der Unregelmäßigkeit der Mondbewegung. Da für x=0 sich ergibt, bedeutet dies, dass Nullpunkt des Winkelabstands in der Anomalie in der tibetischen Astronomie nicht mit dem erdfernsten oder erdnahesten Punkt, sondern mit dem Punkt zusammenfällt, bei dem die Abweichung von der mittleren Winkelgeschwindigkeit gleich 0 ist. Da nach Durchlaufen dieses Punktes die lunaren Tage zeitlich länger werden, bedeutet dies, dass sich der Mond langsamer wird, sich also in Richtung des erdfernsten Punktes (Apogäum) bewegt und diesen mit dem Beginn des 8. ril po erreicht. Der erdnaheste Punkt (Perigäum) fällt mit dem Beginn des 22. ril po zusammen.
Anhand der Tafel der Mittelpunktsgleichungen errechnet sich die Korrekturgröße für die Länge eines mittleren lunaren Tages mit der folgenden Gleichung:
- .
Dieser Betrag wird zu WO(m,T), also dem zu dem Wert für den Wochentag und die Tageszeit für das Ende des mittleren lunaren Tages T im Monat M des Jahres J, addiert, falls das Ergebnis von
die Zahl 0 oder 2 ergeben hat. Ergab das Ergebnis dieser Rechnung die Zahl 1, wird der Betrag subtrahiert.
Das Ergebnis wird im Tibetischen als gza' phyed dag pa „halbkorrekter Wochentag für das Ende des lunaren Tages“ bezeichnet. Die Bezeichnung „halbkorrekt“ wird deshalb gebraucht, weil eine durch die Unregelmäßigkeit der Sonnenbewegung bedingte Korrekturgröße noch nicht berücksichtigt wurde.
Die Füße der Sonne
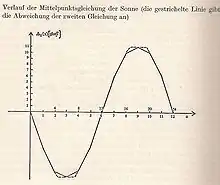
Für die Berechnung der Mittelpunktsgleichung der Sonne wird der scheinbare anomalistische Umlauf der Sonne in 12 Teile geteilt, was im Winkelmaß der Einteilung in die zwölf Tierkreiszeichen entspricht. Allerdings ist der Nullpunkt des anomalistischen Umlaufs gegenüber dem Nullpunkt der Winkelmaße der Tierkreiszeichen bzw. der Mondhäuser um 90 Grad verschoben.
Wie beim Mond fällt der Nullpunkt des Winkelabstands im anomalistischen Umlauf der Sonne in der tibetischen Astronomie nicht mit dem erdfernsten oder erdnahesten Punkt, sondern mit dem Punkt zusammen, bei dem die Abweichung von der mittleren Winkelgeschwindigkeit gleich 0 ist. Da nach Durchlaufen dieses Punktes die Beträge aus den Mittelpunktsgleichungen zur Länge der mittleren Sonne zu subtrahieren sind, folgt, dass die Winkelgeschwindigkeit der Sonne kleiner wird, sie sich also in Richtung des erdfernsten Punktes (Aphel) bewegt. Dieser fällt mit dem Nullpunkt des Umlaufs in den Tierkreiszeichen und den Mondhäusern zusammen.
Die Abweichungen der der Winkelgeschwindigkeiten der Sonne von der mittleren Geschwindigkeit werden wie beim Mond durch eine Tabelle dargestellt, zu der eine entsprechende Rechenvorschrift gehört.
Diese Tafel wird im Tibetischen mit nyi rkang re'u mig „Tafel der Füße des Sonne“ bezeichnet, wobei die Füße der Sonne (nyi ma'i rkang pa) einzelne Rechenvorschriften bezeichnen, die letztendlich lineare Gleichungen sind. Da die Abweichungen innerhalb eines vollen anomalistischen Umlaufs für jeweils 180 Grad symmetrisch sind, verzeichnet man in der Tafel nur 6 Werte, da die folgenden 6 Werte abgesehen vom Vorzeichen gleich sind. Für die Benutzung der Tafel errechnet man deshalb den Winkelabstand für jeweils einen halben anomalistischen Umlauf.
Ausgangspunkt der Rechnung ist SO(m,T) also ist die mittlere ekliptikale Länge der Sonne am Ende des mittleren lunaren Tages T (tib.: nyi ma'i bar ba) nach der Kalenderrechnung m. Es ist noch einmal zu betonen, dass die Winkelmaßeinheit dieser Größe in Mondhäuser angegeben ist, dem Winkelmaß also die Einteilung der Ekliptik in 27 Teile zugrunde liegt.
Der Wert SO(m,T) wird zunächst um [6,45]/(27,60) = 90 Grad reduziert:
- = SO(m,T) – [6,45]/(27,60).
Damit hat man die Größenangabe auf den Nullpunkt des anomalistischen Umlaufs umgestellt. Ist das Ergebnis größer als [13,30]/(27,60) oder gleich diesem Wert, zieht man den diesen Wert für einen halben Umlauf (= [13,30]/(27,60)) ab. Man notiert, ob dieser Wert abgezogen wurde oder nicht. Das Ergebnis sei mit
bezeichnet. Um nun auf die Mittelpunktsgleichungen der Sonne zugreifen zu können, berechnet man die Nummer der jeweiligen Gleichung mit
- .
Zum Verständnis dieser Rechnung ist zu beachten, dass 12 Tierkreiszeichen 27 Mondhäuser entsprechen. Der Umrechnungsfaktor zwischen diesen Winkelmaßen ist somit
- .
Die Größe der Variablen x in diesen Mittelpunktsgleichungen ergibt sich mit:
- .
Tafel für die Mittelpunktsgleichungen der Sonne:
| n: Zugriffsnummern der Gleichungen (tib.: rkang ´dzin) | : Steigung der Funktion oder Multiplikator (tib.: sgyur byed) | : Anfangswerte der Funktionen (tib.: rkang sdom) | |
|---|---|---|---|
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 1 | 6 | 6 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 2 | 4 | 10 |
| Erste Hälfte der Gleichungen (tib.: snga rkang): Zu addierende Beträge. | 3 | 1 | 11 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 4 | -1 | 10 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 5 | -4 | 6 |
| Zweite Hälfte der Gleichungen (tib.: phyi rkang): Zu subtrahierende Beträge. | 6 | -6 | 0 |
Anhand dieser Tafel der Mittelpunktsgleichungen errechnet sich die Korrekturgröße für die mittlere ekliptikale Länge der Sonne mit der folgenden Gleichung:
- .
Korrekte ekliptikale Länge der Sonne
Zur Berechnung der ekliptikalen Länge der Sonne am Ende des lunaren Tages T subtrahiert man von SO(m,T) den Betrag , wenn der Betrag SO(m,T) – [6,45]/(27,60) nicht um einen halben Umlauf zu reduzieren war. Anderenfalls wird zu SO(m,T) addiert. Das Ergebnis, die exakte ekliptikale Länge der Sonne am Ende des lunaren Tages T, wird Tibetisch als nyi ma dag pa bezeichnet.
Korrektes Ende des lunaren Tages
Zur Berechnung des genauen Zeitpunkts, an dem der lunaren Tag T in einem bestimmten Wochentag endet, subtrahiert man vom berechneten „halbkorrekten Wochentag für das Ende des lunaren Tages“ (tib.: gza´ phyed dag pa) ebenfalls den Betrag , wenn der Betrag SO(m,T) – [6,45]/(27,60) nicht um einen halben Umlauf zu reduzieren war. Anderenfalls wird dieser Betrag addiert. Dabei ignoriert man den Fehler, der dadurch entsteht, dass es sich bei um ein Bogenmaß handelt.
Das Ergebnis wird Tibetisch gza'-dag „exakter Wochentag für das Ende des lunaren Tages“ genannt. Der mit gza'-dag bezeichnete Betrag gibt den Wochentag und die Tageszeit an, zu der der lunare Tag T endet.
Damit ist die Datumszahl T genau festgelegt, mit der ein Wochentag innerhalb eines Monats gezählt wird.
Ekliptikale Länge des Mondes
Zur Berechnung der ekliptikalen Länge des Mondes geht man von dem mittleren Winkelabstand aus, den der Mond relativ zur Sonne pro lunaren Tag zurücklegt. Für diesen wird in allen Kalenderrechnungen in Tibet der Betrag [0,54]/(27,60) Mondhäuser zugrunde gelegt. Man multipliziert diesen Betrag mit T und addiert das Ergebnis zur exakten ekliptikalen Länge der Sonne am Ende des lunaren Tages T (tib.: nyi ma dag pa). Damit hat man die ekliptikale Länge des Mondes am Ende des lunaren Tages T errechnet. Die Mittelpunktsgleichung des Mondes wird bei dieser Rechnung nicht berücksichtigt. Das Ergebnis wird Tibetisch als tshes 'khyud zla ba'i skar ma „den lunaren Tag umschlingender Sternort des Mondes“ bezeichnet.
Zieht man von diesem Wert die Tageszeit ab, zu der der lunare Tag T in dem betreffenden Wochentag endet, ergibt sich ein Betrag, der Tibetisch als res 'grogs zla ba'i skar ma „dem Wochentag zugeordneter Sternort des Mondes“ genannt wird. Dies ist die ekliptikale Länge des Mondes zu Beginn des jeweiligen Wochentages.
Die beiden astrologischen Komponenten der Kalenderrechnung
Addiert man die vorstehend berechnete Länge der Sonne und die Länge des Mondes zu Beginn des Wochentages, so erhält man eine Größe, die Sanskrit yoga (tib.: sbyor ba) genannt wird. Zahlenmäßig ergeben sich 27 Yoga-Abschnitte, die jeweils eine eigene Bezeichnung tragen.
Eine weitere nur astrologisch bedeutsame Zeitgröße wird Tibetisch als byed pa (Sanskrit: karaṇa) bezeichnet. Diese Zeitgrößen tragen ebenfalls eigene Bezeichnungen und werden wie die Yoga-Abschnitte für jeden Kalendertag in den Almanachen aufgeführt.
Immaterielles Kulturerbe
Die astronomische Kalenderrechnung der Tibeter steht auf der Liste des immateriellen Kulturerbes der Volksrepublik China (1028 X-121 Zangzu tianwen lisuan 藏族天文历算).
Literatur
- Nachum Dershowitz, Edward M. Reingold: Calendrical Calculations. Third Edition. Cambridge University Press, Cambridge u. a. 2008, ISBN 0-521-70238-0, S. 315–322.
- Winfried Petri: Indo-tibetische Astronomie. Habilitationsschrift zur Erlangung der venia legendi für das Fach Geschichte der Naturwissenschaften an der Hohen Naturwissenschaftlichen Fakultät der Ludwig-Maximilians-Universität zu München. München 1966
- Dieter Schuh: Untersuchungen zur Geschichte der Tibetischen Kalenderrechnung. Steiner, Wiesbaden 1973 (Verzeichnis der orientalischen Handschriften in Deutschland Supplement 16, ZDB-ID 538341-9).
- Dieter Schuh: Grundzüge der Entwicklung der Tibetischen Kalenderrechnung. In: Wolfgang Voigt (Hrsg.): XVIII. Deutscher Orientalistentag. Vom 1.–5. Okt. 1972 in Lübeck. Vorträge. Steiner, Wiesbaden 1974, ISBN 3-515-01860-3, S. 554–566 (Zeitschrift der Deutschen Morgenländischen Gesellschaft. Supplement 2), uni-halle.de
- Dieter Schuh (Editor): Contributions to the History of Tibetan Mathematics, Tibetan Astronomy, Tibetan Time Calculation (Calendar) and Sino-Tibetan Divination. Four Volumes. Archiv für zentralasiatische Geschichtsforschung. Herausgegeben von Dr. Karl-Heinz Everding Heft 17–20. Verlagsinformation
- Zuiho Yamaguchi: Chronological Studies in Tibet. In: Chibetto no rekigaku. Annual Report of the Zuzuki Academic foundation. X, 1973, S. 77–94.
- Zuiho Yamaguchi: The Significance of Intercalary Constants in the Tibetan Calender and Historical Tables of Intercalary Month. In: Ihara Shōren, Yamaguchi Zuihō (Hrsg.): Tibetan Studies. Proceedings of the 5th Seminar of the International Association for Tibetan Studies. Band 2: Language, history and culture. Naritasan Shinshoji, Narita-shi u. a. 1992, S. 873–895 (Monograph series of Naritasan Institute for Buddhist Studies. Occasional papers 2, 2, ZDB-ID 1225128-8).